Introduction
A sphere is a three-dimensional object which has a circular cross-section everywhere, and its volume is the space it occupies. This volume is determined by the radius of the sphere and is measured in cubic units. You can find a large number of practical examples of spherical objects, which include cricket balls, basketballs, volleyballs, and so on.
What is a Sphere
A sphere is a three-dimensional solid figure that has a round shape and every single point on the surface is equidistant from its centre. The distance between the centre and any point on the surface is known as the radius and commonly denoted by “r”. Owing to its unique shape, the sphere is one of the very few shapes in geometry that have no edges or vertices. Depending upon the way the sphere is created, we can classify it into solid sphere or a hollow sphere.
Sphere
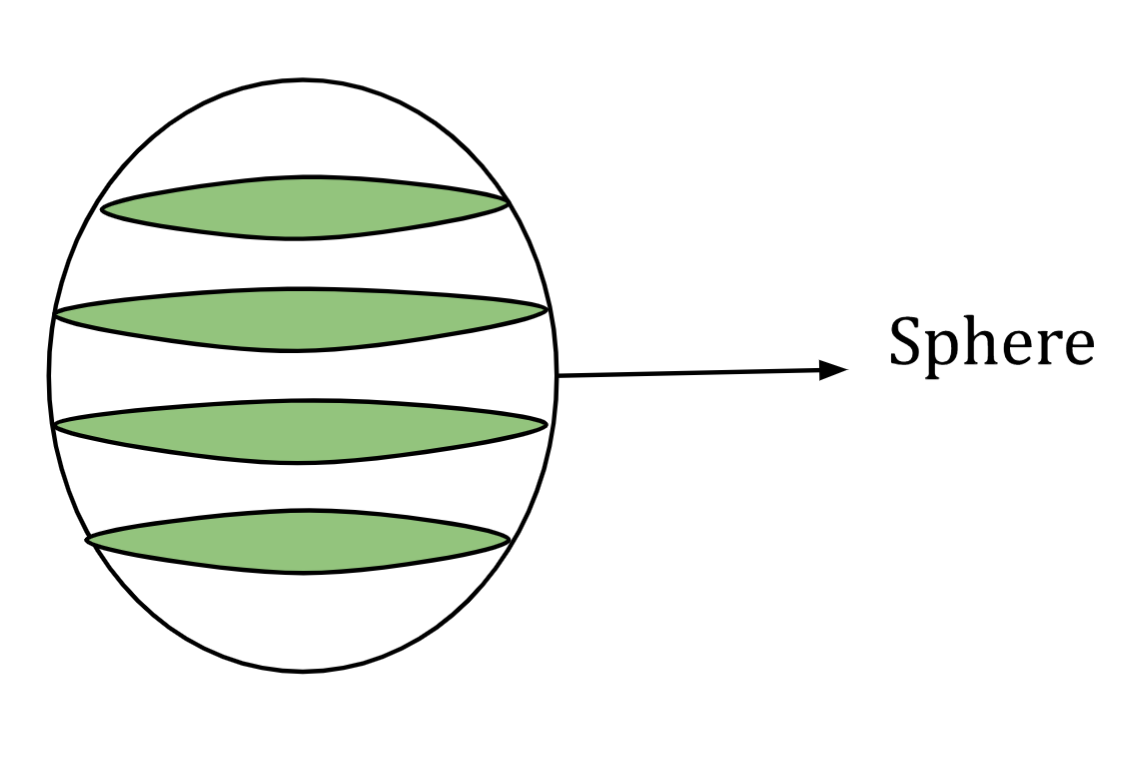
The image above shows a sphere with a few cross-sectional areas, and we can notice that when sliced in any direction, we get a circle. In fact, if viewed in two dimensions, a sphere would look just like a circle. The main difference is that a sphere is a three-dimensional figure and thus, has a specific volume. On the other hand, a circle is two-dimensional and has no volume. The figure below shows a sphere with its centre and radius marked, along with a point on its surface.
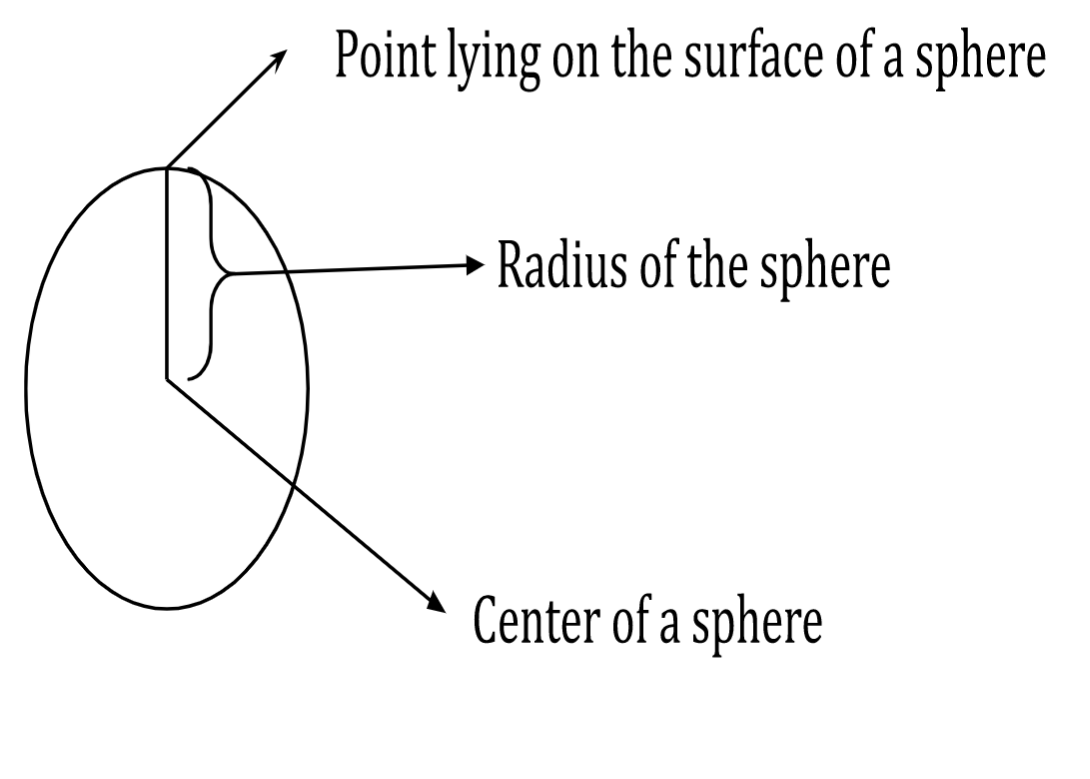
Sphere
What is the volume of a Sphere?
Solid Sphere
The sphere occupies a finite amount of space in the three-dimensional space. This is measured by its volume, and it depends upon how large the sphere is, or in other words, the radius of the sphere.
The formula for calculating the volume of a sphere is given by:
\(V = \frac{4}{3}\pi {r^3}\)
Here, r represents the radius of the sphere, which is half of its diameter. π is a universal constant whose value is approximately equal to 3.14. In terms of the diameter, we can write the volume as
\(V = \frac{1}{6}\pi {d^3}\)
The above formula also shows us that the volume of the sphere depends on the third power of the radius. This means that even a slight increase in radius will drastically increase the volume of the sphere. Mathematically, we can write that
\(V\alpha {r^3}\)
Volume of Hollow Sphere
The formula we just saw was valid for a solid sphere. However, we can also have a hollow sphere, which is a solid sphere from which, a smaller sphere has been taken out and we are left with a shell. In that case, we can simply subtract the volume of the sphere that was taken out. Let R be the outer radius of the sphere and r be the inner radius. We can then write
\((V = \frac{4}{3}\pi ({R^3} – {r^3})\)
Solved Examples
1. Calculate the volume of a sphere of radius 5 cm.
Solution
We are given that the radius is r = 5cm. The volume of a sphere is given by the formula
\(V = \frac{4}{3}\pi {r^3}\)
Hence, we have,
\(\begin{array}{l}V = \frac{4}{3} \times 3.14 \times {5^3}\\V = 523.59c{m^3}\end{array}\)
2. A hollow sphere is constructed such that its inner and outer radii are 3cm and 5cm, respectively. Find its volume.
Solution
Given that the radius of the inner sphere r = 3cm. The volume of a hollow sphere is given by the following formula:
\(V = \frac{4}{3}\pi ({R^3} – {r^3})\)
Here, R = 5 cm. Therefore, we have
\(\begin{array}{l}V = \frac{4}{3} \times 3.14 \times ({5^3} – {3^3})\\V = \frac{4}{3} \times 3.14 \times (125 – 27)\\V = \frac{4}{3} \times 307.72\\V = 410.3c{m^3}\end{array}\)
Hence, the volume of the hollow sphere \( = 410.3c{m^3}\).
Hence, the volume of the hollow sphere \( = 410.3c{m^3}\).
Word Problems
1. How much air can a spherical balloon of radius 7m hold without bursting?
Solution
Given that the radius of the sphere, r = 7m. The balloon can only hold as much air as its volume before it bursts. Thus, our job is to find its volume. We know that
\(\begin{array}{l}V = \frac{4}{3}\pi {r^3}\\V = \frac{4}{3} \times 3.14 \times {7^3}\\V = 1436.7{m^3}\end{array}\)
Thus, the balloon can hold a maximum of \(1436.7{m^3}\) of air without bursting.
Summary
This tutorial discussed the basics of sphere, and we developed an understanding of its volume by solving a few examples and word problems.
Frequently Asked Questions
1. Why isn’t it possible to calculate the volume of a circle?
A circle is a two-dimensional shape that has no defined volume. The space it occupies is given by its surface area and we have no defined volume for a circle.
2. The volume of a sphere depends on which dimensions of the sphere?
The volume of the sphere \( = \frac{4}{3}\pi {r^3}\), so the volume of a sphere depends on only the radius of the sphere. The volume of the sphere ∝ the radius of the sphere
3. Given two spheres of different radii, what would be the ratio of their volumes?
Since the volume of a sphere depends in its radius raised to the third power, the ratio of the spheres’ volumes would be equal to the ratio of the cubes of their radii. That is,
\(\frac{{{V_1}}}{{{V_2}}} = {\left( {\frac{{{r_1}}}{{{r_2}}}} \right)^3}\)