Introduction
In our daily activities, we encounter many objects of various shapes and sizes. All shapes are defined by a specific number of faces, vertices, and edges.
Cube, parallelepiped(cuboid), cone, cylinder, sphere, triangular pyramid, rectangle, and prism are examples of three-dimensional solids. A body or 3D object has three dimensions: length, width, and height. Solids have faces, edges, and vertices. As a result of these three dimensions (l, w, h), these solid shapes and objects have faces, edges, and corners.
Polyhedrons: Definition
Polyhedrons are 3D shapes with straight edges, flat faces, straight edges, and sharp vertices (corners). The word “polyhedron” comes from the Greek word, “poly” which means “many” and “polyhedron” means “area or surface”. Therefore, when many planes are joined together, they form a polyhedron. These shapes are named according to their faces, which are usually polygons. The most common names are cubes, hexahedrons, etc.
A polyhedron is a three-dimensional solid made up of polygons. It has a flat surface, straight edges, and corners. For example, a cube, prism, or pyramid is a polyhedron. Cones, spheres, and cylinders are not polyhedra because their sides are curved rather than polygonal.
Vertices
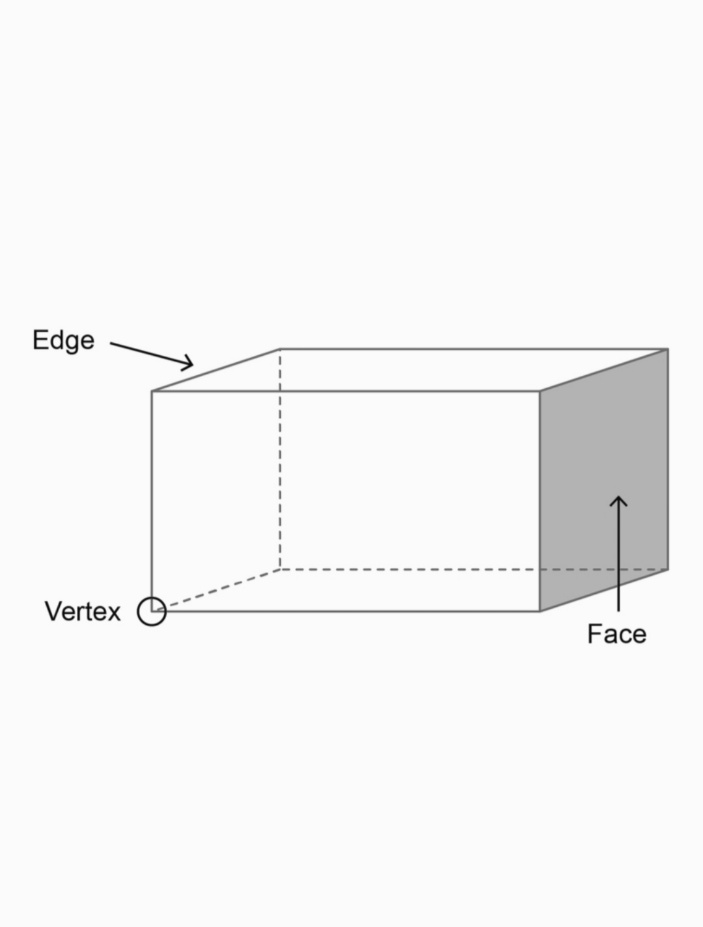
The vertices of a geometry can be defined as corners. In the other words when referring to a polygon (any straight-sided, closed 2-D figure, such as a triangle or rectangle), a vertex simply means a corner point where 2 adjacent straight lines meet. The word vertex refers to the point, not the angle.
When dealing with higher dimensions, a similar concept applies. In 3D a point wherever 2 or additional edges meet is called a vertex.
For example: Consider a rectangle: It has four vertices (plural of vertex). Because it has four corners and at every corner 2 edges meet.
Similarly,
- There are 8 vertices in the cube and cuboid.
- One vertex in the cone
- Spheres and Cylinders haven’t any vertex because their surface is curved.
Edges
The line segment between the faces is called an edge. For solid shapes, a line section wherever 2 faces meet is understood as an edge. For a polygonal shape, we will say that an edge may be a line section on the boundary connecting one vertex (corner point) to a different.
For example, a pentagon has five edges.
The line segments that type the skeleton of the 3D shapes square measure are referred to as edges.
Faces
A flat surface is called a face. In the others words A face is a single surface of a solid body. For example, a tetrahedron has four faces.
Number of Vertices, Edges, and Faces in commonly known polyhedrons
Counting Faces: To count the number of faces, we have to find the number of flat sides.
Now, number of faces in the following shapes are:
Cube = 6
Cuboid = 6
Cylinder = 3
Cone = 2
Sphere = 1
Counting Edges: To count the number of edges, we have to find the number of the line segment between the faces.
Number of edges in the following shapes are:
Cube = 12
Cuboid = 12
Cylinder = 2
Cone = 1
Sphere = 0
Counting Vertices: To count the number of vertices, we have to find the number of corners.
Number of vertices in the following shapes are:
Cube = 8
Cuboid = 8
Cylinder = 0
Cone = 1
Sphere = 0
Euler’s Formula
Now from the above topics we get the concept of faces ,edges and vertices and now we will know about Euler’s formula for polyhedra that usually deals with shapes known as solid shapes. This formula specifies the relationships between faces, edges, and vertices.
Euler’s formula can be expressed as:
F + V- E = 2
Where, F denotes the number of faces, V denotes the number of vertices, and E denotes the number of edges.
For more help, you can Refer to our video in Class 8 Maths in Lesson no 27 Euler’s Formula. Check out the video Lesson for a better understanding.
Solved Examples
Example1: Can a polyhedron have 11 faces, 22 vertices, and 33 edges?
Solution: This can be verified easily by Euler’s formula.
F + V – E = 2
Given, faces(F) = 11
Vertices (V) = 22
Edges(E) = 33
Now putting these in the above formula,
LHS =F + V – E
=11+22-33= 0
RHS = 2
LHS does not equal RHS.
Hence , There is no polyhedron for the given conditions.
Example 2: Find the number of faces, edges, and vertices for a triangular prism?
Solution: A prism may be a solid that has five faces, six vertices, and nine edges.
Example 3: How many vertices (corners) does a cube have?
Solution: 8.
Example 4: How many faces, edges, and corners does a pentagonal prism have?
Solution: The pentagonal prism has 7 faces, 15 edges and 10 corners.
Example 5: How many faces, edges, and corners does a Triangular Pyramid have?
Solution: A Triangular Pyramid has 6 edges, 4 corners, and 4 faces.
Example 6: Which of the following solids has a curved edge?
Solution: Cone: A cone has just one edge which is curved – it is a circle.
Cube: A cube has 12 straight edges.
Triangular prism: A triangular prism has 9 straight edges.
Triangular pyramid: A triangular pyramid has 6 straight edges.
Example 7: A solid has 14 faces and 12 vertices. How many edges does the solid have?
Solution: Polyhedral Formula/Euler’s Formula = F + V – E = 2
Therefore, 14 + 12 – E = 2.
or,26 – E = 2
or, E = 26 – 2 = 24
or,E = 24
Therefore, the solid has 24 edges.
Example8: How is a cone defined in terms of faces, edges, and vertices?
Solution: 2 faces, 1 edge, and 1 vertex.
One of the faces is the circular base, the other is the continuous curved part.
The one and only edge is the edge of the circular base, where the two faces meet.
The vertex is the point at the top (the sharp corner).
Summary
- The vertices of a geometry can be defined as corners.
- The line segment between the faces is called an edge.
- A flat surface is called a face.
- Vertices, faces, and edges are three properties that define any 3D or 2D body.
- A polyhedron is a three-dimensional solid made up of polygons. It has a flat surface, straight edges and corners.
- Euler’s formula = F + V – E = 2.
Frequently Asked Questions
1. What do you mean by vertices also give one example?
The vertices of a geometry can be defined as corners. For example: Consider a rectangle: It has four vertices (plural of vertex). Because it has four corners and at every corner 2 edges meet.
2. What is faces? Give one example.
A flat surface is called a face. In the others words A face is a single surface of a solid body. For example, a polyhedron has four faces.
3. What do you mean by edges? Give one example.
The line segment between the faces is called an edge. For example, a pentagon has five edges.
4. What is the relation between vertices, edges, and faces?
Euler’s formula specifies the relationships between faces, edges, and vertices.
Euler’s formula can be expressed as:
F + V- E = 2
5. What is solid shape?
A solid is a 3D shape with length, width, and height (depth). Cube, cone, sphere, and rectangular parallelepiped are examples of three-dimensional shapes.

