There are two types of shapes: two-dimensional shapes and shapes in flat-plane geometry. They can have any number of sides, and their sides can be either straight or curved. Polygons are plane geometric shapes comprised of lines. Polygons include shapes like triangles and squares. For instance, we can state that 2-D figures are those paper drawings that simply have length and width.
Define Plane
A plane is a two-dimensional surface that can stretch indefinitely in both directions and is measured by two linearly independent locations. In algebra, the points are plotted on a number line that runs continuously and infinitely from left to right, up and down, and in all directions. Two planes can cross each other, be identical to one another, and be in parallel with one another. A plane consists solely of a surface with no depth or width. There are only ever two dimensions. If you imagine a wall and extend it indefinitely, it will turn into a plane.
Plane Figures and Shapes
Squares, rectangles, triangles, circles, pentagons, octagons, hexagons, ovals, and other shapes are examples of plane figures. Circles and ovals are not polygons, but shapes like squares and rectangles that gather together are known as polygons.
A closed two-dimensional or flat surface figure is referred to as a plane shape, as opposed to a solid shape. Instead of having edges and faces, they have a number of thin lines that meet to form a corner or a vertex. Triangles, squares, rectangles, circles, and ovals are some common plane shapes. If we looked closely at a piece of paper, we would see its length and width but not its depth; therefore, since they are created by combining two straight or curved lines, they are closed objects. They are also referred to as polygons or planned geometric shapes.
Examples of Plane Shapes

Squares, rectangles, triangles, circles, pentagons, octagons, hexagons, ovals, etc. are examples of plane shapes.
Triangle: A triangle is a polygon with three sides and three angles.
Quadrilateral: A closed polygon with four sides is referred to as a quadrilateral. Trapezium, Square, Rectangle , rhombus, etc are the examples of quadrilaterals.
Circle: A figure is referred to as a circle if all of its points are equally spaced from a fixed point. The fixed point is referred to as the circle’s center.
Pentagon: A shape is referred to as a pentagon if it has five sides.
Hexagon: A shape is referred to as a hexagon if it has six sides.
What are Solid Shapes?
What kind of device, a laptop or computer, are you using to read this? Cuboidal! That is correct! Describe a cuboid. It has a strong form. The same applies to cones, cylinders, etc. Solids are shapes that can be observed and measured in three dimensions. Solid shapes are characterized by their length, width, and height, which can also represent thickness or depth. When a two-dimensional object is folded into a three-dimensional shape and put down flat to reveal each face, the result is known as a net pattern. A net is a 3D figure that has been unfolded. Faces, vertices, and edges are the three primary characteristics of solid forms.
Plane Figures and Solid Shapes in your math class? Don’t worry – our online Math tuition can help! We provide comprehensive lessons on these topics, covering everything from basic shapes to more complex geometric figures.
Solid Shapes Examples

Cubes, cuboids, pyramids, prisms, cylinders, spheres, cones, torus, trapezoids, rhombus, parallelograms, and quadrilaterals are a few examples of solid shapes. A pen is made up of two cylinders, and a dome is made up of a hemisphere on a cylinder or a cone. It can also be formed up of two or more actual figures.
Cuboids: Cuboids can be found in everyday objects like bricks, tiffin boxes, books, matchboxes, etc.
Sphere :Globes, marble, oranges, and bubbles are all examples of spheres in everyday life.
Cone: Ice cream cones, traffic cones, party caps, and other objects in everyday life are examples of cones.
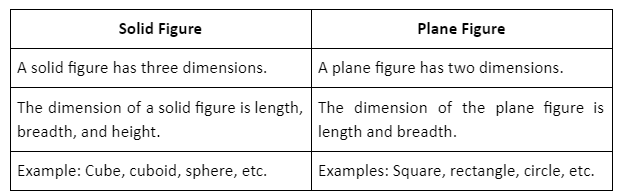
Difference between Solid and Plane Figure
Interesting Facts
- When a specific shape is made repeatedly without any gaps or overlapping and covers a plane, the result is a tessellation. Only squares, equilateral triangles, and rectangular hexagons can form regular tessellations.
- Natural tessellation examples include the hexagonal cells in a honeycomb design or the diamond-shaped pattern on a snakeskin.
Solved Examples
1. A cube with a side length of 6 cm has what size surface area?
Ans: The surface area of a cube is \(6{a^2}\).
The area of the surface area is \(6 \times {\left( 6 \right)^2} = 216c{m^2}\)
2. If the radius of a circle is 7 cm, then what is the area of the circle?
Ans: The area of a circle is \(\pi {r^2}\)
The area of a circle is \(\pi {7^2} = \frac{{22}}{7} \times {7^2} = 154c{m^2}\)
Key Features
- Two linearly independent points can be used to measure a plane, which is a two-dimensional surface.
- Squares, rectangles, triangles, circles, pentagons, octagons, hexagons, ovals, and other shapes are examples of plane figures.
- A plane shape is a closed, two-dimensional or flat surface figure.
Frequently Asked Questions
1. How has geometry and math gotten so much attention because of the ancient Japanese technique of origami?
Ans: Geometry, mathematics, and engineering have all taken a keen interest in origami, the art of folding paper into three dimensions. It offers a fascinating method for converting a flat plane shape into a solid shape. For instance, methods have been devised for the deployment of airbags in a car and stent implantation from a folded state. A crease pattern can also be folded into a 2D representation. Additionally, it is used to double the cube and trisect an angle.
2. What is Euclidean geometry?
Ans: The study of solid and flat shapes using the axioms and theorems developed by the Greek mathematician Euclid is known as Euclidean geometry (c.300 BCE). The solid and plane geometry is known as euclidean geometry. Angles and circles are two instances of Euclidean geometry. The discipline known as parabolic geometry is based on Euclid’s five postulates. There are two types: solid geometry, which is based on Euclidean geometry in three dimensions, and plane geometry, which is based on Euclidean geometry in two dimensions.
3. What is the point?
In a plane, a point is a dot that has no length, breadth, or height. It establishes a plane’s location. There are two different kinds of points: coplanar and non-coplanar points, as well as collinear and non-collinear points. Non-collinear points do not sit on the same line as collinear points, which are located there. Non-coplanar points do not lie on the same plane as coplanar points, which are parallel to one another.

