Introduction
Two lines can intersect at any point or come together at a common point to form an angle. An angle is defined as having two arms that extend outward, and its measurement is expressed in degrees. Angles in pairs are the related angles. Any pair of angles that have a specific relationship between them is therefore referred to as related angles. A specific name refers to these angles. Since the angles are related to a particular circumstance, they are known as related angles.
Related Angles
Related angles are those that have a particular relationship with one another. Each pair of connected angles is given a unique name. There is a specific standard for the associated angles.
Types of Related Angles
The related angles have specific names depending on the type of criteria. When the sum of the two angles is 90 degrees, they are said to be complementary angles. If the sum of the two angles is 180 degrees, they are said to be supplementary angles. In a plane, two angles are said to be adjacent if they share a common vertex, a common arm, and non-common arms that are on the opposite side of the common arm. Due to their shared arm, adjacent angles always lie next to their other pair. The two adjacent angles are regarded as a linear pair of angles when the sum of their respective measures equals 180 degrees. Since their non-common arms are two rays pointing in opposite directions, they are known as linear pairs of angles. When a transverse crosses parallel or non-parallel lines, various angles are created. Alternate exterior angles, alternate interior angles, vertically opposite angles, and corresponding angles are the different types of angles.
Complementary Angles
Complementary angles are those where the sum of the measures of two angles is 90 degrees.

Supplementary Angles
These angles are referred to as supplementary angles when the sum of the measures of two angles is 180 degrees.

Adjacent Angles
If two angles in a plane share a vertex, a common arm, and their non-common arms are located on opposite sides of the common arm, then the angles are said to be adjacent.
Adjacent Angles: Linear Pair
If two adjacent angles share a common vertex, a common arm, and non-common arms that are oriented in opposition to one another, they are referred to as linear pairs of angles.
Alternate Exterior Angles
The angles outside the parallel lines and on the opposing sides of a transversal that intersects parallel lines are referred to as alternate exterior angles. Every other exterior angle is equal.

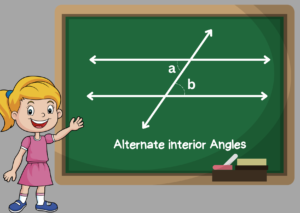
Alternate Interior Angles
The angles inside the parallel lines and on the opposing sides of a transversal that intersect parallel lines are referred to as alternate interior angles. All of the interior angles alternately are equal.
Vertically Opposite Angles
The angles are formed by two lines’ intersections, which are opposite. The angles that are vertically opposite are always equal in size.

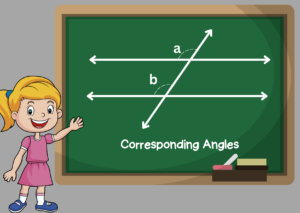
Corresponding Angles
The angels that are lying parallel to the lines and on the same side of the transversal are always equal. Corresponding angles is the name given to these angles.
Interesting Facts about Related Angles
The linear angles’ and supplementary angles’ combined measures are equal. But the specifications for each of these angles vary. The placement of the angles is what causes this. A common arm will always connect the linear pair of angles. The supplementary angles, however, don’t always follow the same pattern. As a result, while all supplementary angles are not linear pairs, all linear pairs are supplementary angles.
Solved Examples
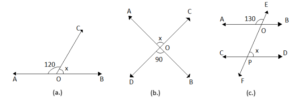
Example: Solve for x in the following images.
Solution:
1.This is a linear pair that lies on line AB.
∠AOC + ∠COB = 180°
120° + x = 180°
x = 180 – 120
x = 60°
1.This is a pair of vertically opposite angles
x = 90°
1.Here, we have no direct connection between a given angle and the angle measured x.
Thus, we will use corresponding angles to find ∠CPO, to use the relation between ∠CPO and x.
∠CPO = ∠AOE
∠CPO = 130°
Now, ∠CPO and ∠OPD are a linear pair on the line CD.
∠CPO + ∠OPD = 180°
130 + x = 180
x = 180 – 130
x = 50°
Summary
There are specific requirements for the related angles. There are always two of them. The angles are referred to as supplementary angles if the total of the pair of angles is 180 degrees. The complementary angle pairs also add up to 90 degrees. The angles that are next to each other are those that have a common arm and other arms that are on different sides of the common arm. Adjacent angles make up the linear pair of angles. The linear pair of angles add up to 180 degrees.
Frequently Asked Questions (FAQs)
1.What are Related Angles?
Ans. Related angles are a pair of angles that have some sort of relation in their geometric structure, which gives them a relationship mathematically using a simple equation.
2.What is the Relationship between Angles on the Same Side of Transversal?
Ans. Angles on the same side of the transversal are shown below,
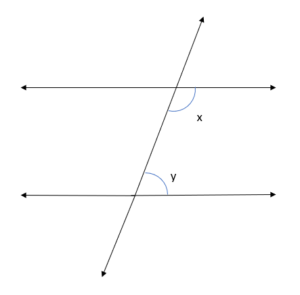
These angles are supplementary to each other, i.e., the sum of these two angles is 180 degrees.
In a pair of lines and a transversal, if corresponding angles are equal. What does it say about the pair of lines?
If in a pair of lines and a transversal, if the corresponding angles are equal, the pair of lines are parallel.
3.Are all Supplementary Angles Linear Pairs?
Ans. No, all supplementary angles are not linear pairs, since by definition linear pairs are the adjacent angles whose sum is 180 degrees, but for supplementary angles, the condition of adjacent angles need not be fulfilled.