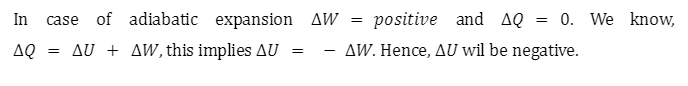Tag: Thermodynamics

Introduction

In thermodynamics, we explore various variables, including temperature, pressure, volume, entropy, heat, etc. These variables form the foundation for thermodynamic processes, which may be classified into isothermal, isobaric, adiabatic processes, etc. 

In an adiabatic process, thermodynamic variables can change value so long as no exchange of heat occurs. There are two critical requirements for such a process to occur:

1. The walls of the piston must be sealed to prevent heat exchange between the system and the environment. 
2. The process of compression or expansion must be completed rapidly.

 

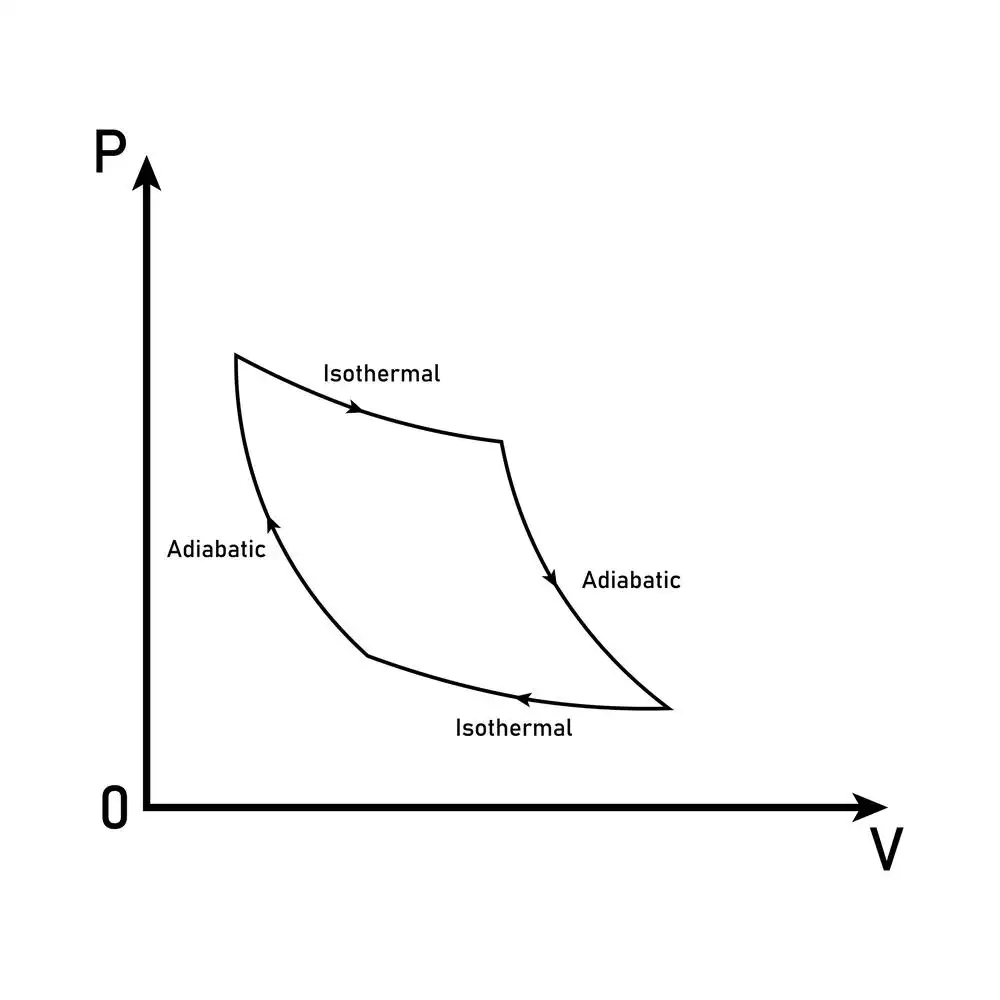
Adiabatic processes

Derivation of adiabatic process formula

Adiabatic Relations between P, V, and T

The first law of thermodynamics gives rise to the conservation of energy, forbidding it from being created or destroyed.

 

Adiabatic relation between P and V

As per the first law, the change in heat energy is equal to the sum of the change in internal energy and the work done. That is,

Adiabatic relation between P and T

We again start with a mole of an ideal gas. Then, from the ideal gas equation,

 Adiabatic relation between V and T:

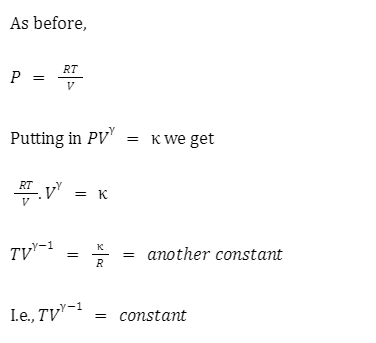
Examples of Adiabatic Process

1. An ice-box prevents heat from entering the system and thus, is an adiabatic system.
2. Hot water kept in a thermal flask is an example of an adiabatic system.
3. When warm air rises from the Earth’s surface, it expands adiabatically. As a result, the water vapour cools and condenses into water droplets forming a cloud.
4. A gas being compressed or undergoing rapid expansion is an adiabatic process since there isn’t enough time for heat exchange to occur.

Adiabatic Expansion

Adiabatic expansion is defined as a perfect condition for a confined system, where the pressure remains constant, and the temperature decreases.

Work done in an adiabatic expansion process

To derive the formula for work done, we start with a closed cylinder that contains n moles of an ideal gas. If P represents the pressure of this gas, and the piston in the cylinder moves up by a distance x, the work done by the gas may be written as:

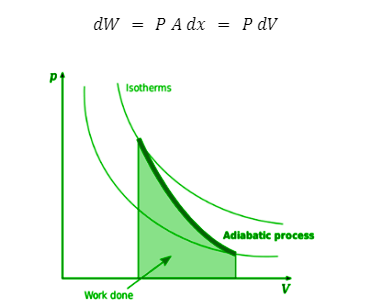
Adiabatic work done

Description: The work done in an adiabatic process is the area under the curve

Here, A represents the cross-sectional area of the piston and dV = Adx is the increase in volume due to the piston’s movement. Suppose the initial and final stages of the system are \(\;({{\bf{P}}_1},{{\bf{V}}_1},{{\bf{T}}_1}){\bf{and}}({{\bf{P}}_2},{{\bf{V}}_2},{{\bf{T}}_3})\), respectively. Then the total work done is:

Shown above is the equation for the work done in an adiabatic process for a system consisting of n moles of an ideal gas. When the gas does work during adiabatic expansion, the work done is positive and the temperature of the gas decreases\(\left( {{T_2} < {T_1}} \right)\). Conversely, when work is done on the gas during adiabatic compression, the work done is negative and the temperature of the gas increases \(\left( {{T_2} > {T_1}} \right)\)

.

Adiabatic Compression

Adiabatic compression is a process wherein, a system undergoes compression without exchange of heat with its surroundings. It leads to an increase in temperature and a decrease in volume.

Adiabatic-reversible and irreversible process

Reversible adiabatic process: An adiabatic process is said to be reversible if the system can revert back to its original state after the process has taken place. Such a process isn’t possible in nature.

Irreversible process: An irreversible adiabatic process is one that cannot be reversed. It is accompanied by an increase in entropy and all real adiabatic processes are irreversible.

Conclusion

An adiabatic process is characterized by changes in the pressure, volume, and temperature of a system, but with no exchange of heat taking place between the system and its surroundings. For an adiabatic process to occur, certain conditions must be met: the walls of the container must be insulated, and the speed of compression or expansion must be rapid enough to prevent heat exchange.

For an adiabatic process, the relation between pressure and volume is \(P{V^\gamma } = \kappa \). This equation may be rewritten in terms of pressure and temperature as\({P^{1 – \gamma }}{T^\gamma } = {\rm{constant}}\), or in terms of volume and temperature as \({\rm{T}}{{\rm{V}}^{\gamma  – 1}} = {\rm{constant}}\)

The work done for an adiabatic process is given by the following expression:

Wadia = nR-1 T1 – T2

 

Frequently Asked Questions

1. The adiabatic process occurs at rapid rate. Explain why?

If the process were to occur slowly, it would give the system time to exchange heat, which would make the process non-adiabatic.

2. During the Adiabatic expansion, the temperature of gas gets lowered. why?

During adiabatic expansion, work is done by the system, causing a decrease in its internal energy. This lowers its temperature.

3.Difference between the Adiabatic and Isothermal processes?

4. Is the work done in an Adiabatic process change depending on which physical quantity?

5.  In adiabatic expansion, how the internal energy is affected? 

 

 

 

Introduction

The whole universe is composed of two parts; system and surroundings. There occurs an exchange of heat between the system and the surroundings. Thermodynamics tells us about the exchange of heat, different forms of energy, and the transformation of energy into work. It also explains some other properties of the system like temperature, pressure, density, enthalpy, entropy, etc.

Define Thermodynamics

Thermodynamics is a topic that derives the relationship between heat, energy, work, and temperature. According to thermodynamics, if the system does the work then its value will be negative and when work is done on the system its value will be positive.

Difference between Thermodynamics and Statistical Mechanics

Define System and Surroundings

System: The part of the universe in which all the matter remains is known as a system. 

Surroundings: The other part of the universe outside the system is known as the surroundings. The system and surroundings are divided by a boundary.

Classification of the system:

1. Open system: It has the capacity to exchange both energy and matter with the surroundings. In an open system, both the temperature T and pressure P are constant. For example, the human body.
2. Closed system: This system only exchanges energy with the surroundings. The entropy of a closed system is always constant. For example, water boils using a closed lid.
3. Isolated system: It exchanges neither matter nor energy with the surroundings. For example, a thermos flask is an example of an isolated system. 

Different types of processes in thermodynamics

• Isothermal process: In this process, the temperature (T) of the system is always constant.

1. Isochoric process: Here, the volume (V) of the system is always constant.
2. Isobaric process: In this process, the pressure (P) of the system remains constant.
3. Adiabatic process: In this process, the change in heat (Q) with the surroundings is zero.

Properties of thermodynamics

1. Intensive properties: These properties don’t change with the change in the amount of matter. For example boiling point, melting point, density, etc.
2. Extensive properties: These properties highly depend on the amount of matter in the system. For example mass, volume, etc.

Functions in thermodynamics

1. State functions: These functions change with the change in the state of a system. For example Enthalpy (H), internal energy (U), entropy(S), and density (d). 
2. Path functions: Heat (Q) and work (W) don’t depend on the state of a system, but rather depend on the path of a system. They are called path functions.

Define Enthalpy and Entropy

Enthalpy (H): It is a property of thermodynamics that indicates the overall heat capacity of a system. It is expressed by the sum of the system’s internal energy and the product of the pressure and volume of the system. 

H = U + PV

Depending on the symbol before the value of enthalpy, any reaction can be classified into two parts.

• Exothermic reaction: The reaction is called exothermic when heat is generated during a reaction. The value of enthalpy in an exothermic reaction is always negative.
• Endothermic reaction: When the system absorbs energy from the surroundings to execute a reaction is called an endothermic reaction.  The value of enthalpy in an exothermic reaction is always positive.

Entropy (S): It measures the extent of disorderness of a system. For a spontaneous reaction, entropy S is always negative and for a non-spontaneous reaction, entropy S is always positive.

Thermodynamic potential

Thermodynamic potentials are used to define a particular state of the system. They are internal energy (U), enthalpy (H), Gibbs free energy (G), and Helmholtz free energy (F).

Laws of thermodynamics

• Zeroth law: This law states: “if two bodies A and B are each in thermal equilibrium with some third body C, then they are also in equilibrium with each other.”
• First law: This law states:  “Energy can neither be destroyed nor be created, it can only be transferred from one form to another”. It is also called the “Law of conservation of energy.”

ΔQ = ΔU + W

ΔQ= Change in heat of a system.

ΔU = Change in internal energy of a system.

W = Work done

• Second law: This law states: “any spontaneously occurring process will always lead to an escalation in the entropy (S) of the universe.”

\[\Delta {S_{Total}} = {\rm{ }}\Delta {S_{system}} + {\rm{ }}\Delta {S_{surroundings}} > {\rm{ }}0\]

• Third law: This law states: “the entropy of a system approaches a constant value as the temperature approaches absolute zero.”

\[{S_{T = 0}} = 0\]

Daily life examples of thermodynamics

1. Human bodies sweat, producing heat from the body.
2. Melting of ice cubes.
3. Like A thermodynamic system, the human body exchanges mass and energy with the surroundings.

Summary

A type of heat energy that connects with other types of energy is called thermodynamics. Heat or work are two ways that energy is changed or exchanged. In thermodynamics, there are four processes. They are isothermal, adiabatic, isobaric, and isochoric. Thermodynamics explains many important properties of the system. Energy is the dominant focus of thermodynamics which is how it is used and transforms from one state to another. Thermodynamics frequently includes using heat to generate work like in the engines of automobiles and generating work to transfer heat like in the refrigerator.

Frequently Asked Questions 

1. Why does thermodynamics emphasize energy?

Ans: The first law of thermodynamics defines that the total energy of the system is always conserved. Neither energy can be created nor destroyed. It is only capable to change from one type to another. Like, in the combustion of fuel the chemical energy is transformed into thermal energy.

2. Why is it referred to as free energy?

Ans: Because it is readily accessible at all times, Gibb’s free energy is known as free energy. If necessary, the reaction can obtain this energy without exerting any effort.  Enthalpy (H) and also the product of the system’s temperature (T) and entropy(S) are added to determine the change in Gibbs free energy (G).

G = H +TS

3. What are the drawbacks of thermodynamics?

Ans: Thermodynamics can’t explain any properties of the system quantitatively. It doesn’t include the direction of the flow of heat. It can’t tell anything about the spontaneity of any reaction. These are the drawbacks of thermodynamics.