Tag: Theorem

Introduction

Pythagoras, a Greek philosopher who was born around 570 BC, is remembered by the theorem’s name. The theorem has likely been proved the most times of any mathematical theorem using a variety of techniques. The proofs are numerous, some of which go back thousands of years, and include both geometric and algebraic proofs. The Pythagorean theorem is extremely useful when determining the shortest distance between two points or the degree of the mountain slope. In a right-angle triangle the square of the hypotenuse is said to be equal to the sum of the squares of the two legs.

Right Angle Triangle

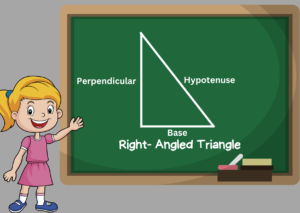
A triangle with a right angle is one in which one angle is 90 degrees. We refer to this triangle as a right-angle triangle since 90 is also referred to as the right angle. Triangle sides with a right angle were given unique names. The side directly opposite the right angle is known as the hypotenuse. Based on the values of the various sides, the right triangles are divided into isosceles and scalene types.

Properties of Right-Angle Triangle

• The height, base, and hypotenuse of a right-angle triangle are its three sides. 
• The two adjacent sides are referred to as base and height or perpendicular.
• Three similar right triangles are formed if we draw a perpendicular line from the vertex of a right angle to the hypotenuse.
• The radius of a circle whose circumference includes all three vertices is equal to one-half the length of the hypotenuse.
• The triangle is known as an isosceles right-angled triangle, where the adjacent sides to the 90° are equal in length if one of the angles is 90° and the other two angles are each equal to 45°.

Pythagoras Theorem

Pythagoras is a potent theorem that establishes the relationship between the sides of a right-angle triangle. According to Pythagoras’ theorem –

“Square of the hypotenuse is equal to the sum of the square of the other two legs of the right angle triangle”. Mathematically, it may be expressed as

              Hypotenuse² = Perpendicular² + Base² 

Area of the Right-Angle Triangle

The area of the right-angle triangle is the region enclosed within the triangle’s perimeter. The formula for a right-angle triangle’s area is.

Area of right-angle triangle = (Base × Perpendicular)

Facts

• A triangle must be a right triangle if it obeys Pythagoras’ theorem.
• The longest side of a triangle is the one that makes the largest angle.
• When the midpoint of the hypotenuse of a right-angled triangle is joined to the vertex of the right angle, the resulting line segment is half of the hypotenuse. In other words, the center of the hypotenuse is the circumcenter of the right-angled triangle.
• If two sides of a right angle are known, we can find the other side using Pythagoras’ Theorem.
• From the provided value of sides, we may determine whether a right-angle triangle is possible.

Summary

A right-angled triangle is one in which one of the angles is a right angle (90 degrees), and the hypotenuse is the side opposite to the right angle. The hypotenuse square of a right-angled triangle is equal to the sum of the squares of the other two sides, according to Pythagoras’ Theorem.

Solved Examples

Example 1: In the right-angle triangle, If PQ = 5 cm and QR = 12 cm, then what is the value of PR?

Solution:  By Pythagoras theorem, we have, 

   Hypotenuse² = Perpendicular² + Base²

PR² = 5² + 12²

PR² = 25 + 144

PR =  = 13 cm

Hence, the value of PR is 13 cm.

Example 2: If a triangle has three sides 9cm, 5 cm, and 7 am respectively, check whether the triangle is a right triangle or not.

Solution: According to the theorem, if the square of the longest side equals the sum of the squares of the other two sides, a triangle is said to be, a right triangle. 

9² = 5² + 7² 

81 = 25 + 49

81 ≠ 74

 Thus, 81 is not equal to 74. Hence, the given triangle is not a right-angle triangle.

Frequently Asked Questions

1.Which Side of a Right-Angled Triangle is the Longest?

Ans: The hypotenuse of a right-angled triangle is its longest side.

2.What is a Right-Angled Triangle’s Perimeter?

Ans: The perimeter of a triangle is the sum of all sides.

Perimeter = base + perpendicular + hypotenuse.

3.Can there be two Right Angles in a Triangle? Explain.

Ans: No, there can never be two right angles in a triangle. A triangle has exactly three sides and interior angles that add up to 180 degrees. This means that if a triangle contains two right angles, the third angle must be zero degrees, which means that the third side will overlap the opposite side. Therefore, a triangle with two right angles is not possible.

Introduction

Although factors and multiples are entirely different concepts, they are related. To determine the factors, we divide the given number by another number, whereas multiples of the given number can be obtained by multiplying the given number by any other number. Multiplication is involved in both ideas. To obtain a given number, we multiply two numbers; the two numbers we multiplied are referred to as the obtained number’s factors.

For example, 4 x 5 = 20. Therefore, 20 is a multiple of 4 and 5, and 4 and 5 are factors of 20.

The number that is the factor of two or more numbers is referred to as the common factor. GCD (Greatest Common Divisor) and HCF (Highest Common Factor) are terms that relate to this idea.

The common multiple is the number that is a multiple of two or more other numbers. The Least Common Multiple, or LCM, is related to this idea. Different divisibility criteria can be used to determine whether a given number is divisible by another without actually conducting the division operation.

Factors

A number must divide completely, leaving no remainder, to be the factor of any other number. In other words, we can also say that the divisor is a factor of the dividend if a number (the dividend) is exactly divisible by any other number (the divisor), leaving no remainder.

For Example: Let’s take the number 36, if we check for factors of 36, we have

36 = 1 x 36 = 2 x 18 = 3 x 12 = 4 x 9 = 6 x 6

Properties of Factors

• If a division of a number by another number leaves no remainder, then that second number is said to be the factor of the first number.
• A number can only have a finite number of factors.
• Prime numbers are those that only have themselves and the number 1 as factors.
• Composite numbers are those that have more than two factors.
• Finding a number’s factors involves using division.
• The obtained factors are always less than the initial number.

Multiples

Multiples are numbers created by multiplying the given number by integers. The multiplication table shows the multiples of a given number.

Properties of Multiples

• The results of multiplying an integer by a given number are referred to as the given number’s multiples.
• There are an infinite number of multiples of a number.
• Finding a number’s multiples requires the use of multiplication.
• The multiples of a given number exceed or are equal to that number.
• Every number is a multiple of itself.

Difference between Factors and Multiples

Some differences between factors and multiples are given in the table below:

Factors	Multiples
Factors are exact divisors of a number.	Multiple has the number as its exact divisor.
Factors of a number are finite.	Multiples of a number are infinite.
Factors are obtained by division.	Multiples are obtained by multiplication.
Factors of a number are always less than or equal to the number itself.	Multiples of a number are always greater than or equal to the number itself.

Common Factors and HCF

A common factor is any factor that two or more numbers share.

For example, take 35 and 42

Factors of 35 = 1, 5, 7, 35

Factors of 42 = 1, 2, 3, 6, 7, 14, 21, 42

Both 35 and 42 have some factors such as 1 and 7 that are common to both, these are known as common factors of 35 and 42.

Now, in this case in the list of common factors, 7 is the largest number, or we can also call it the highest common factor, i.e., HCF.

Thus, HCF or the highest common factor of a set of numbers is defined as the largest number that divides all the numbers in the given set of numbers.

Common Multiples and LCM.

Common multiples are those multiples that are shared by two or more different numbers.

For example, take 6 and 8

Some multiples of 6 are, 6, 12, 18, 24, 30, 36, 42, 48, 54, 60 etc.

Some multiples of 8 are 8, 16, 24, 32, 40, 48, 56, 64, 72, 80 etc.

Here, both 6 and 8 share some common multiples such as 24, 48 and infinitely many more. These are known as common multiples of 6 and 8.

In this case, in the list of common multiples, 24 is the smallest, or we can also call it the least common multiple, i.e., LCM.

Thus, LCM or least common multiple of a set of numbers is defined as the smallest number that is a multiple of or is divisible by all the numbers in the given set of numbers.

Solved Examples

Question: Find the list of factors of 36.

Solution: We know that 1 and the number itself, i.e., 36, are the two trivial factors, so we will start dividing by the next number.

36 ÷ 2 = 18, Thus, 2 and 18 are two more factors of 36, moving to the next number

36 ÷ 3 = 12, Thus, 3 and 12 are two more factors of 36, moving to the next number

36 ÷ 4 = 9, Thus, 4 and 9 are two more factors of 36, moving to the next number

Clearly, 36 is not divisible by 5 since it doesn’t have 5 or 0 in the unit place, moving to the next number

36 ÷ 6 = 6, Thus, 6 is the final factor of 36.

Factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18, and 36.

Summary

This article provides insight into the topic of Factors and Multiples, while also shining a light on the concept of common factors and common multiples. To completely divide another number without leaving any remainder, a number must be the factor of that other number. The multiples are the results of multiplying the given number by integers. Common multiples are those multiples that are shared by two or more different numbers. A common factor exists for two or more different numbers.

Frequently Asked Questions (FAQs)

1. What are Factors and Multiples?

Ans. Factors of a number are defined as the number that divides the given number completely and evenly without leaving any remainder.

Multiples on the other hand are the numbers obtained by multiplying the given number by different integers.

2. What are Prime Numbers?

Ans. Prime numbers are defined as numbers greater than 1 that have only 2 factors, i.e., 1 and the number itself. Some examples of prime numbers are 2, 3, 5, 7, 11, etc.

3. What is the Fundamental Theorem of Arithmetic?

Ans. The fundamental theorem of arithmetic states that every number can be broken into the product of some prime numbers, also known as its prime factors. This product is unique to a number and cannot ever change no matter how you find it, only the order of the product changes.

4. What is the Relationship between HCF and LCM of two Numbers?

Ans. The relationship between is defined as: The product of HCF and LCM of two numbers is equal to the product of the two numbers.

HCF (a, b) × LCM (a, b) = a × b