Introduction
Various geometric parameters such as surface area, volume, etc. to represent the three-dimensional property of a solid. It also indicates the amount of space required to keep an object. The simple geometrical shape we encounter daily includes sphere, cylinder, cube, cone, prism, etc. However, we come to see various objects that are made from a combination of solids. In this tutorial, we will learn about the formula to determine the volume of some known solids and the procedure to evaluate the volume of a combination of solids with solved examples.
What is Combinations of Solids
The combination of solid is the assembly of two or more solids to form a complex one. We cannot rely on simple geometries to meet our daily requirements. Various works require a complex volume that can only be made from a combination of solids. Therefore, combining two or more solids is necessary to get the desired volume. For example, a circus tent can be made by combining two solids, i.e., a cuboid and a cone (as shown in the figure).
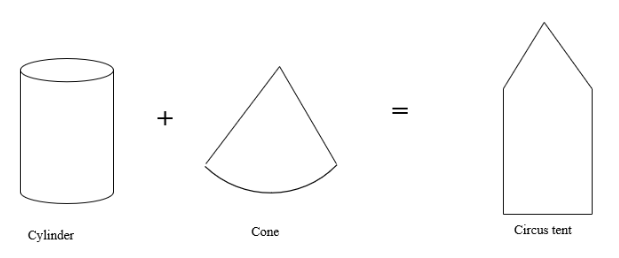
There is a basic mathematical concept behind the combination of solids, i.e., the volume of the combined solid is equal to the summation of the volumes of the individual solids. In mathematically,
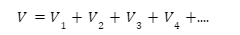
where V= volume of the solid that is formed after the combination

What is the Volume of Some Commonly Known Solids
First, we have to know the volume of some simple geometries to find the volume of the combined solid. Here is a list of the volume of some known geometry.

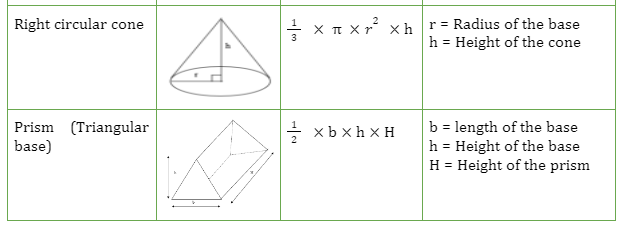
Solved Examples and Word Problems
Example 1:
30 small cylinders are melted and form a larger one. The length and diameter of the small cylinders are 5 cm and 1.4 cm, respectively. Find the length of the large cylinder if the diameter is 2.8 cm.
Solution:

Example 2:
A tent house is made by combining two geometrical structures, i.e., a cylinder and a hemisphere. The height and radius of the cylinder are 20 m and 10 m, respectively. The radius of the hemisphere is 10 m. Find the total volume of the tent house.
Solution:
It is given that,
The radiusr of the cylinder (r) = 10 m
The height of the cylinder (h) = 20 cm
Now, the volume of the cylinder can be obtained by using the formula

Example 3:
A hemispherical part has been removed from a cube in such a way that the diameter of the hemisphere is equal to the side length of the cube. The radius of the hemisphere is 2 cm. Find the remaining volume after removing the hemispherical part.
Solution:

The remaining volume after removing the hemispherical part can be determined by subtracting the volume of the hemisphere from the volume of the cube.
Hence, the volume of the remaining portion is = V=\({V_c-V_h}\)
⇒V=64-16.75=47.25 \({cm^3}\)
∴ The volume of the remaining portion is found to be 47.25\({cm^3}\)
Summary
The present tutorial gives a brief introduction about the volume of a combination of solids. It is based on a basic mathematical concept, i.e., the volume of the combined solid is equal to the summation of the volumes of the individual solids. In addition, the formulae to determine the volume of some known geometries have been depicted in this tutorial. Moreover, some solved examples have been provided for better clarity of this concept. In conclusion, the present tutorial may be useful for understanding the basic concept of the volume of a combination of solids.
Expand your knowledge of mensuration with our 88guru’s online maths tuitions! Join now to learn about other interesting topics. With our 4-day free trial, you can experience the quality of our teaching before committing. Don’t miss out on this opportunity to enhance your mathematical skills!
Frequently Asked Questions
1. Can we determine the volume of an irregular solid?
The volume of an irregular solid cannot be evaluated using the basic formulae that are given in this tutorial. We have to use some other techniques.
2. Will the surface area of the solid geometry equal to the addition of the individual surface area of the solids?
In combination of solids, only volume remains conserved. The surface area of the combined object may or may not equal the addition of individual surface areas of the solids.
3. Give some real-life examples of combinations of solids.
The real-life examples of the combination of solids include ice cream (combination of cone and hemisphere), house (combination of cuboid and hemisphere), etc.
4. If a large spherical ball is cut into two halves, then the sum of the surface area of the two halves will be equal to or larger than the original sphere?
The addition of the surface area of two smaller spheres will be larger than the original sphere. However, the addition of volume will remain unchanged.
5. What is the meaning of volume?
The volume is a geometrical parameter that refers to the capacity of holding by an object. It is also defined as the space occupied by a solid object.