Introduction to the concept of Symmetry
The word “symmetry” is frequently utilized in daily life; instances include the symmetry of butterfly wings, architectural designs, and more. Do you recognize symmetry? When a figure can be folded into two identical halves, we say that it is symmetrical, and as a result, this phenomenon is referred to as symmetry. The line that divides a figure into two identical sections is known as the line of symmetry. In this essay, the two primary symmetries—rotational symmetry and line symmetry—will be adequately explained.
Definition of Line Symmetry and Rotational Symmetry
Line Symmetry
Line symmetry is a type of symmetry that involves reflections. When an object has at least one line that splits a figure in half, with one half being the mirror image of the other, this is referred to as line symmetry, also known as reflection symmetry. The symmetry line might be vertical, diagonal, horizontal, slanted, etc. An imaginary axis or line that splits a figure into two identical halves is called a line of symmetry.
Rotational Symmetry
A fixed point is the centre of many objects. A windmill, a car’s wheels, a clock’s hands, a fan’s blades, etc. are a few examples. When anything rotates, its size and shape stay the same. Rotational symmetry is the ability of a shape to retain its appearance after a revolution. Rotations can occur both in a clockwise and anticlockwise direction. A form or item that keeps its appearance after a given amount of rotation by partial turn has been applied has rotational symmetry.
Therefore, a figure is considered to have rotational symmetry if it fits onto itself more than once throughout a full rotation. A square is being spun here. No matter how it is rotated, the square appears unchanged. As a result, the square acquires rotational symmetry.
Line of Symmetry
An imaginary axis or line that can be used to divide a figure into its symmetrical halves is referred to as a “line of symmetry” in mathematics. It is often referred to as the axis of symmetry. The line symmetry is also called a mirror line because it exhibits two coinciding reflections of the same image. Consequently, it also has a form of reflection symmetry. In most cases, it splits an object in half.
Order of Rotational Symmetry
The number of distinct orientations in which a form maintains its inherent shape is related to the order of rotational symmetry of that shape. A complete turn or full turn is a rotation of \(360\) degrees. In a full turn, there are primarily 4 rotational positions.
rotation of \(90\) degrees.
rotation of \(180\) degrees.
rotation of \(270\) degrees.
rotation of \(360\) degrees.
Shapes of Line Symmetry and Rotational Symmetry
Now we know that some shapes have line symmetry and some have rotational symmetry. Some shapes, respectively, have rotational and line symmetry. We’ll discuss some items’ symmetry right now, which demonstrates both kind of symmetry.
Square: A square \(ABCD\) will always fit exactly onto itself when rotated through \(90\),\(180\),\(270\), and \(360\) degrees about the point \(O\). It has rotational order symmetries as a result. The diagonals and the lines connecting the middles of the opposing sides make up the square’s additional four symmetry lines.
Rectangle: A rectangle \(ABCD\) will always fit exactly onto itself if it is rotated between \(180\)and \(360\) degrees. It has \(2\) rotational order symmetries as a result. Additionally, it has two lines of symmetry.
Equilateral Triangle: An equilateral triangle ABC always fits exactly onto itself when rotated through \(120\),\(240\), and \(360\) degrees about the centroid \(O\). Therefore, the rotational symmetry is of order \(O\). The triangle additionally has three lines of symmetry along the bisectors of the internal angles.
Interesting facts
- Every single regular polygon is symmetrical in shape. If a figure’s rotational symmetry is \(180\) degrees, it has point symmetry.
- The number of sides equals the number of symmetry lines.
Solved Example
Find out the shapes from below, which do not have rotational symmetry
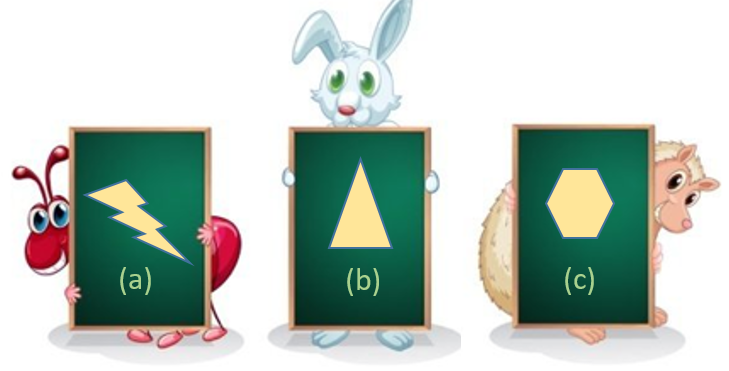
Solution:
- As everyone is aware, rotational symmetry is a type of symmetry where, after rotating a shape in a certain direction, the new shape is the same as the original.
- The preceding figure demonstrates that (b) and (a) lack rotational symmetry as a result.
- There are more symmetric forms, such as the point, translational, gliding, reflectional, helical, etc., but they fall outside the scope of what is now known.
Conclusion
This article provided comprehensive information on line symmetry and rotational symmetry. The rotational symmetry order was also revealed to us. In addition, we discovered the shapes with rotational and line symmetry.
Frequently Asked Questions
1. What do line symmetry and rotational symmetry mean?
If a figure is the same on both sides of a line, it is said to be symmetrical. When a figure can be rotated while keeping its original appearance, it exhibits rotational symmetry.
2. What sets lines of symmetry apart from other lines of symmetry?
The line that divides a figure into two identical sections is known as the line of symmetry. If the shape of an object stays the same when a line is drawn through the middle of it, it possesses line symmetry.
3. In mathematics, what is rotational symmetry?
A form is said to have rotational symmetry if it keeps its appearance after a revolution. Rotations can happen both clockwise and anticlockwise. An object or form’s size and shape don’t change while it rotates. Instead, it revolves around a predetermined location known as the rotating center. This phenomenon is referred to as rotational symmetry.
4. Do right triangles have symmetry along their lines?
A right-angled triangle has non-symmetrical lines. A symmetry line is absent. There is only rotational symmetry of order. The right triangle is isosceles if it only contains one line of symmetry.