Tag: Reflection

Introduction

In simple words, a reflecting surface is a mirror. The research about mirrors dates back centuries, in Germany, mirrors were first created 200 years ago. Famous chemist Justus Von Liebig discovered mirrors in the year 1835, where the transparent glass was converted into mirrors by applying a coating of silver on one side of it. There are several proofs of using polished metal surfaces as mirrors in ancient civilizations. There are some types of mirrors that can reflect sound, which is an intriguing feature of mirrors, known as acoustic mirrors. In World War 2, those that could hear the sounds made by enemy aircraft were used.

What is Mirror?

A reflecting surface is a mirror. The law of reflection governs how a mirror functions. According to the law of reflection, when a light ray strikes a reflective surface, the incident light ray, the reflected light ray, and the normal all lie in the same plane, and the angle of incidence and angle of reflection are both equal.

Improve your Science concepts. Study Science Subject for classes 6th, 7th, and 8th.

Types of Mirrors

There are three types of mirrors that are widely used

a. Plane Mirrors

A smooth reflecting flat surface characterises plane mirrors. We utilise these common mirrors most frequently in our daily life. The reflection of the image in a plane mirror is in the same proportion as the original, but the images are inverted from left to right.

b. Convex Mirrors

Convex mirrors are spherical mirrors. These mirrors have an outward curvature. Convex mirrors provide a simulated, erect, and reduced image. These also go by the name of diverging mirrors.

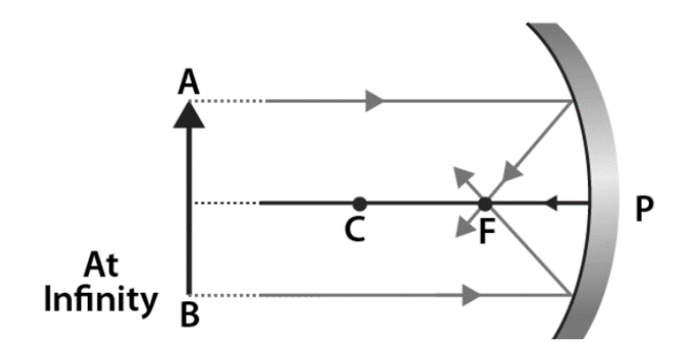
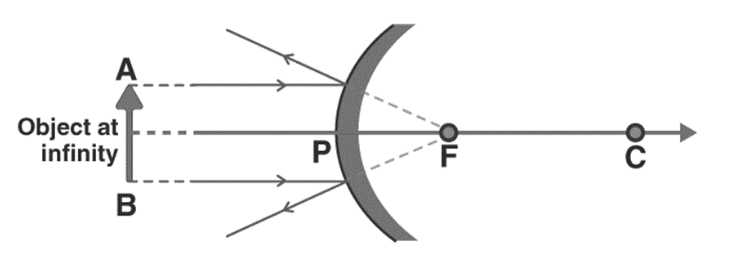
c. Concave Mirrors

Concave mirrors are spherical mirrors as well, but they have an inward curve. The positioning of the object affects the concave mirror’s ability to produce an image. These also go by the name of converging mirrors.

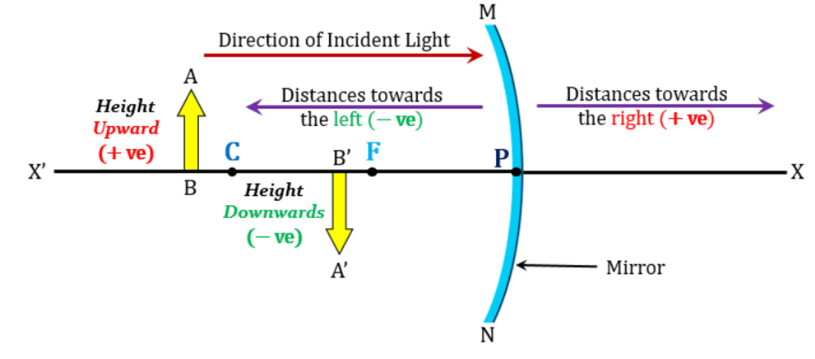
Mirror Formula

The relationship between an object’s distance, an image’s distance, and the focal length of the mirror is given by the mirror equation/mirror formula. If the distance between the object and the mirror is u, the distance between the image and mirror is v, and f is the focal length of the mirror. Then the mirror formula can be expressed as

                                                                                                                      1⁄f = 1⁄u + 1⁄v

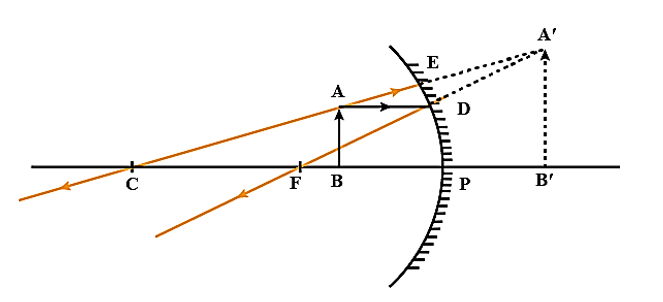
What is Magnification?

Magnification is an increase in the size of the image that a spherical mirror produces about the size of the item. The height of the picture to the height of the object is known as the magnification ratio.

Magnification Formula for the Mirror?

The magnification formula of the mirror can be given as,

                                                                                                m = h‘⁄ h

Where m is the magnification, h’ is the height of the image, and h is the height of the object.

The Magnification Formula of the Mirror can also be given as,

                                                                                           m = –v ⁄ u

where m is the magnification, v is the distance between the image and mirror, and u is the distance between the object and mirror.

Therefore, if the height of the object and image are equivalent, then the magnification will be equal to 1. Magnification will be greater than 1, or the image will be enlarged, if the image size is larger than the object size. Image size will be reduced if the image is smaller than the object, or if the magnification is less than 1.

Concave mirrors can either generate an erect or inverted picture depending on the object’s location, while convex mirrors always provide an upright image. As a result, depending on where the item is maintained, the magnification of a convex mirror is always positive, whereas the magnification of a concave mirror can be either positive or negative. Convex mirrors usually create pictures with lower quality, therefore their magnification is less than 1.

Summary

Concave, convex, or plane surfaces can all reflect light, including mirrors. The relationship between an object’s distance, an image’s distance, and the focal length of the mirror are known as the “mirror equation” or “mirror formula.” Magnification is an increase in the size of the image that a spherical mirror produces about the size of the item.

Frequently Asked Questions (FAQs)

1.What is the Focal Length of a Mirror?

Ans: Focal length is the distance between the Centre of the mirror and the focus of the mirror. And Focus is the point through which the reflected light rays pass when incident light rays are parallel to the principal axis. The focus is on the midpoint of the pole and centre of curvature. We can find the focal length of any mirror using the below formula

                                                                                                           1⁄f = 1⁄u + 1⁄v

In most cases, the focal length is given in millimeters/centimeters. We may determine the angle of view, how much of the scene will be reflected in the mirror, and the mirror’s magnification by looking at the focal length.

2. What is Normal?

Ans: Normal is a line that is drawn perpendicular to the mirror’s surface. The term “Normal line” refers to this line. The incident angle and reflected angle are split into two equal angles by the normal line. It is a fictitious line. The angle of incidence and angle of reflection are terms used to describe the angle between an incident ray and the normal and the angle between a reflected ray and the normal, respectively. To understand what occurs when the angle of incidence, angle of reflection, and angle of refraction vary, a normal is drawn.

3. What is the relation between Focal Length and Magnification?

Ans: Magnification decreases as focal length increases, and thus the mirror magnification is inversely related to the focal length of the mirror. 

Since, the mirror formula can be expressed as,

                                                                     1⁄f = 1⁄u + 1⁄v

And the formula for the magnification of the mirror is,

                                                                   m = –v ⁄ u

Thus, by combining the above two equations, we can get,

                                                                     m = –f ⁄ f-u

Therefore, mirror magnification decreases with increasing focal length, while mirror magnification increases with decreasing focal length. The relationship between the mirror’s magnification and focal length is shown above.

Introduction

To measure the focal length, the distance of the object or image from the mirror, and the mirror’s magnification when studying the reflection of light by spherical mirrors and the generation of pictures by spherical mirrors, several sign conventions must be learned. A spherical mirror‘s pole, sometimes referred to as the origin or origin point, serves as the source of all signals. This sign convention is known as the New Cartesian Sign Convention.

Sign Convention for Reflection by Spherical Mirrors

The sign convention for the mirror was developed with the notion that items are always placed on the left side of the mirror, causing incident light to pass from left to right. For spherical mirrors, the following sign convention applies:

• From the pole, every measurement is taken.
• When measured in the direction of the incoming light, distances are thought of as positive; but, when measured in the opposite direction, they are thought of as negative.
• Upward values are positive and descending values are negative when measuring distances perpendicular to the main axis.

Sign Convention Diagram

Sign Convention for Concave and Convex Mirror

Concave Mirror Sign Convention

• The distance of the object seems to be negative since it is always in front of the mirror.
• The concave mirror’s focal length and radius of curvature are both viewed as negative since the focus and centre of curvature are in front of the concave mirror.
• The distance is determined as – (negative) when the image forms in front of the mirror and as + (positive) when it does so behind the mirror (positive).
• When an image is upright, height is positive; when it is inverted, height is perceived negatively.

Convex Mirror Sign Convention

• The object distance is displayed as negative since the object is always in front of the mirror.
• The radius of curvature and focal length are viewed as + (positive) in the case of a convex mirror since the centre of curvature and focus is located behind the convex mirror.
• Since convex mirrors always form an image behind a mirror, the image’s distance is considered to be positive.
• Since an upright image always forms when using a convex mirror, the image’s height is seen as positive.

Mirror Formula

The distance between an object’s main axis point and the mirror’s pole is referred to as the object distance and is presented by u. The image distance is the distance between a spherical mirror‘s pole and the location of an item on its primary axis and marked with v. Therefore, the formula for the focal length (f) in a spherical mirror can be expressed as                                                                                                                                                                                                      1⁄f = 1⁄u + 1⁄v

Summary

To understand the relationship between the object distance, its image distance, and focal length, the Sign convention is a crucial component of this topic. Additionally, due to the Cartesian system we utilise in the unique mirror sign convention, all mirrors have distinct signs for many variables. We put up a relationship between them using the mirror formula to gain a clearer image, and we can utilise this relationship to solve our numerical difficulties.

Frequently Asked Questions (FAQs)

1. Is the Object Distance Positive or Negative in the Concave Mirror?

Ans: A concave or convex mirror’s object distance is always negative because objects are always positioned on the left side of the mirror, and a spherical mirror’s sign convention dictates that distances to the left of the mirror are always negative. When an image forms on a concave mirror, the image distance v will be negative if it does so on the left side and positive if it does so on the right.

2. What is a Virtual Image?

Ans: Anything that is placed in front of a mirror produces an image. The image is a real image if the object’s light rays strike the mirror, reflect off of it, and then coalesce to form the image. If the image must be produced by extrapolating the reflected light beams backwards rather than converging, it is referred to as a virtual image. Any kind of mirror, whether concave, convex, or planar, may create a virtual picture. These pictures are displayed on the lens or the mirror.

3. What is the Sign Convention we use in the Concave Mirror?

Ans: The object’s symbol is interpreted negatively since it is constantly placed in front of the mirror. The focal length and radius of curvature have negative signs because the concave mirror‘s centre of curvature and focus are in front of it. An image’s height is seen positively while it is upright and negatively when it is inverted. When an image forms in front of the mirror, the distance is estimated as – (negative), and when it forms behind the mirror, the distance is calculated as + (positive) (positive).