Introduction
We see many types of shapes in different objects in our daily lives. Geometry is all around us, so much so that we don’t even notice how many named shapes we see or use for our everyday activities. All such geometrical objects have two measuring quantities, which are Area and Perimeter.
The formula for the area and perimeter of a plane figure can be used to calculate the dimensions of two-dimensional shapes. The perimeter is the distance around the edge of the shape, while the area is the space encircled by any closed figure.
This article focuses on the perimeter and its applications in day-to-day life.
Perimeter
The perimeter of any geometric shape is defined as the sum of the length of all the sides of that figure, or in other words, the total length of the boundary around a geometric shape.
The Perimeter of Commonly Known Shapes.
Usually, the perimeter of a shape can be calculated by simply just adding the length of all the sides of the shape. But some geometric shapes have certain properties that make it easier to calculate the perimeter of that shape using a simple formula, such as any Regular polygon, we know regular polygons have all sides equal, so for any n-sided polygon, we can find the perimeter by simply multiplying the side length by n. Some other geometric shapes whose perimeter can be defined using a formula are given in the table below
| S. no. | Shape | Perimeter Formula |
| 1. | Equilateral Triangles (with sides a) | 3a |
| 2. | Isosceles Triangle (with equal sides a and third side b) | 2a+b |
| 3. | Square (with sides a) | 4a |
| 4. | Rhombus (with sides a) | 4a |
| 5. | Rectangle (with length l, and breadth b) | 2(l+b) |
| 6. | Parallelogram (with adjacent sides l and b) | 2(l+b) |
| 7. | Kite (with two adjacent sides, a and b) | 2(a+b) |
| 8. | Regular n-gon (n-sided polygon) with sides a | n a |
| 9. | Circle (with radius r) | 2πr |
| 10. | Semicircle (with radius r) | πr+2r=(π+2)r |
The Perimeter of a Combination of Shapes.
Unlike the Area, the perimeter does not just simply add up when two or more shapes are combined, rather the perimeter of the combined shape is usually smaller than the sum of its parts depending on the type of combination.
For Example, take this pentagon-looking shape formed using combining a square and an equilateral triangle of the same side length by their sides.
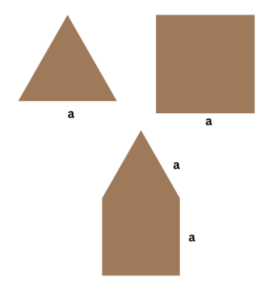
Here, from the previous section, we know that
Perimeter of Triangle = 3a
Perimeter of Square= 4a
The perimeter of the Combined Shape = 5a < 3a + 4a = 7a
Uses of the Perimeter in Real Life
Perimeter does not quite find any major use in real life, except for measuring boundaries of fields or buildings for fencing purposes. A similar kind of use of fencing is during Christmas when we measure the perimeter of rooms in our house to hang Christmas lights along the walls. Perimeter is used to measure the fences around a protected area, it is also used to calculate the cost of putting the fence. As said before, perimeter does not have a variety in its applications. However, the perimeter can be used to calculate the lateral/curved surface area of 3d objects such as Prisms and Cylinders.
Area
The area is defined as the measure of the region enclosed within the boundaries of a shape.
Solved Examples
Example: What is the perimeter of an isosceles trapezium whose parallel sides are 10 m and 12 m, and the non-parallel sides are 5 m?
Solution: The perimeter of a trapezium has no specific formula; thus, we will simply add all the sides to find the perimeter.
Perimeter = Sum of all the sides
Perimeter = 10 + 12 + 5 + 5 = 32m
Example: What is the perimeter of the following shape, which can be described as a small square cut out from a large square? How does the perimeter of the larger square change from this change in its shape?
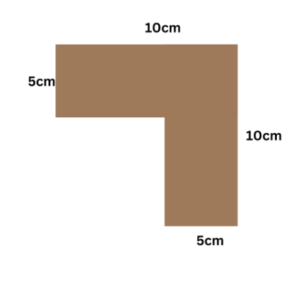
Solution: Here, in this image, we can see that the shape is a square on the side of 10 cm, and from it, a smaller square on a side of 5 cm is cut out.
The length of the sides remaining on the larger square is = 10cm – 5cm = 5cm.
Thus, we can calculate the perimeter now, as all the sides are known.
Perimeter = 10cm + 10cm + 5cm + 5cm + 5cm + 5cm = 40cm.
Also, the perimeter of the original large square is 4a = 4 × 10cm = 40cm.
Thus, there is effectively no change in the perimeter of the large square.
Summary
This article discusses the topic of Perimeter, the Perimeter formula for some commonly known shapes, while also shining a light on the uses of the perimeter in daily life. The perimeter of a geometric shape is defined as the length of the boundary of that shape. Perimeter is used to calculate the fencing around objects or places.
Frequently Asked Questions
1. What do you mean by Perimeter? How will you explain it to someone who has no Mathematical Knowledge?
Ans. Perimeter is defined as the length of the boundary of a geometric shape. To a person who does not know in this regard, we can explain the perimeter as, suppose we take a rope and encircle it tightly along the edges of a shape, then the length of that rope is the perimeter of the shape.
2. What will be the Perimeter of a Square, which has the same area as a Circle with a Radius of r?
Ans. The area is given to be equal, so we will find the length of the side of the square using the areas, and then use that to find the perimeter.
Area of the circle = πr²
Area of a square = a²
Area of the square = Area of the circle
a² = πr²
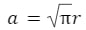
The perimeter of the square = ![]()
3. What is the use of Perimeter in the Calculation of the Lateral Surface Area of any Prism?
Ans. The lateral surface area of a prism is calculated using the formula
LSA = Perimeter of the base × Height
Thus, the perimeter of the base is used to calculate the lateral surface area of a prism.
4. What are the differences between Perimeter and Area?
| Perimeter | Area |
| Perimeter is defined as the measure of the length of the boundary of a geometric shape. | The area is defined as the measure of the 2D region entrapped within the boundaries of a geometric shape. |
| Perimeter is a 1D quantity. | The area is a 2D quantity. |
| Perimeter is measured in the unit of length. Thus, its SI unit is m (metres). | The area is measured in the square of the unit of length. Thus, its SI unit is m2 (square metres) |