Tag: Parallelograms

Introduction

A quadrilateral that can be completely inscribed in a circle is called a cyclic or inscribed quadrilateral and conversely, a circle passing through all four vertices of a quadrilateral is known as a circumcircle. The centre of such a circle is called the circumcentre and the radius is known as the circumradius. Another way of saying that a quadrilateral is cyclic is to say that its vertices are concyclic. Interestingly, while you can inscribe all triangles into a circle, the same is not possible with all quadrilaterals and instead, only some of them can be cyclic.

Definition – What is cyclic quadrilateral

A quadrilateral with all its vertices lying on a circle is called a cyclic quadrilateral. However, not every quadrilateral can be inscribed in a circle and thus, the quadrilateral must be cyclic by design.

The figure below shows a cyclic quadrilateral EFGH inscribed inside a circle. Its sides are represented by e, f, g, and h, and the diagonals are represented by p and q. Note that the diagonals need not be of equal length.

A cyclic quadrilateral

Angles

Angles opposite to each other inside a cyclic quadrilateral sum up to 180⁰, i.e., they are supplementary. For instance, in the figure shown above, we have a cyclic quadrilateral EFGH. If the angles made at the vertices of this quadrilateral are represented by ∠E, ∠F, ∠G, and ∠H, respectively, then we can write the following:

\(\angle E + \angle G = {180^0}\)

\(\angle F + \angle H = {180^0}\)

Further, just like all other quadrilaterals, the sum of all the angles of a quadrilateral is equal to 360⁰ and this can be easily proven by adding the two equations written above.

Radius

There are a few other interesting properties related to the side lengths of a cyclic quadrilateral. Given the cyclic quadrilateral EFGH as above, we can write the following:

semi perimeter of circumcircle, s = \(\frac{{e + f + g + h}}{2}\)

Radius of circumcircle\(r = \frac{1}{4} \times \sqrt {\frac{{(eg + fh) \times (eg + fh) \times (eh + fg)}}{{(s – e) \times (s – f) \times (s – g) \times (s – h)}}} \)

Diagonals

Once again, we look at the cyclic quadrilateral we saw above, with diagonals represented by p and q. Another interesting property that emerges is between the side lengths and diagonals of such a quadrilateral. We can write the following:

length of diagonal p \( = \frac{{(eg + fh) + (eh + fg)}}{{(ef + gh)}}\)

length of diagonal q \( = \frac{{(eg + fh) + (ef + gh)}}{{(eh + fg)}}\)

Area

We can also examine properties related to the area of cyclic quadrilaterals. Looking at the figure shown before, if we have the semi perimeter given by s, we can write the following:

semi perimeter s \( = \frac{{e + f + g + h}}{2}\)

Area \( = \sqrt {(s – e) \times (s – f) \times (s – g) \times (s – h)} \)

Theorems

Ptolemy’s theorem: This is an interesting theorem related to cyclic quadrilaterals. Let us discuss and prove it. As before, we have a cyclic quadrilateral represented by EFGH. Using Ptolemy’s theorem, which states that in cyclic quadrilateral, the product of the diagonals equals the sum of the products of pairs of two opposite sides. That is,

\((EF \times GH) + (EH \times FG) = EG \times FH\)

Or,

\({\bf{eg}} + {\bf{fh}} = {\bf{pq}}\)

This can be proven as follows. We take a cyclic quadrilateral ABCD and suppose that K is the point where its diagonals intersect. This is shown in the figure below.

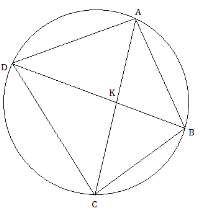
Ptolemy’s theorem

Since the angle subtended by a chord are the same at any point on the circle, we can write for chord AD, chord BC, and chord AB,

∠ABD =∠ACD

∠BCA =∠BDA

∠BAC =∠BDC

Ptolemy’s theorem

Next, we take a point E on the diagonal AC such that ∠EBC = ∠ABD. From the previous three equations, we already have ∠BCA =∠BDA and thus, we have two similar triangles, namely, triangle EBC and triangle ABD. Thus, we can write the following:

\(\begin{array}{l}\frac{{CB}}{{DB}} = \frac{{CE}}{{AD}}\\CB \times AD = CE \times DB\end{array}\)

Let us consider this equation 1 and add ∠KBE on both sides of the equation. We then get

\(\begin{array}{*{20}{c}}{\angle {\bf{EBC}}{\rm{ }} + \angle {\bf{KBE}}{\rm{ }} = \angle {\bf{ABD}}{\rm{ }} + \angle {\bf{KBE}}}\\{\angle {\bf{KBC}}{\rm{ }} = \angle {\bf{ABE}}}\end{array}\)

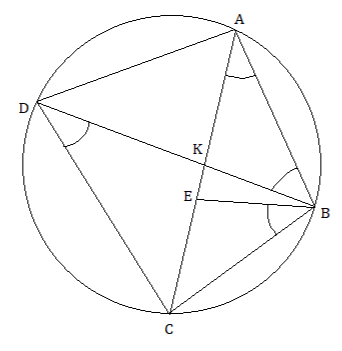
Ptolemy’s theorem

Similarly, we can find similar triangles BDC and ABE and do something similar, leading us to the following relations:

\(\begin{array}{l}\frac{{AB}}{{BD}} = \frac{{AE}}{{DC}}\\DC \times AB = AE \times BD\end{array}\)

We call this equation 2 and add it to equation 1 to get

\(\begin{array}{l}CB \times AD + DC \times AB = CE \times DB + AE \times BD\\CB \times AD + DC \times AB = (CE + AE) \times BD\\CB \times AD + DC \times AB = AC \times BD\end{array}\)

And thus, we have our proof.

Properties

Let’s discuss some properties regarding cyclic quadrilateral:

1. We have discussed that the opposite angles of a cyclic quadrilateral are supplementary. This is always true and thus, if the sum of opposite angles of a quadrilateral is 180⁰, then the quadrilateral is necessarily cyclic.
2. A rhombus can never be a cyclic quadrilateral since its opposite angles do not sum up to 180⁰.
3. Given a cyclic quadrilateral EFGH, with side lengths e, f, g, and h respectively, with diagonals p and q, let the diagonals intersect at a point I. We can write

\(EI \times IG = FI \times IH\)

1. Joining the midpoints of the sides of a quadrilateral gives us a parallelogram.
2. The perpendicular bisectors of the sides of a cyclic quadrilateral meet at the centre and are concurrent.

Problems and Solutions

1. In a cyclic quadrilateral EFGH, \({\bf{if}}{\rm{ }}\angle {\bf{E}}{\rm{ }} = {\rm{ }}{\bf{8}}{{\bf{5}}^{\bf{0}}},{\rm{ }}{\bf{find}}{\rm{ }}\angle {\bf{G}}\)

Since the opposite angles of a cyclic quadrilateral are supplementary, we can write

\(\begin{array}{*{20}{c}}{\angle {\bf{E}}{\rm{ }} + {\rm{ }}\angle {\bf{G}}{\rm{ }} = {\rm{ }}{\bf{18}}{{\bf{0}}^{\bf{0}}}}\\{\angle {\bf{G}}{\rm{ }} = {\rm{ }}{\bf{18}}{{\bf{0}}^{\bf{0}}}–{\rm{ }}{\bf{8}}{{\bf{5}}^{\bf{0}}} = {\rm{ }}{\bf{9}}{{\bf{5}}^{\bf{0}}}}\end{array}\)

2. Let the side lengths e, f, g, and h of a cyclic quadrilateral be 3, 6, 4, and 7m respectively. What is its area?

For a cyclic quadrilateral, the semi perimeter is given by

\(s = \frac{{e + f + g + h}}{2}\)

And the area is given by

\(A = \sqrt {(s – e) \times (s – f) \times (s – g) \times (s – h)} \)

On substituting the values, we get s = 10 m. And therefore, the area is

\(\begin{array}{l}A = \sqrt {(10 – 3)(10 – 6)(10 – 4)(10 – 7)} \\A = \sqrt {7 \times 4 \times 6 \times 3} \\A = \sqrt {504} {m^2}\end{array}\)

3. Let the side lengths of a cyclic quadrilateral be 2, 5, 3, and 6m. Find the product of the diagonals.

We can use Ptolemy’s theorem to solve this problem. We know that

\(\begin{array}{l}EF \times GH + EH \times FG = EG \times FH\\EG \times FH = 2 \times 3 + 5 \times 6 = 36\end{array}\)

Summary

This article discussed what cyclic quadrilaterals are by explaining their definition and listed a few properties related to the sides, angles, the circumcircle, the diagonals, and the area of a cyclic quadrilateral. Further, we looked at a few theorems related to such quadrilaterals, namely, Ptolemy’s theorem.

Enhance your understanding of Cyclic Quadrilaterals by enrolling in our Class 9 Maths Tuitions.

Frequently Asked Questions

1. Is every square a cyclic quadrilateral?

Yes. The sum of the opposite angles inside a square always add up to 180⁰ and therefore, all squares are cyclic in nature.

2. If we are given the lengths of sides of a cyclic quadrilateral, how do we find its diagonals?

Such problems can be solved using the properties of cyclic quadrilaterals. The diagonals p and q of a cyclic quadrilateral EFGH can be obtained via the formulae given below:

length of diagonal p \( = \sqrt {\frac{{(eg + fh) + (eh + fg)}}{{(ef + gh)}}} \)

length of diagonal q \( = \sqrt {\frac{{(eg + fh) + (ef + gh)}}{{(eh + fg)}}} \)

3. Are all parallelograms cyclic quadrilaterals?

Not necessarily. The opposite angles inside a parallelogram aren’t always supplementary and thus, may not add up to 180⁰ , which means that only some parallelograms can be cyclic.

4. How can we prove that the opposite angles of a cyclic quadrilateral are supplementary?

A: We can prove this using the fact that the opposite angles of an inscribed angle are equal. Let ABCD be a cyclic quadrilateral with center O, and let angle ABD be x and angle BCD be y. Then, angle ABC is (180 – x) degrees and angle ADC is (180 – y) degrees, since angles on a straight line add up to 180 degrees. By the inscribed angle theorem, angle ABC is equal to angle AOC, and angle ADC is equal to angle AOD. Therefore, we have:

x + y = angle ABD + angle BCD = angle AOC + angle AOD = angle AOC + (180 – angle AOC) = 180 degrees

Thus, we have shown that the opposite angles of a cyclic quadrilateral are supplementary.

5. What are some examples of real-world applications of cyclic quadrilaterals?

A: Cyclic quadrilaterals are used in a variety of fields, including engineering, architecture, and physics. For example, the design of the circular gears used in many mechanical systems is based on the properties of cyclic quadrilaterals. In architecture, the shape of many domes and arches is based on the geometry of cyclic quadrilaterals.

Introduction

We come across several items of various shapes and sizes in our daily lives. Many items have three sides, whereas others have four, five, and so on. Some forms have equal sides on all sides, whereas others do not. Consider our laptop screen, deck of cards, tabletop, chessboard, carrom board, and kite as examples. What feature does each of these shares? Each of them has four sides.

A quadrilateral is a flat shape with four straight sides. The terms Quadra and Latus combine to make the word quadrilateral. Quadrilaterals are simply shaped with four sides since Quadra means “four” and latus means “sides” in Latin.

One definition of a quadrilateral is a closed four-sided shape. There are many different types of quadrilaterals, including square, rectangle, rhombus, trapezium, kite, etc., supported by the characteristics of sides and angles.

Quadrilaterals

A quadrilateral is a polygon with at least and at most four sides, four angles, and four vertices.

Just like every other polygon, except triangles, the quadrilaterals are also divided into two subcategories,

1. Concave Quadrilaterals: These quadrilaterals have one diagonal passing through outside of the body of the quadrilateral. The following image shows one example of such quadrilateral 
2. Convex Quadrilaterals: These are the normal quadrilaterals, that have all the angles less than \(180^\circ \) , and both the diagonals are always contained within the quadrilaterals.

These are divided into \(2\) more categories

1. Regular: In these quadrilaterals all four sides and all four angles are equal to one another. The only regular quadrilateral is Square.
2. Irregular: In these quadrilaterals, all four sides or all four angles are not equal to one another. There are many irregular quadrilaterals, such as, Rhombus, Rectangle, Trapezium etc.

Properties in Quadrilaterals

Above, we have a quadrilateral \(ABCD\) 

• This quadrilateral has \(4\) sides, and they are \(AB,BC,CD\) and  \(DA\) .
• This quadrilateral has \(4\) vertices, and they are \(A,B,C\) and \(D\) .
• This quadrilateral has \(4\) angles one at each vertex.

Angle Sum Property of a Quadrilaterals

The Angle Sum Property of a Quadrilateral states that the sum of a quadrilateral’s four internal angles is \(360^\circ \) .

I.e., in above example of Quadrilateral ABCD, we have,

\[A + B + C + D = 360^\circ \]

Types of Quadrilaterals

In this section, we will discuss the different types of quadrilaterals and some of their properties.

Square

This is the regular quadrilateral, i.e., all four sides and all four angles are equal to one another. The diagonals are also equal, and bisect each other at right angles. By the property of regular quadrilateral and angle sum property, the angles of the square are right angles.

Rectangles

Rectangles have opposite sides equal and parallel, and all four angles in rectangles are right angles. The diagonals are equal, and they bisect each other but not at right angles.

Also Read: Exterior Angles of a Polygon

Rhombus

Rhombus’ have opposite angles equal, and all four sides in rhombus’s are equal. The diagonals bisect each other at right angles.

Parallelograms

Parallelograms have opposite sides equal and parallel, the opposite angles are also equal in a parallelogram. Diagonals bisect each other.

Trapezium

Trapeziums have only one property, i.e., they have one pair of opposite parallel sides. Other than that they can have any side lengths, any angles, and any diagonals.

Summary

This article taught us about quadrilaterals, including their kinds and qualities. A \(2D{\rm{ – }}shape\) with four sides, four vertices, and four angles is referred to as a quadrilateral. Quadrilaterals come in a variety of shapes, including rectangles, rhombus, squares, trapezoids, parallelograms, and kites. These all feature unique angles and side characteristics.

Frequently Asked Questions

1. Are all parallelograms rectangles? What about the other way around?

Ans. No, all parallelograms are not rectangles. Since to be a rectangle a parallelogram should have diagonals equal, they should also have all the angles to be right angles. Which is not the case for parallelograms. Whereas if we see it other way around, we have the pair of opposite sides parallel and equal to each other and the diagonals also bisect each other, thus all rectangles are parallelograms.

2. What are the properties of a kite?

Ans. Kite is a convex quadrilateral with pair of adjacent sides equal to each other and the diagonals are perpendicular to each other. Also, the diagonal between the equal sides bisects the other.

3. A square has the properties of all three, parallelogram, rectangle and rhombus. Justify this statement.

Ans. A square has following properties.

• Opposite sides parallel and equal. (Parallelogram)
• Opposite angles equal. (Parallelogram)
• Diagonals bisect each other. (Parallelogram)
• Diagonals are equal. (Rectangle)
• All the angles are equal to right angles. (Rectangles)
• All four sides are equal. (Rhombus)
• Diagonals are perpendicular bisectors of each other. (Rhombus)

Thus it is clear that the square has the properties of all, parallelogram, rectangles and rhombus.