Tag: Negative

Introduction

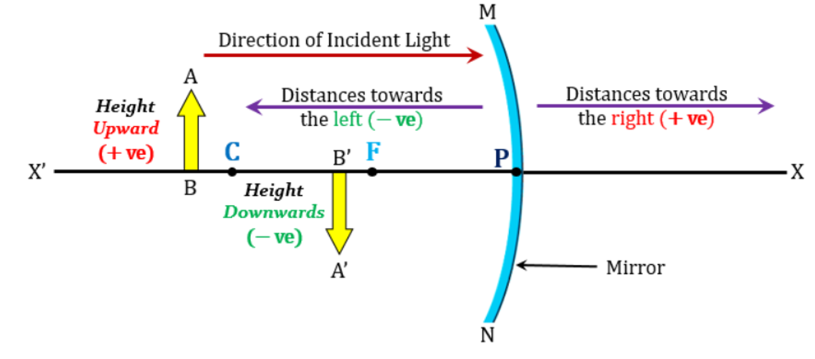
To measure the focal length, the distance of the object or image from the mirror, and the mirror’s magnification when studying the reflection of light by spherical mirrors and the generation of pictures by spherical mirrors, several sign conventions must be learned. A spherical mirror‘s pole, sometimes referred to as the origin or origin point, serves as the source of all signals. This sign convention is known as the New Cartesian Sign Convention.

Sign Convention for Reflection by Spherical Mirrors

The sign convention for the mirror was developed with the notion that items are always placed on the left side of the mirror, causing incident light to pass from left to right. For spherical mirrors, the following sign convention applies:

• From the pole, every measurement is taken.
• When measured in the direction of the incoming light, distances are thought of as positive; but, when measured in the opposite direction, they are thought of as negative.
• Upward values are positive and descending values are negative when measuring distances perpendicular to the main axis.

Sign Convention Diagram

Sign Convention for Concave and Convex Mirror

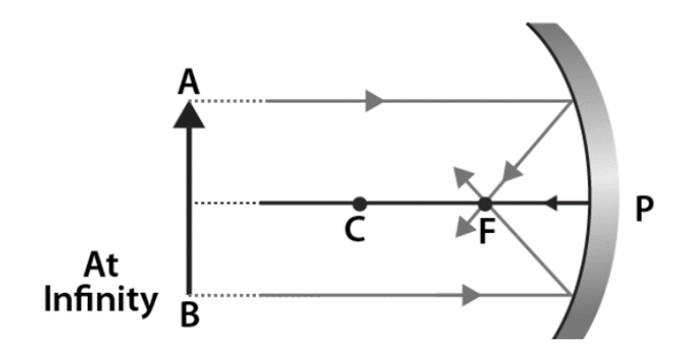
Concave Mirror Sign Convention

• The distance of the object seems to be negative since it is always in front of the mirror.
• The concave mirror’s focal length and radius of curvature are both viewed as negative since the focus and centre of curvature are in front of the concave mirror.
• The distance is determined as – (negative) when the image forms in front of the mirror and as + (positive) when it does so behind the mirror (positive).
• When an image is upright, height is positive; when it is inverted, height is perceived negatively.

Convex Mirror Sign Convention

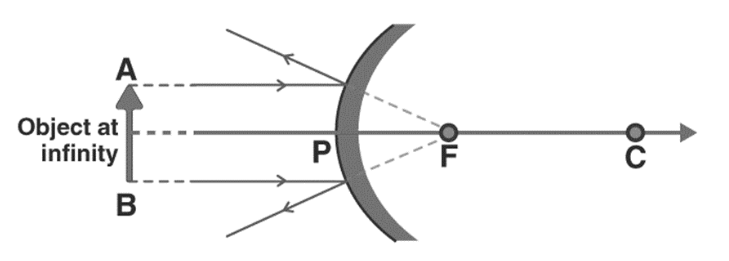
• The object distance is displayed as negative since the object is always in front of the mirror.
• The radius of curvature and focal length are viewed as + (positive) in the case of a convex mirror since the centre of curvature and focus is located behind the convex mirror.
• Since convex mirrors always form an image behind a mirror, the image’s distance is considered to be positive.
• Since an upright image always forms when using a convex mirror, the image’s height is seen as positive.

Mirror Formula

The distance between an object’s main axis point and the mirror’s pole is referred to as the object distance and is presented by u. The image distance is the distance between a spherical mirror‘s pole and the location of an item on its primary axis and marked with v. Therefore, the formula for the focal length (f) in a spherical mirror can be expressed as                                                                                                                                                                                                      1⁄f = 1⁄u + 1⁄v

Summary

To understand the relationship between the object distance, its image distance, and focal length, the Sign convention is a crucial component of this topic. Additionally, due to the Cartesian system we utilise in the unique mirror sign convention, all mirrors have distinct signs for many variables. We put up a relationship between them using the mirror formula to gain a clearer image, and we can utilise this relationship to solve our numerical difficulties.

Frequently Asked Questions (FAQs)

1. Is the Object Distance Positive or Negative in the Concave Mirror?

Ans: A concave or convex mirror’s object distance is always negative because objects are always positioned on the left side of the mirror, and a spherical mirror’s sign convention dictates that distances to the left of the mirror are always negative. When an image forms on a concave mirror, the image distance v will be negative if it does so on the left side and positive if it does so on the right.

2. What is a Virtual Image?

Ans: Anything that is placed in front of a mirror produces an image. The image is a real image if the object’s light rays strike the mirror, reflect off of it, and then coalesce to form the image. If the image must be produced by extrapolating the reflected light beams backwards rather than converging, it is referred to as a virtual image. Any kind of mirror, whether concave, convex, or planar, may create a virtual picture. These pictures are displayed on the lens or the mirror.

3. What is the Sign Convention we use in the Concave Mirror?

Ans: The object’s symbol is interpreted negatively since it is constantly placed in front of the mirror. The focal length and radius of curvature have negative signs because the concave mirror‘s centre of curvature and focus are in front of it. An image’s height is seen positively while it is upright and negatively when it is inverted. When an image forms in front of the mirror, the distance is estimated as – (negative), and when it forms behind the mirror, the distance is calculated as + (positive) (positive).

Introduction

The rate of change in displacement of a moving object is referred to as its velocity. As a result, velocity is a vector quantity, and the velocity-time graph or velocity-time relation is a graphical representation of its fluctuation with time. A velocity-time graph shows the variation of the object’s velocity with time, under different conditions, such as under uniform motion, and under acceleration. On a velocity-time graph, acceleration is depicted by the slope of the graph line.

Velocity-Time Graph for Uniform Motion (No acceleration)

Since there is no acceleration being given to the moving object in this scenario, its velocity is constant and does not fluctuate over time. As a result, in this scenario, it is clear from Figure (a) below that despite the change in time, the velocity will remain constant throughout the entire journey of the object.

Velocity-Time Graph with a Constant Uniform Acceleration

In this situation, the item is subject to a constant uniform acceleration, so depending on the applied uniform acceleration—referred to as the accelerating and retarding acceleration, respectively—its velocity will constantly grow or decrease. We see a linear behaviour of the object’s velocity with time in the velocity-time graph (as shown below in Figure (b)), where the velocity of the item grows linearly on the application of constant uniform acceleration. You can use the slope of this graph to calculate the object’s applied acceleration.

The object’s equations of motion under a uniform constant acceleration can be expressed as follows:

v = u + at

s = ut + 1/2 at²

v² = u² + 2as

Where v, u, a, s, and t are the final velocity, initial velocity, uniform acceleration, total displacement of the object, and travel/trip time, respectively.

Velocity-Time Graph under a Variable Acceleration

As shown in Figure (c) above, in this situation, the acceleration acting on the object varies with time and as a result, the object’s variation in velocity is different during each time period of the journey. As a result, we observe a velocity-time graph that differs from the case where the object is subjected to variable acceleration and observe a parabolic behaviour of velocity with time.

Summary

The rate of change of displacement is known as velocity. The slope of the curves on the velocity-time graphs indicates how quickly the item is accelerating. Any object’s velocity is determined by the rate at which its displacement changes, so its starting and ending positions are crucial.

Frequently Asked Questions

1.What is the Initial and Final Velocity?

Ans: An object’s initial velocity is its speed at time zero, or when it first begins moving, and its final velocity is its speed when the journey has come to an end.

2. State the difference and Similarity between Speed and Velocity.

Ans: The pace at which a distance changes is known as an object’s speed, whereas the rate at which its displacement changes is known as its velocity. Speed and velocity are scalars and vector quantities because distance and displacement are, respectively, scalar and vector quantities. Since both distance and displacement are expressed in meters, there is an m/s correspondence between speed and velocity.

3. What are the differences between Velocity and Acceleration?

Attributes	Velocity	Acceleration
Definition	The speed of an object in a given direction.	Acceleration implies any change in the velocity of the object with respect to time.
Calculated with	Displacement.	Velocity
What is it?	Rate of change of displacement.	Rate of change of velocity.
Formula	Displacement/Time	Velocity/Time
Unit of Measurement	Meter/Second	Meter/second²

4. What do Velocity Time Graphs Show?

Ans: A velocity-time graph displays the sprinter’s object’s changing speed, as well as the speed of any other moving item or person. The slope of the graph line on a velocity-time graph is used to illustrate acceleration. If the line slopes downhill, as it does between 7 and 10 seconds, then acceleration is negative, and velocity is dropping.