Tag: monomial expression

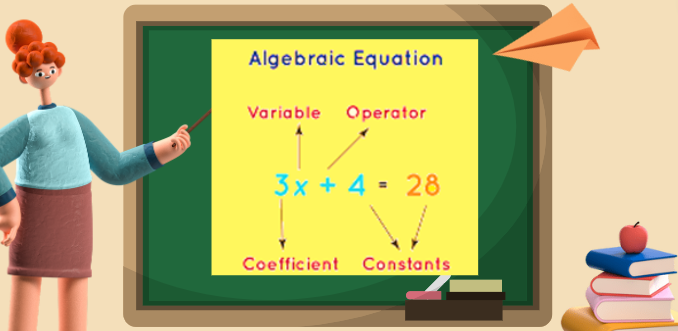
An Introduction

The value of a variable determines the value of an expression. By substituting the variable’s value in the expression and utilizing mathematical procedures, the expression is made simpler. The expression’s value is the outcome that is ultimately obtained. A whole integer, rational number, decimal number, or real number can be the value of the expression. A component of algebra is the expressions. A mathematical expression is made up of a mixture of numbers, variables, and operators. Any number of terms can combine to produce it. Any phrase may have any number of terms, ranging from 1 to n.

Find the value of the expression.

A phrase uses a variety of words. Any expression’s terms are the result of its variables and numbers. As the value of the variable changes, so do the terms’ values. Any number may be the value of the variables. As a result, the expression’s value changes together with the variable’s value. Any number of variables can be used to determine the value of the expressions. The expressions can be rationalized, factored, simplified, or enlarged to get at the answer. An expression’s value can be determined by substituting the values of its variables and then solving the expression. Only the phrasing of the expression determines its value. The value of the expression will always be a positive real number if it is the sum of two positive variables. The expression created by the product of the three negative variables will also always have a value that is a negative real number. Although it is the only possible value for the expression, the value of the variable is always a factor. The values of the variables must therefore be known in order to determine the expression’s value.

Find expression

Any expression is a concatenation of phrases related to mathematical operators +,-, etc. The terms of the expression serve as a clue. Any mathematical expression’s terms must include both numbers and variables. The English alphabets serve as a representation of the variables. Examples of the variables include, x,y,z,a,b,c and others. Defining the terms will help you find the expressions. Below are a few instances of these expressions.

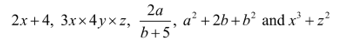
Expression in Mathematics

In algebra, expressions are one of the fundamental ideas. Expressions help you create equations, solve equations, comprehend fundamental principles of functions, and create various forms of equation solutions. Therefore, it is crucial to grasp expressions in mathematics. Expressions may contain a single variable or several variables. Mathematics uses like and unlike terms in its expressions. Finding similar and dissimilar terms in any expression is crucial since doing so simplifies complex statements. By looking at the variables in the following expressions, it is possible to determine the like terms and unlike terms of any mathematical equation. The expressions’ like terms all contain the same variables. On the other hand, there are various variables in the variable portion of the variables. For two words to be similar, their respective variable powers must be equal. Below are a few examples of mathematical expressions.

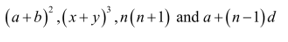
What is an expression in Mathematics?

Mathematical expressions are a collection of terms made up of variables and integers related by the addition, subtraction, multiplication, and division mathematical symbols. After learning how to calculate an expression’s value and identify an expression, explain what an expression in mathematics is. There are many identities in the study of mathematics. Two equivalent formulations make up the identity. For all possible values of the variables, the two sides of the identities are always equal. Following are explanations of a few mathematical expressions.

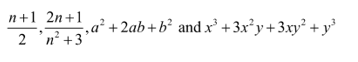
Interesting Facts

• There is never a match between the equations and the expressions.
• Expressions can be made simpler by factoring them, rationalising them, eliminating common terms from the numerator and denominator, and adding and subtracting.
• Only when the values of the variables are equal can two straightforward expressions in the same variable have values that are equal.

Solved Problems

1. Find the value for the expression a+4 when, a=2 and -2.

Sol:

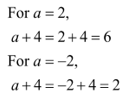
2. Calculate the value for the expression given below for x=1 and 2.

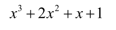
Sol:

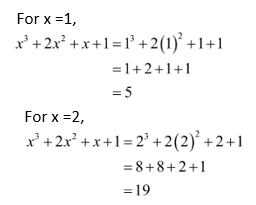
3. Simplify the expression \({y^2} + 3y\) and find its value at y = 0..

Sol: Factorize the given expression.

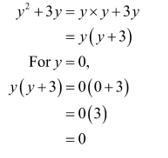
Summary

The expressions are used in mathematics to represent a certain value for different particular values of the respective variables. The variables can be any real values. To find the value of the expression, substitute the values of the variables and then simplify the obtained arithmetic expression. Expression is a combination of the terms with the mathematical operators. To find the expression, identify the terms and check if their combination is an expression or an equation. Expression in Mathematics is used frequently. The expression in mathematics helps to form different numbers of identities.

Practice Questions

Solve the expression x + y for x = 1, y = 2 and x = -2.5 , y = 0

Ans: 

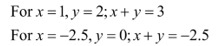
2. Simplify the expression \(\frac{{{x^3} + 2x}}{{3{x^2} + x}}\)and find its value at x =1.

Ans:

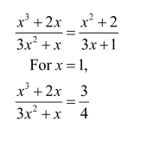
Frequently Asked Questions

1. Are the expressions and equations always the same?

Ans: No. They are not the same.

2. What is the use of expressions in mathematics?

Ans:  Any general rule which is true for different sets of numbers can be represented using the expression.

3.  Can two sets of variables have the same value for the expression?

Ans: Yes. Two sets of variables can have the same value for the expression.

Introduction

Multiplication is one of the basic mathematical operations used in algebraic expressions. We can classify algebraic expressions according to the number of terms they contain, such as monomial, binomial, trinomial, quadrinomial, or polynomial. A monomial expression is a one-term algebraic expression that contains a variable and its coefficients. A monomial multiplied by a monomial: When we multiply a monomial by a monomial, the resulting product will also be a monomial. For example, x, y, 2x, 2y, x2, y2, etc. are all monomials. Monomials cannot have negative exponents.

Now, if we multiply the monomial by the monomial, the result is the monomial. The coefficients of the monomial are multiplied, and then the variables are multiplied. For example, the product of two monomials such as 2x and 2y equals 4xy. If two monomials have the same variable and the same exponent, then we need to use the law of exponentials.

Monomial

Monomials are a type of polynomials with only one term. Monomials algebraic expressions are a type of expression that have only a single term, but can also have multiple variables and higher degrees. For example, \(9{x^3}yz\) is the monomial, where 9 is the coefficient, x, y, z are the variables, and 3 is the degree of the monomial. Similar to polynomials, we can perform different operations on monomials, such as addition, subtraction, multiplication and division.

Monomial example

Let’s consider some variables and  monomial examples:

\(p\) – a variable with a degree of one.

\(5{p^2}\) – The factor is 5 and the degree is 2.

\({p^3}q\) – has two variables (p and q) with degree \(4{\rm{ }}(i.e.,{\rm{ }}3 + 1).\)

\( – 6ty{\rm{ }}–{\rm{ }}t\) and \(y\) are two variables with a coefficient of\( – 6\) .

Let’s consider \({x^3} + 3{x^2} + 4x + 12\) as a polynomial, where \({x^3},{\rm{ }}3{x^2},{\rm{ }}4x\) and 12 are called monomials.

Parts of a Monomial expression

These are the different parts present in a monomial expression are:

• Variable: The letter that appears in the monomial expression.
• Coefficient: The number to multiply by the variable in the expression.
• Degrees: The sum of the exponents present in the expression.
• literal part: the letters that appear with the exponent value in the expression.

Multiplying Monomials

Monomial multiplication is a method of multiplying two or more monomials at a time. Multiplying a monomial by another monomial yields a monomial as the product. Depending on the type of polynomial we use, there are different ways of multiplying.

There are specific multiplication rules for different types of monomials. The constant factor is multiplied by the constant factor, and the variable is multiplied by the variable.

Multiplying a Constant Monomial With a Variable Monomial

Let us consider two monomials \(7\) and \(6y\) . In this case, \(7\) is a constant monomial, and \(6y\)  is a variable monomial. We multiply the coefficients of the constant monomial with the variable monomial. It gives \(7 \times 6 = 42\) . After that, we write the variable \(\left( y \right)\) after \(42\)

Hence, the answer is
\(7 \times 6y = 42y\) .

Multiplying Two Monomials With Different Variables

Consider two monomials with different variables, \(2{x^3}{\rm{ }}\& {\rm{ }}5y\)

First, we’ll multiply by the coefficients. The coefficient of \(2{x^3}\)  is \(2\) , and the coefficient of \(5y\)  is \(5\) . After multiplying, you get \(2 \times 5 = 10\)

Next, we’ll multiply the variables using the exponential rule wherever needed. Here, the variable part is \({x^3}\) &            \(y\) . Multiplying these together, we get \({x^3} \times y = {x^3}y\) because the variables are different. We can multiply them without using the exponential rule.

Hence, the answer is
\(2{x^3} \times 5y = 10{x^3}y\) .

Multiplying Two Monomials With Same Variable

Let us learn the following steps using the example given below.

Considering two monomials \(4{a^2}\;\& \;3{a^4}\).

First, we will multiply the coefficients. The coefficient of \(4{a^2}\)  is \(4\)  and the coefficient of \(3{a^4}\)  is \(3\) . After multiplying, we get \(3 \times 4 = 12\) .

Next, we will multiply the variables using the rule of the exponents. Here, the variable parts are \({a^2}\)  & \({a^4}\) . Multiplying these we get, \({a^2} \times {a^4} = {a^6}\)  as we added the exponents of the variable as per the rule of the exponent.

Hence, the answer is
\(4{a^2} \times 3{a^4} = 12{a^6}\)

Interesting facts

• Multiplying two monomials will also yield a monomial.
• The sum or difference of two monomials may not result in a monomial.
• An expression with a single term with a negative exponent cannot be treated as a monomial. (i.e,) a monomial cannot have variables with negative exponents.

Solved examples

1. Multiply \(x\)  and \({x^2}\) .

Sol: Given two monomials are \(x\)  & \({x^2}\)

First, we’ll multiply by the coefficients. Both monomials have coefficients of \(1\). Therefore, the product is \(1\).

Next, we’ll use the exponential rule to multiply the variables. Here, the variable part is \(x\) & \({x^2}\). Multiplying these together, we get \(x \times {x^2} = {x^3}\)  because we added the exponent of the variable according to the rule of exponent \(3\)  .

Therefore, the answer is \(x \times {x^2} = {x^3}\).

2. Multiply by \(3x\) and \(4y\) .

Sol: Given two monomials are \(3x{\rm{ }}\& {\rm{ }}4y\)

First, we multiply the coefficients. The coefficient of \(3x\) is \(3\), and the coefficient of \(4y\) is 4. After multiplying, you get \(3 \times 4 = 12\)

Next, we will multiply the variables using the exponential rule wherever needed. Here, the variable parts are \(x,y\) . Multiplying these together, we get \(x \times y = xy\) . Since the variables are different, we can multiply them without using the exponential rule.

Therefore, the answer is \(3x \times 4y = 12xy\) .

3. Multiply by \(7{z^3}\) and \(9{z^2}\)

Sol: Given two monomials are \(7{z^3}{\rm{ }}\& {\rm{ }}9{z^2}\) .

First, we multiply the coefficients. The coefficient of \(7{z^3}\) is 7, and the coefficient of \(9{z^2}\) is 9. After multiplying, we get \(7 \times 9 = 63\) .

Next, we will use the exponential rule to multiply the variables. Here, the variable parts are \({z^3},{\rm{ }}{z^2}\) . Multiplying these together, we get \({z^3} \times {z^2} = {z^5}\) because we added the exponent of the variable according to the exponent rule.

Therefore, the answer is \(63{z^5}\) .

Conclusion

Monomial multiplication is a method of multiplying two or more monomials at a time. Multiplying a monomial by another monomial yields a monomial as the product. Depending on the type of polynomial we use.

Practice questions

1. Find the factorization of the monomial \(10{y^3}\) .

Ans: \(2 \times 5 \times y \times y \times y\) .

2. Multiply \(2abc\)and \({a^2}b\).

Answer: \(2{a^3}{b^2}c\) .

3. Multiply \(8\) and \(6{y^3}\) .

Answer: \(48{y^3}\)

Frequently Asked Questions

1. How do you find the product of two monomials?

Ans: The constant coefficient of one monomial is multiplied by the constant coefficient of another monomial, and the variable is multiplied by one variable.

2. What are the rules in multiplying monomials?

Ans: We will multiply by the coefficient. Next, we’ll multiply the variables using the exponential rule wherever needed.

3. What is a monomial ?

Ans: Monomial   is an algebraic expression that contains only one term.