Tag: Math

Introduction

No matter how many sides there are in a polygon, the sum of all exterior angles is \({\bf{360}}^\circ \), and the sum of all internal angles is \(\;\left( {{\bf{n}} – {\bf{2}}} \right){\bf{180}}^\circ \) given that the number of sides is n.

Shapes are \(2 – \) dimensional and \(3 – \) dimensional; we have all seen them. A shape is also a polygon. A two-dimensional form having at least three sides is called a polygon. There might be four, five, or more sides. There are two types of polygons: regular polygons and irregular polygons. The sum of all external angles created in the polygon is the sum of measurements of the exterior angles. We shall explore exterior angles and the total of all exterior angles of a polygon in this subject.

Polygons

Polygons are \(2 – \) dimensional, plane figures with straight edges joining n points on a plane. The polygons are divided into two main sub-categories, i.e., Convex Polygons and Concave Polygons.

Concave Polygons

In these types of polygons, at least one of the diagonals passes outside of the polygon and at least one of the vertex is pointing inside the polygon, i.e., has an angle greater than  \(180^\circ \). Stars are one of the most common examples of concave polygons.

Convex Polygons

Convex polygons are the normal polygons, that have all the interior angles less than \(180^\circ \) , all the diagonals are always contained within the polygon.

Few of the most common examples of convex polygons are triangles and squares. Learn more about convex polygons in Class 6 Mathematics Video in Lesson no 14 Curves, Polygon.

Convex polygons are divided into \(2\) categories,

1. Regular polygons: These are the convex polygons that have all their sides of equal length, and the measure of each interior angle is equal.
2. Irregular polygons: These are the convex polygons that are not regular, i.e., their sides and angles are not all of equal measure.

Exterior angles

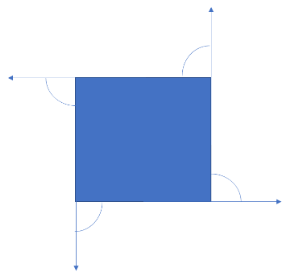
The external angle is the angle created outside of a polygon when one of its sides is expanded. It is created by the expanded side and the side next to it.

Properties of Exterior Angles of Polygons

Consider the many characteristics of the exterior angle of a hexagon, a polygon, for example. The attributes listed below provide information on the exterior angles:

• They are created outside of the specified figure.
• The internal and exterior angles that are created by the expanded side and the neighboring side are always added together.
• A regular polygon’s exterior angles are always equal to one another.

Sum of Exterior Angles of a Polygon: Geometrical Proof

Let’s take an example of hexagon, marking the vertices \(ABCDEF\) , so let’s move on the edge of this hexagon. Starting from \(A\) we move in a straight line, no turns happen until we reach vertex \(B\), where we turn slightly, the measure of the exterior angle at \(B\) , and once again move in a straight line until vertex \(C\) , we rinse and repeat this process until we are at our final stretch, i.e., edge \(FA\) . We have turned to the sum of all angles except A. Now at A we will turn once again and face the direction we started in, this gives us that we have turned a complete circle, i.e., 360, by rotating through each angle one by one.

\(A + B + C + D + E + F = 360^\circ \) 

Sum of Exterior angles =360°

Sum of Exterior Angles of a Polygon: Algebraic Proof

Let us consider a \(n – sided\) polygon. By Interior angle property we know that the sum of all interior angles is given by, \[180^\circ  \times (n – 2)\] 

Also, we know that each exterior angle forms a linear pair with the corresponding interior angle, thus the sum of all interior angles and the sum of all exterior angles should be equal to the sum of all the linear pairs formed.

180(n-2)+Sum of Exterior Angles=180n

Sum of Exteriror angles = 180n-180(n-2)

\( = 180n – 180n + 360\)

\( = 360^\circ \)

Summary

We examined the following salient characteristics in the aforementioned study:

Any sort of polygon’s exterior angles add up to \(360\).

Any form of polygon’s internal angles add up to (180\left( {n – 2} \right)\) .

A regular polygon’s exterior angles have a value of \(360/n\) .

A regular polygon’s internal angles are determined using the formula \(\frac{{180\left( {n – 2} \right)}}{n}\)  .

Online Tuition for Class 6 Maths

FAQs

1. What is the name of a polygon with \({\bf{12}}\) sides?
Ans. A polygon with \(12\) sides is known as a Dodecagon.

2. What is the measure of interior angles of a regular polygon of \({\bf{7}}\) sides?
Ans. The measure for interior angles of a n sided polygon is given by, \[\frac{{180\left( {n – 2} \right)}}{n}\] , substituting \(n = 7\) , we have,

\[\frac{{180\left( {7 – 2} \right)}}{7} = \frac{{900}}{7}\;\; \approx 128.57^\circ \]

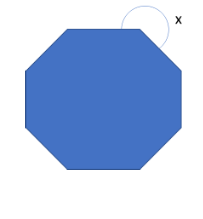
3. What is the measure of x in the following image?

Ans. In the given image, the angle x is the reflex angle of the interior angle of a regular octagon, thus we will find the interior angle of the octagon and subtract it from \(360^\circ \)

Interior angle\( = \frac{{180\left( {n – 2} \right)}}{n}\) 

Substituting \(n = 8\) ,

\(\begin{array}{*{20}{l}}{ = \frac{{180 \times 6}}{8} = 135^\circ }\\\;\end{array}\)

The reflex of this would be,

\[x = 360 – 135 = 225^\circ \]

Introduction

There are several instances when ratios and percentages are employed. The proportion and ratio ideas you acquired in earlier sessions are still fresh in your mind. On a milk packet, several milk components are listed in percentages. A certain ratio of finger millet flour and wheat flour is used to make ragi bread. To dilute a fruit juice concentrate, you must add water at a specific ratio. During the building process, a predefined ratio of cement, sand, and gravel is combined. We may calculate the percentage value of a certain amount by multiplying a ratio by \({\bf{100}}\) . In a number of computations, we also employ percentages. Let’s look at percentages and ratios in this article.

Ratios

How many times one quantity is compared to another is how a ratio is defined. The ratio should be interpreted as \({\bf{a}}\) to \({\bf{b}}\) .if it contains the values \({\bf{A}}\) and \({\bf{B}}\) in the ratio \({\bf{a}}{\rm{:}}{\bf{b}}\). This ratio may also be written as a fraction, \(\frac{{\bf{a}}}{{\bf{b}}}\) . The ratios \({\bf{1}}{\rm{:}}{\bf{2}}\), \({\bf{1}}{\rm{:}}{\bf{5}}\),and \({\bf{3}}{\rm{:}}{\bf{4}}\) are a few examples. 

A ratio has two parts, antecedent and consequent. The first number is called the antecedent and the second is the consequent.

Percentage

The ratio of one amount to another in terms of \({\bf{100}}\) is known as a percentage. It is a number without dimensions. The % sign is used to denote percentages.

Conversion between Ratio and Percentage

The formula below can be used to change a ratio into a percentage.

\(\%  = {\bf{Ratio}} \times {\bf{100}}\)

We may use the formula below to change a percentage into a ratio.

\({\bf{Ratio}} = \frac{{{\bf{Percentage}}}}{{{\bf{100}}}}\)  

Steps to Convert Data into Ratios and Percentage

Step one is to calculate the ratio of the questioned item to the total number of items.

Second step is format the ratio as a fraction.

Multiplying the fraction by \({\bf{100}}\) is step three.

Step four is to evaluate the percentage number by simplifying.

Example: Let there be \({\bf{28}}\) men and \({\bf{22}}\) women in a group of volunteers for a food camp drive.

Then the total number of volunteers is \({\bf{50}}\) .

We will find the ratio of men to women,

Ratio\( = {\rm{ }}{\bf{Men}}:{\bf{Women}}{\rm{ }} = \frac{{{\bf{Men}}}}{{{\bf{Women}}}} = \frac{{{\bf{28}}}}{{{\bf{22}}}} = \frac{{{\bf{14}}}}{{{\bf{11}}}} = {\bf{14}}:{\bf{11}}\)

Ratio of Men and Women to total is,

Ratio of Men \( = \frac{{{\bf{Men}}}}{{{\bf{Total}}}} = \frac{{{\bf{28}}}}{{{\bf{50}}}} = \frac{{{\bf{14}}}}{{{\bf{25}}}} = {\bf{14}}:{\bf{25}}\)

Ratio of Women\( = \frac{{{\bf{Women}}}}{{{\bf{Total}}}} = \frac{{{\bf{22}}}}{{{\bf{50}}}} = \frac{{{\bf{11}}}}{{{\bf{25}}}} = {\bf{11}}:{\bf{25}}\)

Finding the percentage of Men and Women respectively,

\(\% \) of Men\( = \frac{{{\bf{Men}}}}{{{\bf{Total}}}} \times {\bf{100}} = \) Ratio of Men\( \times {\bf{100}}\)

\( = \frac{{{\bf{14}}}}{{{\bf{25}}}} \times {\bf{100}} = {\bf{56}}\% \)

\(\% \) of Women\( = \frac{{{\bf{Men}}}}{{{\bf{Total}}}} \times {\bf{100}} = \) Ratio of Women\( \times {\bf{100}}\)

\( = \frac{{{\bf{11}}}}{{{\bf{25}}}} \times {\bf{100}} = {\bf{44}}\% \) 

Applications of Ratio and Percentage

• When combining two ingredients, ratios can be used. For instance, combining two different types of wheat and creating solutions with various liquids.
• Government authorities employ percentages when making some crucial choices, such those regarding assistance programms.
• More data may be simply understood and interpreted by us.
• Percentages are used by researchers to compare data.
• In order to calculate profit and loss and to understand how the shares of various stakeholders in a firm contribute, businesspeople utilize percentages.
• When developing a township or building a home, engineers allocate regions using percentages.

Difference between Ratio and Percentage

Ratio	Percentage
How many times one quantity is compared to another is how a ratio is defined. The ratio should be interpreted as a to b if it contains the values A and B in the ratio a:b.	The ratio of one amount to another in terms of 100 is known as a percentage. It is a number without dimensions. The % sign is used to denote percentages.
Ratios are comparisons between two parts of the same thing.	The percentage represents the part of the whole in terms of 100 parts, i.e., the number of sections the part has if the whole is divided into 100 sections.
Example: 1:2,  3:5 and 7:4, etc.	Example: 50%, 20% and 125% etc.

Interesting Facts

• The ratio of the Earth’s diameter to the Sun’s is \({\bf{1}}:{\bf{108}}\) .
• To change one currency into another, one uses ratios.
• The ratio between the heights and bases of similar triangles is \({\bf{1}}\) .

Solved Examples

Example: Find the ratio of Ravi and Suraj’s income, if Ravi earns \({\bf{40}}\% \) more than Suraj.
Ans: Let Suraj’s income be \({\bf{x}}\) .

Then Ravi’s income \( = {\bf{x}} + {\bf{40}}\% {\rm{ }}{\bf{of}}{\rm{ }}{\bf{x}}\)

\( = {\bf{x}} + \frac{{{\bf{40}}}}{{{\bf{100}}}}{\bf{x}} = \frac{{{\bf{140x}}}}{{{\bf{100}}}} = \frac{{{\bf{7x}}}}{{\bf{5}}}\)

Then the ratio of Ravi’s and Suraj’s income = Ravi’s Income: Suraj’s Income

\( = \frac{{{\bf{7x}}}}{{\bf{5}}}:{\bf{x}}\) 

\( = {\bf{7}}:{\bf{5}}\) 

Summary

In this article, we have learned about ratios and percentages. A ratio is the proportion of one quantity to another. The ratio of one quantity to another, stated in terms of \({\bf{100}}\) , is known as a percentage. For comparing amounts, we employ percentages as well as ratios.

Frequently Asked Questions

1. What are equivalent ratios?

Ans. Equivalent ratios are defined as the ratios comparing two different pair of quantities which have the same overall value, these ratios do not look the same on the first view, but on some mathematical manipulations they become exactly the same.

\({\bf{1}}:{\bf{2}},{\bf{2}}:{\bf{4}},{\bf{3}}:{\bf{6}}\) are all equivalent ratios to each other.

2. Which is more important, ratios or percentages?

Ans. To compare quantities with the whole, we use percentages and to compare two parts of the same thing we use ratios. Both have their own different use, and both are equally important for that. But we cannot compare quantities using percentages if the whole quantity is not given to us, but we can directly compare ratios to compare two parts without the knowledge of the whole. Which is why the ratios are slightly more important than percentages while comparing quantities. Whereas in practicality percentage are more easier to understand than ratios, which is why percentages are seen more often in real life examples, such as a discount of \({\bf{25}}\% \) is easier to interpret rather than saying a discount of \(\;{\bf{1}}:{\bf{4}}\).

3. What are proportions?

Ans. Proportions are a comparison between two ratios that are comparing two different pairs of quantities. They are represented by the symbol, ‘\(::\)’.

Introduction

An expression made up of variables, constants, coefficients, and mathematical operations like addition, subtraction, etc. is known as an algebraic expression. Algebraic expressions have several uses, including describing real-world issues and solving various and difficult mathematical equations, calculating income, cost, etc. There are two categories of words in algebra: like terms and unlike terms. Unlike terms are merely the opposite of like terms in that they do not share the same variables and powers. Like terms are those that have the same variables and powers.

Algebraic Expressions

An expression made up of variables, constants, coefficients, and mathematical operations like addition, subtraction, etc. is known as an algebraic expression. A variable is a symbol without a predetermined value. A term is either a variable, a constant, or both joined by mathematical operations. A coefficient is a quantity that has been multiplied by a variable and is constant throughout the whole problem. Based on a variety of terminology, there are three primary categories of algebraic expressions: monomial, binomial, and polynomial. Terms can also be divided into similar and dissimilar terms.

Also see: Online Tuition for Class 6 Maths

Terms in algebra

A term can be a number, a variable, the sum of two or more variables, a number and a variable, or a product of both. A single term or a collection of terms can be used to create an algebraic expression. For instance, \({\bf{2x}}\) and \({\bf{5y}}\) are the two terms in the expression \({\bf{2x + 5y}}\) .

A mathematical expression has one or more terms. A term in an expression can be a constant, a variable, the product of two variables \({\bf{\left( {xy} \right)}}\) or more \({\bf{\left( {xyz} \right)}}\) , or the product of a variable and a constant \({\bf{\left( {2x} \right)}}\) , among other things.

Also Read: Terms of an Expression

Terms in an algebraic expression

A term is a group of numbers or variables that have been added, subtracted, divided, or multiplied together; a factor is a group of numbers or variables that have been multiplied; and a coefficient is a number that has been multiplied by a variable. Three terms, \({\bf{9}}{{\bf{x}}^2}\) ,\({\bf{x}}\)  , and \({\bf{12}}\), make up the expression \({\bf{9}}{{\bf{x}}^2}\)+\({\bf{x}}\) + \({\bf{12}}\)

By drawing this conclusion, it is clear that an expression is made up of a number of terms, variables, factors, coefficients, and constants.

Types of Terms 

There are different types of terms in algebraic expressions,

Variables

These types of terms are usually represented by an symbol (most commonly its english alphabets), like \({\bf{x}}\), \({\bf{y}}\), \({\bf{z}}\), \({\bf{a}}\), \({\bf{b}}\), etc. these symbols are there to represent unknown arbitrary values, hence the name ‘variables’ (since their values can vary).

Coefficient

These are not a type of a term but rather a part of a term that contains variables, coefficients are the numbers that are in multiplication with variables.

Constants

These terms are the numbers separate from the variables, and as the name suggest, they are a constant number, i.e., they are fix and never change unless they are under an operation with another constant term.

Like and Unlike Terms

Like terms in algebra are the kinds of terms that share the same kinds of variables and powers. There is no requirement that the coefficients match. When a term has two or more terms that are unlike terms, it means that those terms do not share the same variables or powers. Before there is power, the order of the variables doesn’t matter. Consider the example of similar and dissimilar terms.

Like Terms: \({\bf{3x}}\), \({\bf{-5x}}\) are like terms

Unlike Terms:\(\;{\bf{2}}{{\bf{x}}^3},{\bf{7}}{{\bf{x}}^2}\)  and \({\bf{5y}}\)  are all unlike terms.

Like Terms

Terms with the same kinds of variables and powers are referred to as like terms. It is not necessary to match the coefficients. The coefficient could differ. To obtain the answer, we can simply combine like terms, or we can simplify the algebraic expressions. In terms of the same types of variables and powers, the results are very easily obtained in this way.

The evaluation of straightforward algebraic puzzles is an example of similar terms.

Unlike Terms

In algebra, unlike terms are those terms that do not share the same variables and cannot be raised to the same power.

For instance, in algebraic expressions, \({\bf{4x}} – {\bf{3y}}\) are unlike terms. because \({\bf{x}}\) and \({\bf{y}}\) are two different variables. Due to the lack of \({\bf{x}}\) and \({\bf{y}}\) values, it cannot be simplified.

Summary

An expression made up of variables, constants, coefficients, and mathematical operations like addition, subtraction, etc. is known as an algebraic expression. Coefficients, constants, and variables are a few of the key words in the context of algebraic expressions. Similar terms are those in algebraic expressions that are constants or involve similar variables raised to similar exponents. In algebraic expressions, unlike terms are those terms that do not share the same variables or that share the same variables but have different exponents. Algebraic expressions are all polynomials, but not all algebraic expressions are polynomials. Polynomials are algebraic expressions without fractional or non-negative exponents. Algebraic expressions include fundamental identities that are used in the subject.

Tips to Prepare for Class 6 Maths

FAQs

What are polynomials?

Polynomials are algebraic expressions with more than \({\bf{2}}\) terms and the variables have non-negative integer exponents.

What is a quadratic equation?

A quadratic equation is a polynomial equation, with maximum exponent on a variable being \({\bf{2}}\).

What is a term in an algebraic expression?

A term can be a number, a variable, the sum of two or more variables, a number and a variable, or a product of both. A single term or a collection of terms can be used to create an algebraic expression.

Introduction

In geometry, an angle is made when two rays are joined at the same location. The common point is referred to as the node or vertex, while the two rays are known as the arms of the angle. We use the symbol “\(\angle \)” to represent an angle. The word “angle” has its roots in the Latin word “Angulus”, before talking about congruent angles, let’s define the term. In geometry, two figures are said to be congruent if their size and shapes are the same. That suggests that they will completely overlap if we stack one figure on top of the other. These figures may be line segments, polygons, angles, or 3D objects.

Congruent Angle Construction

Corresponding angles are always congruent on congruent figures. Two situations are there while learning about the construction of congruent angles in geometry. They are
• Any measurement can be used to create two congruent angles.
• making a new angle that is comparable to the one already there
Let’s look at two angles that are congruent with each other.

In the figure above, the angles are equal in size (\({100^\circ }\) each). They might completely encircle one another. As a result, both of the above angles satisfy the concept of congruent angles.

The symbol \(\angle 1 \cong \angle 2\) represents the congruence of two angles.

Angle Congruence Theorems

Many theorems are built on the concept of congruent angles. The congruent angles theorem allows us to easily assess whether two angles are congruent or not. The following are the theorems:

• The vertical angle theorem
• The corresponding-angles theorem
• The alternate-angles theorem
• Congruent supplement theorem
• Congruent complements theorem

Let’s talk about how these theorems are stated. Different theorems can be used to demonstrate if two or more angles are congruent. The following are the theorems:

The vertical opposite angle theorem

If two lines intersect each other, then the vertically opposite angles are equal.

Congruent Complements Theorem

The next theorem, the congruent complements theorem, states that if two angles are complements of the same angle, then the two angles are congruent.

Congruent Supplements Theorem

According to the Congruent Supplements Theorem, two angles are congruent if they are supplements of the same angle.

The alternate interior angles theorem

This theorem states that the alternate interior angles are equivalent if a transversal intersects two parallel lines.

The alternate exterior angles theorem

This theorem states that the angles formed on the outer side of the parallel lines and opposite sides of the transversal, when a transversal joins two parallel lines, have to be equivalent.

The theorem of Corresponding Angles

If a transversal meets two parallel lines, the corresponding angles that result are congruent.

Summary

This article showed us that a pair of angles cannot be congruent unless their measurements are equal. The statements of congruence of vertical angles theorem, corresponding angles theorem, alternate angles theorem, congruent supplements theorem, and congruent complements theorem were the next ideas we learned. We next discussed a few examples of congruent angles. We also learned how the angles are congruent based on these theorems. When two unknown angles are regarded as congruent, as well as how to calculate an angle’s measure, were both covered. Finally, we solved several cases that illustrated the concept of congruence of angles.

1. What is an angle? What are the measuring units of angles, and what is the relation between them?

Ans. An angle is the elevation of one line from another. Angles are measured in two main unit systems, i.e., the degree system and the radian system. The degree system has 2 sub-divisions, minutes and seconds. 1 complete circle is 360 degrees, 1 degree has 60 minutes and 1 minute has 60 seconds, the degree system angles are always represented by whole numbers and any fractional part is moved on to the next subdivision. Whereas the radian system has no subdivisions and can be represented in whole numbers, fractions and decimals. In the radian system, 1 complete circle is \(2\pi {\text{ rad}}\).

\[{360^\circ } = 2\pi {\text{ rad}}\]

\[{1^\circ } = \frac{\pi }{{180}}{\text{ rad}}\]

\[1{\text{ rad}} = {\frac{{180}}{\pi }^\circ }\]

2.What do you mean by congruent angles?

Ans. An angle is said to be congruent to another angle if the two angles are equal in measure.

3.Are the following two angles congruent?

Ans. Two angles are congruent if they are equal in measure, in the following image, the 1st angle, by the vertically opposite angles property, is a right angle. For, the second angle, using the corresponding angles property we can say that the angle adjacent to it is also a right angle. Now using the linear pairs,

\[{90^\circ } + \angle 2 = {180^\circ }\]

\[\angle 2 = {90^\circ }\]

Hence, the 2nd angle is also a right angle. Thus, the two angles are congruent.

Want to dive deeper into the topic of congruence? Check out our article on “Congruence for Triangles“

Introduction

The definition of a rational number is a fraction of two numbers in the form \(\frac{p}{q}\), where p and q can both be integers but q cannot be equal to 0. Rational numbers include whole numbers, integers, and numbers with terminating decimals. Although rational numbers need not necessarily be fractions, any fractions can be rational numbers. The area of mathematics that deals with symbols and variables are called algebra. Natural numbers, Integers, 0, and other types of numbers are all included in rational numbers. Positive and negative numbers are both part of integers. Therefore, we can divide rational numbers into positive rational numbers and negative rational numbers. Positive rational numbers include, for instance, \(1,\frac{3}{16},\frac{25}{2}\), etc. These are examples of negative rational numbers: \( – 3, – \frac{1}{2}, – \frac{5}{3}\), etc.

Rational Numbers

The definition of a rational number is a fraction of two numbers in the form \(\frac{p}{q}\), where p and q can both be integers but q cannot be equal to 0. Rational numbers include whole numbers, integers, and numbers with terminating decimals. Although rational numbers need not necessarily be fractions they can be converted into one, all fractions are rational numbers.

Positive and Negative Rational Numbers

Those rational numbers that have both positive or negative numerators and denominators are known as positive rational numbers. Positive numbers that follow logic are always bigger than zero. For instance, when we divide \(\frac{8}{9}\), we obtain 0.88, which is more than 0, indicating that \(\frac{8}{9}\) is a positive rational number.

Those rational numbers that are negative because their numerators and denominators have opposite signs are known as negative rational numbers. Positive irrational numbers are never greater than zero. For instance, \( – \frac{{12}}{{13}}\) yields -0.92, which is both lower than 0 and a negative rational integer.

Positive Numbers

The number line can also be used to represent positive numbers. According to the illustration below, the numbers that are on the right side of the number line are thought of as positive numbers. Positive numbers are those whose value is consistently higher than zero.

Note: When a number is left unsigned, it is considered to be positive. For instance, the positive integers 45 and +45 are identical and both 45.

Negative Numbers

Similar to the positive numbers, the number line can also be used to represent negative numbers. According to the illustration below, the numbers that are on the left side of the number line are thought of as negative numbers. Negative numbers are those whose value is consistently higher than zero.

Positive, 0 and negative rational numbers are the three subcategories of rational numbers.

A rational number is positive if both the numerator and the denominator have the same sign, such as both being positive or both being negative, and it is negative if the numerator is negative and the denominator is positive or vice versa.

Take an example of \(\frac{3}{5}\) and \(\frac{{ – 3}}{{ – 4}}\) they are both positive since the sign of both numerator and denominator are the same in the respective numbers, whereas \(\frac{{ – 3}}{4}\) and \(\frac{4}{{ – 5}}\) are both negative since the signs in numerator and denominator are opposite.

Algebra of Rational numbers

Rational Numbers like all the other number categories under the real number have four basic binary operations, i.e, addition, multiplication and the inverse operations subtraction and division.

Addition and Multiplication of Rational numbers have the following properties,

Closure Property

Addition and Multiplication of rational numbers is closed, i.e., when two rational numbers are operated with these operations the result is always rational number.

Associative Property

Addition and Multiplication of rational numbers is associative, i.e., the order of operations does not change the result when the same operation is repeated between 3 or more numbers. Mathematically, for three rational numbers a, b and c

\[a + (b + c) = (a + b) + c{\text{ and }}a \cdot (b \cdot c) = (a \cdot b) \cdot c\]

Existence of Identity Property

The Identity element is known as the element which when operated with any other element, has no effect on it. For Addition of rational numbers, 0 is the identity element, and for multiplication it is 1.

Mathematically,

\[a + 0 = 0 + a = a{\text{ and }}a \cdot 1 = 1 \cdot a = a\]

Existence of Inverse Property

The Inverse of an element is known as the element which when operated with the first element, results in the identity. Rational numbers have additive inverse for all the numbers, and they are their negative counterparts, such as for 3 it is -3, for \(-\frac{5}{6}\) it is \(\frac{5}{6}\). For multiplication however, not all rational numbers have inverse, 0 is the rational number which does not have a multiplicative inverse, because by definition multiplicative inverse of a rational number \(a\) would be \(\frac{1}{a}\), but by the definition of rational numbers, 10 is not a rational number.

Commutative Property

Addition and Multiplication of rational numbers is associative, i.e., the order of element does not change the result. Mathematically, for two rational numbers a and b,

\[a + b = b + a{\text{ and }}a \cdot b = b \cdot a\]

Summary

In this article we learned about Rational numbers, positive and negative rational numbers. A rational number is defined as the number which can be represented by the form, \(\frac{p}{q}\) where p and q are coprime integers and \(q\ne 0\). The rational numbers, just like integers, can be divided into 3 categories i.e., positive, negative and 0. Positive rational numbers are those that are greater than 0, and negative are the ones that are smaller. The positive and negative rational numbers are represented on right and left sides of the number line respectively.

FAQs

What are Rational numbers? How do you identify rational numbers in decimal form?

Ans. Rational numbers are defined as the numbers which can be represented by the form, \(\frac{p}{q}\) where p and q are coprime integers and \(q \ne 0\). In decimal form, the numbers that have either terminating decimal expansion or if non-terminating then, repeating decimal expansion are rational numbers.

What is Rule for identifying positive and negative rational numbers from their fractional form?

Ans. There is one simple rule to identifying positive and negative rational numbers from fractional form

• If the numerator and denominator have the same sign, both either positive or negative, then the number as a whole is positive.
• If the numerator and denominator have different signs, numerator positive and denominator negative or vice versa, then the number as a whole is negative.

What are the numbers that are not rational called? What is the general identification of those numbers in the decimal form?

Ans. The real numbers that are not rationals, i.e., they cannot be represented in the form, \(\frac{p}{q}\) where p and q are coprime integers and \(q \ne 0\), are known as Irrational numbers. These are the numbers whose decimal expansion has infinite digits after the decimal, and they never repeat the same pattern.

Introduction

Only when two figures have the same size and shape, including their sides, points, angles, etc., can they be said to be congruent. 

1. Two circles should have the same diameter if they are congruent. 
2. If the sides and angles of two triangles are the same, they are said to be congruent. 
3. If the corresponding sides of two rectangles are equal, they are said to be congruent. 
4. If two squares have sides of the same length, they are said to be congruent.

If two shapes are equivalent to one another in all conceivable ways, they are said to be congruent. Congruent figures in mathematics are those that share the same size and shape. The 2-D and 3-D figures are both consistent with each other. However, this article will only discuss the congruence of plane figures. 

Figures that are consistent in size and shape are said to be congruent. Congruence is the name given to the relationship between two congruent figures. It is indicated by the symbol “≅“.

Plane Figures

A plane shape is a closed, 2-D, or flat figure. Different plane shapes have various characteristics, such as various vertices. A vertex is the point where two sides meet, and a side is a straight line that is part of the shape.

The following figures show some of the basic plane shapes: triangles, squares, rectangles, and circles.

Congruence of Plane figures

A geometric figure with no thickness is called a plane figure. Some of the plane figures include line segments, curves, or a combination of both line segments and curves. The sides of the plane figures are the straight lines or curves  that make them up.

If two plane figures, such as line segments, angles, and other figures, are similar in size and shape, they are said to be congruent. Congruence of plane figures is the name of the relationship in use.

Congruent Figures

Congruent figures are geometric objects that share the same size and shape in mathematics. The two figures are equal to one another and are referred to as congruent figures when you transform one figure into another by a series of rotations and/or reflections.

Congruence of Lines

If two line segments are of the same length, they are said to be congruent. They don’t have to be parallel, though. They are flexible and can be in any position or orientation. The separation between two points determines the length of a line segment.

Congruent Line Segments

A pair of equal-length line segments makes up the congruent segment. An exact starting point and ending point define a straight line segment. Its beginning and end points are known, so its length can be calculated. Congruent line segments can, but are not required to, be parallel, perpendicular, or at any other particular angle. 

In geometry, a line segment is a fundamental figure that is created by joining any two points on a plane figure. Line segments also make up the sides of the plane figures. Two line segments are said to be congruent if their lengths are the same. In other words, two line segments have equal lengths if they are congruent.

Rules of Congruence for Triangles

There are 5 basic rules of congruence:-

Side Side Side

Side Side Side or also known as SSS congruence criteria states that if  the three sides of one triangle are equal to the corresponding three sides of another triangle, then the triangles are congruent.

Side Angle Side

Side Angle Side or also known as SAS congruence criteria states that if two sides and the included angle of one triangle  are equal to the corresponding two sides and the included angle of another triangle , then the triangles are congruent.

Angle Side Angle

Angle Side Angle or also known as ASA congruence criteria states that if  two angles and the included side of one triangle are equal to the corresponding two angles and the included side of the another triangle,  then the two triangles are congruent.

Angle Angle Side

Angle Angle Side or also known as AAS congruence criteria states that if two angles and a side not common to the two angles of one triangle are equal to the corresponding angles and side of another triangle, then the triangles are congruent.

Right angle Hypotenuse Side

Right angle, Hypotenuse & Side or RHS congruence criteria only applies to right triangles, it says that in two right triangles if  the hypotenuse and one  side of a triangle are equal to the hypotenuse and the corresponding side of the other triangle, , then the triangles are congruent.

Summary

In this article the topic of congruence is discussed in detail. If two figures share the same shape and size, they are said to be congruent; alternatively,  a figure  is said to be congruent to its mirror image as they share the same shape and size. Figures drawn on a plane or other flat surface are referred to as “plane figures.” In geometry, a plane is a flat surface that can go on forever in all directions. It has infinite width and length, no thickness, and curvature as it is stretched to infinity.

This article also shines a light on the topic of Rules of Congruence for triangles. There are 5 basic congruence criteria.

Frequently Asked Questions

1. What do you mean by congruence?
   Ans. Congruent figures are geometric objects that share the same size and shape in mathematics. The two figures are equal to one another and are referred to as congruent figures.
   
2. Are all squares congruent?
   Ans. No, all squares are not congruent, since for congruence two figures must have all of their quantifying dimensions  equal, that includes all the sides and all the angles. All squares have the same angles, but their side lengths may be  different, hence they aren’t congruent.
   
3. Is AAA a criteria for congruence of triangles?
   Ans. No, AAA is not a criteria for congruence because even if all the angles of two triangles are correspondingly equal, that necessarily does not mean that they have the same side length, for example two equilateral triangles of sides 3cm and 5cm, they both have the same 60-60-60 angle but they are not congruent because their sides are of different lengths.
   
4. Is a Rhombus of side length 4cm congruent to a square with side 4cm?
   Ans. We know that both rhombus and square have the property that all their sides are of the same length. But a rhombus does not necessarily have the same angles, whereas by definition a square has all its angles 90 degrees. Hence, no, a rhombus of side length 4cm is not necessarily congruent to a square of side length 4cm.

   Also Read: Congruence of Angles

Introduction

If all three angles and three sides of one triangle are the same size and dimension as the corresponding angles and sides of the other triangle, then the two triangles are said to be congruent.

The size and shape of any two congruent triangles are the same. Angles in one triangle have a measure that is the same as angles in another triangle. The corresponding sides of the congruent triangles also have equal lengths. Triangles that are congruent with one another can reflect or rotate another.

Congruent Meaning

If two figures can be placed exactly over one another, they are said to be “congruent.”

Take bread example as an example. The bread slices are stacked one on top of the other so that the top slice completely encloses the bottom slice. When stacked on top of the other, every slice of bread is the same size and shape. When something is congruent, it must have the same size and shape. Mathematics uses the term “congruence” to describe when two figures have similar sizes and shapes.

Congruence of Triangles

A triangle is a closed 3-sided figure in geometry. A triangle is a closed polygon made up of three lines that intersect at three different angles. The two triangles are said to be congruent if all three corresponding sides are equal and all three corresponding angles have the same measure. The appearance of these triangles remains constant when they are moved, rotated, flipped, or turned. If the triangles are moved, they must be superimposed to be congruent. As a result, if the triangles’ corresponding sides and angles are equal, the triangles are congruent. Thus, along the corresponding sides and angles, the congruent triangles can be stacked one on top of the other.

Online Coaching Maths Tuition Classes 7 Are The Best Way To Go

Congruence Criteria for Triangles

Five triangle congruence rules can be used to determine whether a given pair of triangles are congruent or not. The six dimensions allow for a perfect definition of any triangle. The particular triangle has three sides, as well as three angles. As a result, only three of the triangles’ six parts can be used to determine whether two triangles are congruent. The acronym CPCT stands for “Corresponding parts of Congruent triangles”. Triangles can be shown to be congruent, at which point the remaining dimension can be predicted without having to calculate the triangles’ missing sides and angles. The following lists the five triangle congruence rules.

• SSS (Side-Side-Side)
• SAS (Side-Angle-Side)
• ASA (Angle-Side-Angle)
• AAS (Angle-Angle-Side)
• RHS (Right angle -Hypotenuse-Side)

Note: ASA and AAS are not the same. Like ASA and AAS, SAS does not have any related counterpart like SSA, However, a variation of ASS exists for right triangles as RHS, where R is the angle and the other two, i.e., H and S, are sides.

Congruent Triangles Properties – CPCT

Congruent triangles have all their sides and angle equal, thus if two triangles are where we know all the properties of one and not the other, then we can find all the properties of the second triangle by simply comparing the corresponding parts in the first. Congruent triangles are most frequently referred to using the abbreviation CPCT. The term “Corresponding Parts of Congruent Triangles” is abbreviated as CPCT. It is a crucial characteristic of congruent triangles. Congruent triangles’ respective parts are always equal. The congruent triangle properties refer to this.

Types of Congruence

There are 5 types of triangle congruence criteria.

Side Side Side (SSS)

Side Side Side or also known as SSS congruence criteria states that if all three sides of two triangles are equal, then the triangles are congruent.

Side Angle Side (SAS)

Side Angle Side or also known as SAS congruence criteria states that if two sides and their included angles are equal in two triangles, then the triangles are congruent.

Angle Side Angle (ASA)

Angle Side Angle or also known as ASA congruence criteria states that if a side and two angles on it are equal in two triangles, then the triangles are congruent.

Angle Angle Side (AAS)

Angle Angle Side or also known as AAS congruence criteria states that if two angles and a side not common to the two angles are equal in two triangles, then the triangles are congruent.

Right angle Hypotenuse Side (RHS)

Right angle Hypotenuse Side or RHS congruence criteria only applies to right triangles, it says that in two triangles if they have a right angle, and their hypotenuses and one other side are equal in both triangles, then the triangles are congruent.

Summary

In this article, the topic of congruence is discussed in detail. If two figures share the same shape and size, they are said to be congruent; alternatively, if a figure shares the same shape and size as its mirror image, it is said to be congruent to its mirror image.

This article also shines a light on the topic of Rules of congruence for triangles. There are 5 basic congruence criteria, namely SSS, SAS, ASA, AAS, and RHS.

For more help, you can Refer to Lesson 23 congruence of Triangles in Math Class 7.

Frequently Asked Questions

1. What do you mean by Congruence?

Ans 1. Congruent figures are geometric objects that share the same size and shape in mathematics. The two figures are equal and are referred to as congruent figures.

2. Are all Squares Congruent?

Ans 2. No, all squares are not congruent, since for congruence two figures must have all of their quantifying dimensions must be equal, that includes all the sides and all the angles. All squares have the same angles, but their side lengths are different, hence they aren’t congruent.

3. Is AAA a criterion for the Congruence of Triangles?

Ans 3. No, AAA is not a criterion for congruence because even if all the angles of two triangles are equal, that necessarily does not mean that they have the same side length, for example two equilateral triangles of sides 3cm and 5cm, both have the same 60-60-60 angle, but they are not congruent because their sides are of different lengths.