Tag: Length

Introduction

The three dimensions of a cuboid are known as the length, breadth, and height, and the volume of the cuboid depends on these parameters. As is the norm, the volume is measured either in cubic units of length like \({cm^3}\), \({m^3}\),  etc., or we can measure the volume in units of litres and millilitres. The choice is a matter of convenience.

What is a Cuboid

A cuboid is a solid rectangular box with six faces, all of which are rectangles. The rectangles that lie opposite to each other are parallel while those that are adjacent intersect each other at right angles. You can think of a cuboid as a solid rectangle in three dimensions. The figure given below illustrates it better.

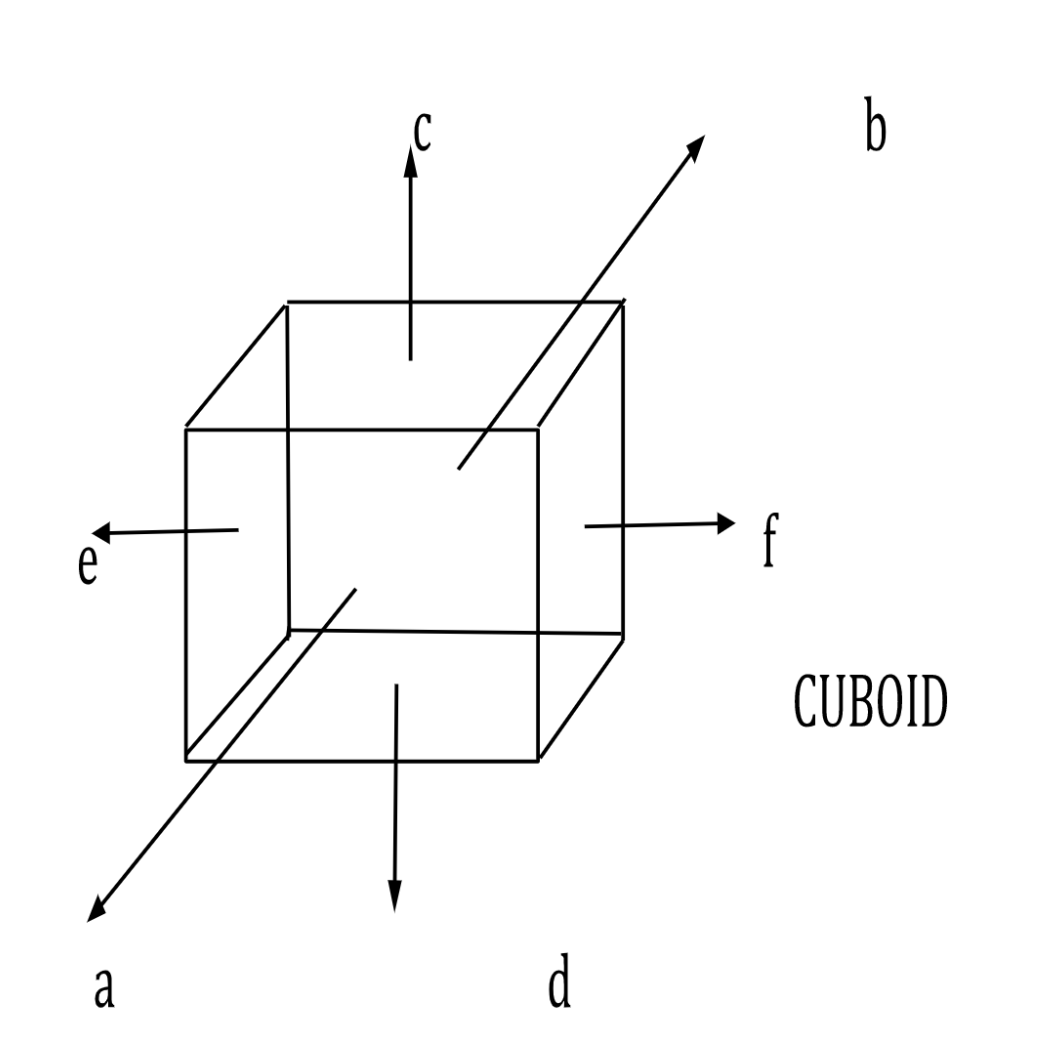
A cuboid

The cuboid shown above has six rectangular faces denoted as a, b, c, d, e, and f. The front and back faces, a and b respectively, are congruent rectangles that are parallel to each other. Likewise, the top and bottom faces, c and d respectively, lie parallel to each other and are congruent, just as the side faces e and f are parallel to each other.

What is the volume of a Cuboid?

As previously mentioned, the volume of a cuboid measures the space it occupies in three-dimensional space and is dependent on its dimensions. For a cuboid, the volume is simply the product of its length, breadth, and height. That is,

𝑉=𝑙𝑒𝑛𝑔𝑡h ×𝑏𝑟𝑒𝑎𝑑𝑡h× h𝑒𝑖𝑔h𝑡  

This volume can be measured in any unit of volume like \({cm^3}\), litres, millilitres, etc. The figure given below shows the 3 dimensions.

Cuboid dimensions

Notice how this formula also means that the volume equals the area of the base times the height of the cuboid. Thus, calculation of the area of a cuboid is a fairly easy task. However, it must be noted that the units must be consistent while performing any calculations. If the dimensions aren’t provided in the same units, we can end up with skewed and wrong results.

Also Read: How to Calculate the Volume of a Sphere

Solved Examples

1. A cuboid has dimensions 10 cm x 5 cm x 4 cm. Find its volume.

Solution

Given length = 10cm, breadth = 5cm, and height = 4cm.

We have the formula for the volume, which says that 𝑉=𝑙𝑏h 

. And since all measurements are provided in cm3 only, no unit conversions are required. Therefore,

𝑉=𝑙𝑏h 

𝑉=10×5×4 

𝑉=200  \({cm^3}\)

Therefore, the volume of the cuboid is 200 \({cm^3}\).

2. Given a cuboid with length, breadth, and height of 7m, 300cm, and 2m respectively, find its volume in cubic metres.

Solution

Given length = 7m, breadth = 300cm, and height = 2m, we need to calculate the volume. However, this time, one of the dimensions is provided in centimetres instead of metres and we will need to convert it before applying the formula. We know that

1 𝑚=100 𝑐𝑚 

∴300 𝑐𝑚=3 𝑚 

Now we can apply the formula we have.

𝑉=𝑙𝑏h 

𝑉=7×3×2 

𝑉=42  \({m^3}\)

Word Problems

1. How much water can be poured into a cuboidal tank that is 6m long, 5m wide, and 3m high?

Solution 

Given length = 6m, breadth = 5m, and height = 3m. All units are consistent, and we can directly apply the formula. Thus,

𝑉=𝑙𝑒𝑛𝑔𝑡h× 𝑏𝑟𝑒𝑎𝑑𝑡h × h𝑒𝑖𝑔h𝑡 

𝑉=6×5×3 

𝑉=90 \({m^3}\)

Therefore, the volume of the tank is 90 \({m^3}\).

Summary

This tutorial discussed the cuboid shape and its volume. We learned that the volume of a cuboid is simply the product of its dimensions, which include the length, breadth, and height.

Frequently Asked Questions

1. What is the shape of the face of a cuboid and how many faces does a cuboid have?

A cuboid is a solid rectangle, and it has six faces. Pairs of opposite faces are congruent to each other.

2. What is the difference between a cube and a cuboid?

A cube is a special type of cuboid whose length, breadth, and height are all equal, i.e., it has square faces. On the other hand, a cuboid has rectangular faces with differing length, breadth, and height.

3. What is the difference between the volume of a cube and the volume of a cuboid?

There isn’t much difference in the way volumes are calculated for the cube and the cuboid. In fact, the formula for the volume of a cube is 𝑉= \({a^3}\)

, which is basically the same as that for the cuboid since here, the length, breadth, and the height are all equal to a.

4. How many sides, faces, and vertices are there in a cuboid?

A cuboid has 12 sides, 6 faces, and 8 vertices.

Introduction

To measure the focal length, the distance of the object or image from the mirror, and the mirror’s magnification when studying the reflection of light by spherical mirrors and the generation of pictures by spherical mirrors, several sign conventions must be learned. A spherical mirror‘s pole, sometimes referred to as the origin or origin point, serves as the source of all signals. This sign convention is known as the New Cartesian Sign Convention.

Sign Convention for Reflection by Spherical Mirrors

The sign convention for the mirror was developed with the notion that items are always placed on the left side of the mirror, causing incident light to pass from left to right. For spherical mirrors, the following sign convention applies:

• From the pole, every measurement is taken.
• When measured in the direction of the incoming light, distances are thought of as positive; but, when measured in the opposite direction, they are thought of as negative.
• Upward values are positive and descending values are negative when measuring distances perpendicular to the main axis.

Sign Convention Diagram

Sign Convention for Concave and Convex Mirror

Concave Mirror Sign Convention

• The distance of the object seems to be negative since it is always in front of the mirror.
• The concave mirror’s focal length and radius of curvature are both viewed as negative since the focus and centre of curvature are in front of the concave mirror.
• The distance is determined as – (negative) when the image forms in front of the mirror and as + (positive) when it does so behind the mirror (positive).
• When an image is upright, height is positive; when it is inverted, height is perceived negatively.

Convex Mirror Sign Convention

• The object distance is displayed as negative since the object is always in front of the mirror.
• The radius of curvature and focal length are viewed as + (positive) in the case of a convex mirror since the centre of curvature and focus is located behind the convex mirror.
• Since convex mirrors always form an image behind a mirror, the image’s distance is considered to be positive.
• Since an upright image always forms when using a convex mirror, the image’s height is seen as positive.

Mirror Formula

The distance between an object’s main axis point and the mirror’s pole is referred to as the object distance and is presented by u. The image distance is the distance between a spherical mirror‘s pole and the location of an item on its primary axis and marked with v. Therefore, the formula for the focal length (f) in a spherical mirror can be expressed as                                                                                                                                                                                                      1⁄f = 1⁄u + 1⁄v

Summary

To understand the relationship between the object distance, its image distance, and focal length, the Sign convention is a crucial component of this topic. Additionally, due to the Cartesian system we utilise in the unique mirror sign convention, all mirrors have distinct signs for many variables. We put up a relationship between them using the mirror formula to gain a clearer image, and we can utilise this relationship to solve our numerical difficulties.

Frequently Asked Questions (FAQs)

1. Is the Object Distance Positive or Negative in the Concave Mirror?

Ans: A concave or convex mirror’s object distance is always negative because objects are always positioned on the left side of the mirror, and a spherical mirror’s sign convention dictates that distances to the left of the mirror are always negative. When an image forms on a concave mirror, the image distance v will be negative if it does so on the left side and positive if it does so on the right.

2. What is a Virtual Image?

Ans: Anything that is placed in front of a mirror produces an image. The image is a real image if the object’s light rays strike the mirror, reflect off of it, and then coalesce to form the image. If the image must be produced by extrapolating the reflected light beams backwards rather than converging, it is referred to as a virtual image. Any kind of mirror, whether concave, convex, or planar, may create a virtual picture. These pictures are displayed on the lens or the mirror.

3. What is the Sign Convention we use in the Concave Mirror?

Ans: The object’s symbol is interpreted negatively since it is constantly placed in front of the mirror. The focal length and radius of curvature have negative signs because the concave mirror‘s centre of curvature and focus are in front of it. An image’s height is seen positively while it is upright and negatively when it is inverted. When an image forms in front of the mirror, the distance is estimated as – (negative), and when it forms behind the mirror, the distance is calculated as + (positive) (positive).

Introduction

Atoms, which give all other matter in the universe its mass, volume, and resilience to survive changes in its physical state, are responsible for the matter’s mass and volume. Each type of matter, molecule, element, or even chemical, has a unique set of features that aid in understanding how that matter is used in everyday life. While the primary characteristics of matter are pressure, density, and volume, the primary characteristics of chemicals are toxicity, chemical stability, and the strength of their covalent bonds. As a result, there are many things to learn about the characteristics of each element and chemical complex.

What are Physical Properties?

As is common knowledge, every element and form of matter has unique characteristics. Physical property is any attribute that can be measured and that also describes an object’s physical condition. A physical state can change through time, which is referred to as a physical state shift. Physical characteristics can also be seen. Meaning that any changes in the physical stuff are readily seen. Without affecting the substance’s identity, these qualities may be identified. Contrarily, this is not true of chemical attributes because the substance changes as a result of identification.

Example of Physical Properties

Recognition and measuring the properties of matter depend upon certain aspects, even though it does not need to undergo any changes in its identity. For instance, if it involves measuring the amount or substance then it is extensive physical property (by appearance)

• Volume
• Mass
• Length
• Shape

If it is not dependent on the amount of substance, then it is intensive physical property (by observing its physical state in extreme temperature)

• Melting point
• Colour
• Boiling point
• Density

Measurement of Physical Properties

For scientific study, measurements of physical attributes are required. Quantitative measures, as the name implies, are used to carry out the task and based on the physical properties (either extensive or intensive), a measurement is made. The SI units are used to express the measurements. The various physical quantities, together with their corresponding symbols and SI units, are displayed in the table below.

Physical quantity	Symbols	Name of the SI unit	The Symbol for the SI unit
Length	l	metre	m
Mass	m	Kilogram	kg
Time	t	Second	s
Electric current	l	Ampere	A
Thermodynamic temperature	T	Kelvin	K
Amount of substance	n	Mole	mol
Luminous intensity	lv	Candela	cd

Physical Properties of Elements

The physical properties of materials are determined by performing intensive material characterizations. We already know that two or more molecules may be combined to form an element. As a result, knowing its qualities based on the number of atoms it contains is simpler. We may learn about a substance’s density, electrical stability, and capacity to tolerate intense heat to determine its melting and boiling points. Understanding the characteristics of the elements is essential since it is beneficial in many ways. We can determine which elements share a particular attribute and which do not. Iron and copper, for instance, have similar characteristics but distinct ones. i.e., they can both conduct electricity. They cannot, however, be exposed to damp air.

Physical Properties of Materials

We have understood the properties of elements, but what about materials? Materials are nothing more than things like metals, ceramics, and polymers. Their differing densities and thermal characteristics set them apart from one another. Among a material’s characteristics are,

• Thermal conductivity
• Resistivity
• Density
• Melting point
• Corrosion resistance

Three Physical Properties of Water

Even water, which is measured in litres, has physical characteristics. Other than being placed in the container to acquire their form and volume retention, they experience no physical changes. Water has distinct physical characteristics:

• Temperature
• Colour 
• Turbidity
• Taste
• Odour

Summary

Physical characteristics are observable, which means we can see them with our naked eyes. In contrast to chemical attributes, physical properties do not experience any changes to their physical state. There are two ways to observe physical qualities. Both extensive and intensive physical properties.

Frequently Asked Questions 

1. What is a Physical Change?

Ans: Except for one or more physical features, a substance’s chemical properties remain unchanged. We refer to this as a bodily transformation. In other words, a substance is capable of taking on any shape, size, or structural modifications. Physical changes also include state changes, such as going from a solid to a liquid or from a liquid to a gas. Cutting, bending, melting, freezing, boiling, and dissolving are a few of the processes that result in physical changes.

2. What are the Chemical Properties of Matter?

Ans: Chemical characteristics are the measurements or observations of a chemical substance. Chemicals contain certain characteristics that can only be identified when the substance transforms into another sort of substance. For research objectives, chemical characteristics are very useful in differentiating molecules. Reactivity, flammability, and corrosion are a few of the characteristics. Reactivity is defined as the capacity to interact with other chemical compounds. Flames and chemicals react rapidly. Thus, the flame characteristic of many chemicals may be identified.

3. How do bonds Affect Physical Properties?

Ans: Chemical bonds are the electrical forces that hold ions and atoms together during the formation of molecules. These chemical bonds are responsible for the physical properties of matter like hardness, structure, melting, and boiling points. They also influence other properties such as crystal symmetry and cleavage etc. It is more difficult to break apart bonds that are stronger than they are. Hardness, higher melting and boiling points, and less chance of expansion are all caused by stronger chemical bonds.

Introduction

If all three angles and three sides of one triangle are the same size and dimension as the corresponding angles and sides of the other triangle, then the two triangles are said to be congruent.

The size and shape of any two congruent triangles are the same. Angles in one triangle have a measure that is the same as angles in another triangle. The corresponding sides of the congruent triangles also have equal lengths. Triangles that are congruent with one another can reflect or rotate another.

Congruent Meaning

If two figures can be placed exactly over one another, they are said to be “congruent.”

Take bread example as an example. The bread slices are stacked one on top of the other so that the top slice completely encloses the bottom slice. When stacked on top of the other, every slice of bread is the same size and shape. When something is congruent, it must have the same size and shape. Mathematics uses the term “congruence” to describe when two figures have similar sizes and shapes.

Congruence of Triangles

A triangle is a closed 3-sided figure in geometry. A triangle is a closed polygon made up of three lines that intersect at three different angles. The two triangles are said to be congruent if all three corresponding sides are equal and all three corresponding angles have the same measure. The appearance of these triangles remains constant when they are moved, rotated, flipped, or turned. If the triangles are moved, they must be superimposed to be congruent. As a result, if the triangles’ corresponding sides and angles are equal, the triangles are congruent. Thus, along the corresponding sides and angles, the congruent triangles can be stacked one on top of the other.

Online Coaching Maths Tuition Classes 7 Are The Best Way To Go

Congruence Criteria for Triangles

Five triangle congruence rules can be used to determine whether a given pair of triangles are congruent or not. The six dimensions allow for a perfect definition of any triangle. The particular triangle has three sides, as well as three angles. As a result, only three of the triangles’ six parts can be used to determine whether two triangles are congruent. The acronym CPCT stands for “Corresponding parts of Congruent triangles”. Triangles can be shown to be congruent, at which point the remaining dimension can be predicted without having to calculate the triangles’ missing sides and angles. The following lists the five triangle congruence rules.

• SSS (Side-Side-Side)
• SAS (Side-Angle-Side)
• ASA (Angle-Side-Angle)
• AAS (Angle-Angle-Side)
• RHS (Right angle -Hypotenuse-Side)

Note: ASA and AAS are not the same. Like ASA and AAS, SAS does not have any related counterpart like SSA, However, a variation of ASS exists for right triangles as RHS, where R is the angle and the other two, i.e., H and S, are sides.

Congruent Triangles Properties – CPCT

Congruent triangles have all their sides and angle equal, thus if two triangles are where we know all the properties of one and not the other, then we can find all the properties of the second triangle by simply comparing the corresponding parts in the first. Congruent triangles are most frequently referred to using the abbreviation CPCT. The term “Corresponding Parts of Congruent Triangles” is abbreviated as CPCT. It is a crucial characteristic of congruent triangles. Congruent triangles’ respective parts are always equal. The congruent triangle properties refer to this.

Types of Congruence

There are 5 types of triangle congruence criteria.

Side Side Side (SSS)

Side Side Side or also known as SSS congruence criteria states that if all three sides of two triangles are equal, then the triangles are congruent.

Side Angle Side (SAS)

Side Angle Side or also known as SAS congruence criteria states that if two sides and their included angles are equal in two triangles, then the triangles are congruent.

Angle Side Angle (ASA)

Angle Side Angle or also known as ASA congruence criteria states that if a side and two angles on it are equal in two triangles, then the triangles are congruent.

Angle Angle Side (AAS)

Angle Angle Side or also known as AAS congruence criteria states that if two angles and a side not common to the two angles are equal in two triangles, then the triangles are congruent.

Right angle Hypotenuse Side (RHS)

Right angle Hypotenuse Side or RHS congruence criteria only applies to right triangles, it says that in two triangles if they have a right angle, and their hypotenuses and one other side are equal in both triangles, then the triangles are congruent.

Summary

In this article, the topic of congruence is discussed in detail. If two figures share the same shape and size, they are said to be congruent; alternatively, if a figure shares the same shape and size as its mirror image, it is said to be congruent to its mirror image.

This article also shines a light on the topic of Rules of congruence for triangles. There are 5 basic congruence criteria, namely SSS, SAS, ASA, AAS, and RHS.

For more help, you can Refer to Lesson 23 congruence of Triangles in Math Class 7.

Frequently Asked Questions

1. What do you mean by Congruence?

Ans 1. Congruent figures are geometric objects that share the same size and shape in mathematics. The two figures are equal and are referred to as congruent figures.

2. Are all Squares Congruent?

Ans 2. No, all squares are not congruent, since for congruence two figures must have all of their quantifying dimensions must be equal, that includes all the sides and all the angles. All squares have the same angles, but their side lengths are different, hence they aren’t congruent.

3. Is AAA a criterion for the Congruence of Triangles?

Ans 3. No, AAA is not a criterion for congruence because even if all the angles of two triangles are equal, that necessarily does not mean that they have the same side length, for example two equilateral triangles of sides 3cm and 5cm, both have the same 60-60-60 angle, but they are not congruent because their sides are of different lengths.