Introduction
The frustum is made up of a combination of solids. The volume of frustum means the space required by the frustum. In the previous tutorial, we have seen that the volume of a combined solid is equal to the summation of the volume of individual solids. In this tutorial, we will learn the basic structure, properties, and formula to determine the frustum volume with solved examples.
What is Frustum?
The word “frustum” originated from the Latin word “morsel”. The frustum is a portion of a pyramid or a cone, which lies between one or two parallel planes cutting this. Consider a cone cut into two parts by a plane (parallel to the base). The base faces look like polygonal shapes, and the side faces look like trapezoidal shapes. The portion between the baseline and the parallel plain is known as a frustum (as shown in the figure). It is also known as a truncated cone. If the side lengths of the frustum are of equal length, then it is known as a uniform prism. The real-life examples of the frustum include drinking glasses, pyramids, buckets, some space capsules, etc.

What is the Volume of a Frustum?
The volume of the frustum is defined as the space occupied by the object (frustum). The unit of volume of a frustum is generally expressed in \(c{m^3}{\mkern 1mu} {\rm{,}}{m^3}{\mkern 1mu} or{\rm{,}}i{n^3}\). The volume of any frustum can be determined if the height and the area of the two bases are known to us. Hence, the following formula can be used to evaluate the volume of a frustum of any shape.

where V and H are the volume and height of any frustum, respectively. In addition, \({A_1}\ and \({A_2}\ refer to the area of two bases of the frustum.

where R = Radius of the lower base of the frustum
r = Radius of the upper base of the frustum
h = Distance from upper base to the apex of the cone
Let’s derive the above formula by two methods.
Method 1:
We can observe that the bases (lower and upper) of the frustum are of circular shapes.
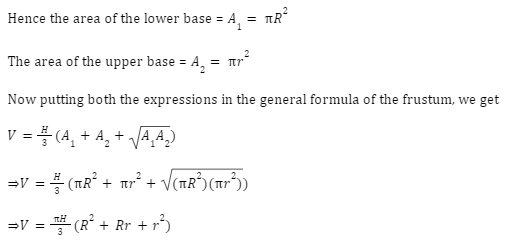
Method 2:


Expand your knowledge of mensuration with our 88guru’s online maths tuitions! Join now to learn about the fascinating concept of “Volume of a Frustum” and other interesting topics. With our 4-day free trial, you can experience the quality of our teaching before committing. Don’t miss out on this opportunity to enhance your mathematical skills!
Solved Examples
Example 1:
The side length of the bases of a frustum are 9 cm and 4 cm. Both bases are square. The height of the frustum is 6 cm. Find the volume of the frustum.
Solution:

Example 2:
The height and radius of the large base of a frustum are 15 cm and 5 cm, respectively. The radius of the small base is 2.5 cm. Evaluate the volume of the frustum.
Solution:

Summary
The present tutorial gives a brief introduction about the volume of a frustum. The basic definition of the frustum and some real-life examples are illustrated. In addition, the formulae and their derivation to determine the volume of a frustum have been depicted in this tutorial. Moreover, some solved examples have been provided for better clarity of this concept. In conclusion, the present tutorial may be useful for understanding the basic concept of the volume of a frustum.
Frequently Asked Questions
1. What do you mean by the frustum of a cone?
If a cone is cut into two parts by a horizontal plane, then the lower part of the cone (opposite to the apex) is known as the frustum of a cone.
2. What is the formula to determine the curved surface area of the frustum?
The curved surface area of the frustum can be determined by using the following formula.
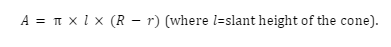
3. What are the possible shapes of the base of the frustum?
The base of the frustum can be of any shape. They may be of square, rectangular, or circular shape.
4. Give some examples of the frustum.
Some real-life examples of frustum include table lamps, buckets, glasses, glass tumblers, etc.
5. What are the properties of a frustum?
The properties of a frustum are summarized below.
- The height of a frustum is the perpendicular distance between the two bases.
- Each element of a frustum of a cone is similar to the original cone.
Also Read:
Volume of Cube
Volume of a Pyramid