Introduction
It is important to understand prime numbers before we start figuring out how to find them. Numbers with only two factors, i.e., 1 and the number itself, are known as prime numbers. When we are given a number that is small, it is easy to figure out whether it is a prime number or not. However beyond two digits, the task becomes difficult and we have different tricks and theorems one can use.
In this article, we will discuss prime numbers as well as their identification, the consecutive prime formula, and also solve a few problems so you can better understand this concept.
What are prime numbers?
For a number to be prime, it should be a whole number divisible only by 1 or by itself. For instance, if we try to find the factors of 89, we will see that it is not divisible by any number other than 1 or itself and thus, is a prime number.
Here are a few properties of prime numbers:
- Any positive integer larger than 2 can be written as the sum of two prime numbers.
- Two prime numbers are always coprime.
- The only even prime number is 2 and all the remaining prime numbers are odd.
- The prime factors of each composite number are distinct.
How to identify if a number is prime
Since a prime number is only divisible by one or itself, an easy check for smaller numbers is to factorise them and check whether they have other factors. This involves the following steps.
Step 1: Find out the factors of the number in question.
Step 2: Determine how many does factors it has.
Step 3: If there is a total of more than two factors, the number isn’t prime.
For instance, 85 has a number of factors and as soon as you encounter the fact that it is divisible by 5, it is no longer prime. However, this method is not suitable for larger numbers since it becomes very time-consuming.
Let’s check 95 now. This time, we will utilise a clever trick that works as follows:
Step 1: Find the square root of the number given. In this case, it is \(\sqrt {95} = 9.74 \approx 9\) (we take the integer value).
Step 2: Select all prime numbers below the answer we have just derived (9) and see if they divided the number we are given.
Step 3: Upon doing so, we discover that 95 is divisible by 5 and thus, it is not a prime number.
Consecutive prime formula
While there is no general formula for giving us consecutive prime numbers, we can utilise a few tricks:
- Except for the 2 and 3, all prime numbers can be represented in the form \(6n \pm 1\), where n is a natural number.
- For prime numbers greater than 40, the following formula holds: Let n = 0, 1, 2,….., 39, then \({n^2} + n + 41\) gives us prime numbers.
Solved Examples
Example 1: Is 23 a prime number?
Solution: To check whether 23 is prime or not, we have two approaches:
Approach 1:
We can check whether it fits on the pattern of \(6n \pm 1\). If we put n = 4, we get \(6n – 1 = 23\) and thus, we can say it may be prime.
Approach 2:
We can factorise 23 and we see that it only has the factors 1 and 23. Thus, both approaches confirm that it is a prime number.
Example 2: Is 61 a prime number?
Solution: For prime numbers greater than 40, we use the formula we just discussed. Let \({n^2} + n + 41\), where n=0,1,2….,39
Upon solving, we find that if n = 4, we get the answer as 61 and thus, 61 is a prime number.
Example 3: Check whether 24 is a prime number.
Solution: We start by finding its prime factors
\(\begin{array}{l}\begin{array}{*{20}{l}}{24{\rm{ }} = {\rm{ }}1{\rm{ }} \times {\rm{ }}24}\\{24{\rm{ }} = {\rm{ }}2{\rm{ }} \times {\rm{ }}12}\\{24{\rm{ }} = {\rm{ }}3{\rm{ }} \times {\rm{ }}8}\end{array}\\24{\rm{ }} = {\rm{ }}4{\rm{ }} \times {\rm{ }}6\end{array}\)
Thus, 24 has numerous factors, including 1, 2, 3, 4, 6, 8, and 12. Thus, it is not a prime number.
Summary
- A whole number divisible only either by one or by itself is called a prime number.
- A prime number larger than one has only one prime factor, i.e., itself.
- Any positive integer greater than 2 can be written as a sum of two prime numbers.
- Two prime numbers are always coprime.
- 2 is the only even prime number.
- The most basic way to check whether a number is prime is to factorize it. If it has more than two factors, it is not a prime number.
- All prime numbers greater than 3 can be written in the form \(\;6n \pm 1\), where n is a natural number.
- Prime numbers greater than 40 can be written in the form \({n^2} + n + 41\), where n goes from 0 to 39.
Frequently Asked Questions
1. What are prime numbers?
Numbers that can only be divided by one or by themselves are called prime numbers.
2. What is the formula to calculate prime numbers above 40?
Prime numbers greater than 40 can be written in the from \({n^2} + n + 41\), where n goes from 0 to 39.
3. Is it possible that a number is both composite and prime?
No. The conditions of being prime and being composite are contradictory. However, the number 1 is said to be neither prime nor composite.
4. What are composite numbers?
Composite numbers are the opposites of primes. These are numbers which have more than two factors.
5. State some properties of prime nunumbers.
- Two prime numbers are always coprime.
- Any positive integer greater than 2 can be written as the sum of two prime numbers.
- A prime number is a positive integer greater than 1.
- It is only divisible by 1 and itself.
- Every prime number has exactly two distinct factors, namely 1 and the prime number itself.
- There are infinitely many prime numbers.
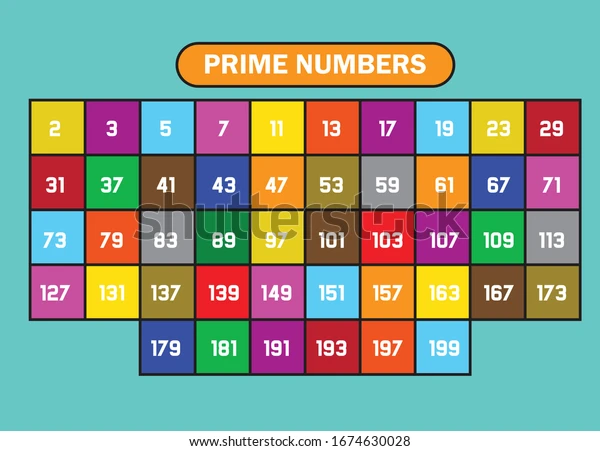
- The first five prime numbers are 2, 3, 5, 7, and 11.
- Every integer greater than 1 can be expressed as a product of primes, and this factorization is unique up to the order of the factors. This is known as the Fundamental Theorem of Arithmetic.
- Prime numbers are important in number theory and have applications in cryptography and other areas of computer science.