Tag: Equivalent

Introduction

Electrons encounter resistance when they go through a conductor because of the molecules’ attraction forces. The nature of the material determines how much of this resistance is provided. The resistance of the material determines how much electricity flows as a result of voltage differences. Ohm’s law relates electric current (I), voltage (V), and resistance such that,

V = IR

Electrical resistors are devices that provide resistance to an electric circuit. The zigzag symbol in an electrical circuit diagram stands in for a resistor.

System of Resistors

Systems of resistors can be arranged in series or parallel.

1. Resistors in Series Arrangement:

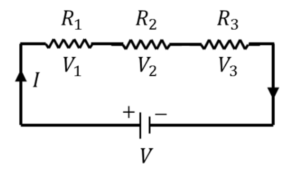
The resistors are arranged in this configuration along the current’s path, one after the other (end to end). As the current passes through the first resistor, its output current enters the second resistor as an input, and the second resistor’s output is then transferred to the third. The equivalent resistor, whose total equivalent resistance is simply the sum of the individual resistance of all the resistors linked in series, may replace all the resistors in a circuit. The equivalent resistor’s formula is:

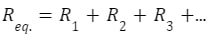
Each resistor in a series circuit receives the same amount of current, and the voltage across each resistor varies proportionally to its resistance.

The total voltage of the circuit is equal to the sum of the voltage across each resistor when the total current, I, in the circuit is multiplied by both sides of the equation.

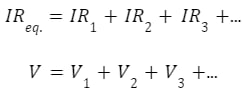
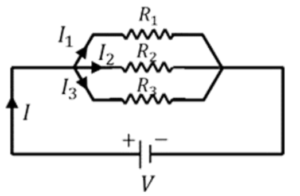
2. Resistors in Parallel Arrangement:

All the parallel resistors in this configuration share an input lead and an output lead, i.e., they are connected across each other. Each resistor in a parallel combination has the same voltage across it, which is the same as the circuit’s overall voltage. At a junction, the electric current is split based on the resistance of each resistor. At the output junction, the whole output current is combined once more and flows through the circuit.

Equivalent resistance in parallel is given as follows:

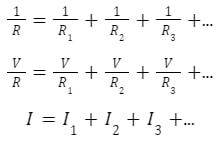
Since the total voltage on each side of the equation is the same, the voltage across each resistor is also the same. We can see that the circuit’s total current, I, equals the sum of the currents flowing through all the resistors.

Summary

Small electrical components known as resistors provide resistance to the passage of electricity in an electric circuit. A circuit can link many resistors in series or parallel configurations. If many resistors are replaced with a single resistor that has the same resistance as the combination, the equivalent resistance of that resistance is the same as the resistance of the series and parallel combination of resistors. The combination formula for series resistors is, Req.=R1 + R2 + R3 +…, and for the parallel combination 1R = 1R1 + 1R2 + 1R3 +…

Frequently Asked Questions

1. What are the Factors on which the Resistance of an Object Depends?

Ans: An object’s electrical resistance is determined by the characteristics of its material and form. The formula takes into consideration these elements:
R= ρ (l/A)
Where A is the cross-sectional area of the material, Rho is its resistivity, and l is the length of the material through which electricity is flowing.

2. What is Electrical Conductivity?

Ans: The inherent capacity of a substance to carry electricity is known as electrical conductivity. It shows how readily electricity can go through the substance. The symbol for conductivity is (sigma), which is just the reciprocal of resistance such that: σ = 1/ ρ
Conductivity equals. Like resistivity, which is a broad attribute of a material that depends on its size. Air is a superb insulator with very low conductivity, whereas metals are typically good conductors with high conductivity and low resistance. Even at temperatures close to absolute zero, superconductors exhibit conductivity.

3. What is the SI unit of Resistivity and Conductivity?

Ans: The most used system of measuring in contemporary times is the SI unit or the International System of Units. The globe uses this contemporary metric system, which is utilised in all languages.
The SI unit of resistivity- ohm metre (Ω.m).
The base SI unit of resistivity- kg.m³.s−³.A-².
The SI unit of conductivity- siemens per metre (S/m).
The base SI unit of conductivity- kg-¹.m-³.s³.A².

Introduction

Ratios are said to be equivalent if they can be made simpler or reduced to the same number. In other words, a ratio is said to be equivalent if it can be expressed as a multiple of another ratio.

A ratio can be expressed using a fraction. The concept of an equivalent ratio is comparable to the concept of equivalent fractions. The antecedent and consequent of a ratio can be multiplied or divided by the same number, other than zero, to create an equivalent ratio.

To get a ratio that is equal to the given ratio, we must first represent the ratio in fraction form. Then, by multiplying or dividing the first term and second term by the same non-zero value, the equivalent fraction can be found. We finally convert it to a ratio.

What are Equivalent Ratios

We must first comprehend what equivalence is to understand the equivalence of ratios. Equivalence is very similar to the well-known mathematical relation equal to, as well as to the same mathematical relationship between different objects. In mathematics, equivalence refers to the concept that two objects are equal but distinct because they have the same overall value. When two ratios share the same simplest form, they are said to be equivalent.

Examples of Equivalent Ratios

We can simply create equivalent ratios by multiplying the antecedent and consequent of a ratio by any real number other than the number zero. Thus, creating some examples of equivalent ratios is a very simple task.

For example, we need to find 5 ratios equivalent to 6:10

We can multiply the given ratio by any real number, let’s multiply it by ½

6: 10 = = 3: 5

Thus 3:5 is a ratio equivalent to 6:10

Other such ratios are, 9:15, 12:20, 15:25, 18:30, etc. these all are ratios equivalent to 6:10.

Methods of Finding Equivalent Ratios

There are two methods to find the equivalence of ratios, these methods are

• Cross Multiplication Method

In this method, we multiply the antecedent of the 1st ratio with the consequent of the 2nd ratio and the antecedent of the 2nd ratio with the consequent of the first. If the two products are equal then we can say that the two ratios are equivalent, otherwise, the ratios are not equivalent.

For example: Let’s say we need to use the cross-multiplication method to determine whether the ratios 3:4 and 6:8 are equivalent.

Therefore, we will multiply each ratio’s antecedent by the other ratio’s consequent.

We can say that the ratios are equivalent if the two products are equal.

In this example: 1st Product

3 × 8 = 24

2nd Product

6 × 4 = 24

Since,

Product 1 = Product 2

The ratios 3:4 and 6:8 are equivalent.

• HCF Method

In this method, we first need to represent the ratios as fractions, then we will reduce that fraction into standard form by finding the HCF of the numerator and the denominator, and then dividing the numerator and denominator by that HCF. After both fractions are reduced to the standard form, if they are equal, then the original fraction, i.e., the ratios were equivalent.

For example: Let’s say that we need to use the HCF method to determine whether the ratios 4:14 and 6:21 are equivalent.

To divide the antecedent and consequent of both ratios with their respective HCFs, we will first check the HCF of the antecedent and consequent for each ratio. If the two ratios are equal after the division, the original ratios were equivalent.

In this example: 1st ratio

4:14

HCF (4, 14) = 2

The ratio in the simplest form,

4: 14 == 2: 7

2nd ratio

6: 21

HCF (6, 21) = 3

The ratio in the simplest form

6: 21 = = 2: 7

Since both ratios in their simplest forms are 2:7, thus the original ratios were equivalent.

Use of Equivalent Ratios

In mathematics and other sciences, equivalent ratios have many applications. Some examples of uses are:

• To make the ratios provided simpler.
• We use equivalent ratios to solve any ratio-related problem.
• To calculate ratios between various fractions.
• Various direct proportionality-related scientific issues.

There are also a lot more uses like this.

Read: Applications of Percentage

Summary

We learned about the circumstances under which ratios or proportions are equivalent in this article. We discussed a few instances of equivalent ratios. The following ideas we learned were how to find equivalent ratios. We also discovered how ratios are equivalent using these techniques. Last but not least, we solved several cases that illustrated the concept of equivalent ratios.

Frequently Asked Questions

1. What are Ratios? What are the Components of Ratios?

Ans: Ratios are defined as a comparison between two quantities of the same type. A ratio has 3 parts, 2 parts are the numbers representing the compared quantities antecedent and consequent, and the third part is a symbol, specifically the ‘:’ (colon) symbol, that is put between the two to represent the comparison.

2. Why are Equivalent Ratios Important?

Ans: The equivalent ratios can be used to explain certain relationships between objects in daily life. For instance, if two pens cost Rs. 10, we can use equivalent ratios to determine the price of any other number of pens or the number of pens that can be purchased with a given sum of money. Many other real-world issues can be resolved using equivalent ratios.

3.What are Proportions? What is the Symbol of Proportions?

Ans: Proportions are a comparison between two or more ratios. If two ratios are in proportion, then they are also equivalent.