Tag: Equation

Introduction

A straight line that intersects another straight line at a 90-degree angle is said to be perpendicular to the first line. The small square in the middle of two perpendicular lines in the figure represents 90 degrees, also known as a right angle. Here, two lines cross at a right angle, indicating that they are perpendicular to one another.

In contrast to sloping or horizontal lines or surfaces, perpendicular lines or surfaces point directly upward. An object is at a 90-degree angle to another if it is perpendicular to it. A pair of lines, vectors, planes, or other objects are said to be perpendicular if they intersect at a right angle. Two vectors are perpendicular if their dot product equals zero.

Perpendiculars

When two lines intersect at a right angle, they are said to be perpendicular to one another. A first line is perpendicular to a second line, more specifically, if the two lines intersect and the straight angle on one side of the first line is split into two congruent angles by the second line at the intersection. Since perpendicularity is symmetric, if one line is perpendicular to another, the other line is also perpendicular to the first. As a result, we don’t need to specify an order when referring to two lines as perpendicular (to one another).

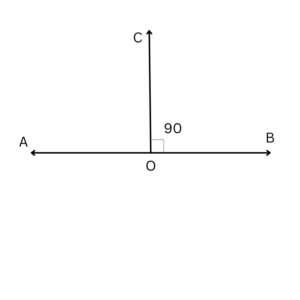
Perpendicular Lines

Segments and rays are easily extended by perpendicularity. If a line segment AB and a line segment CD result in an infinite line when both directions are extended, then the two resulting lines are perpendicular in the sense mentioned above. Line segment AB is perpendicular to line segment CD and can be represented by the symbol AB ⊥ CD. If a line crosses every other line in a plane, it is said to be perpendicular to the plane. The definition of line perpendicularity is necessary for understanding this definition.

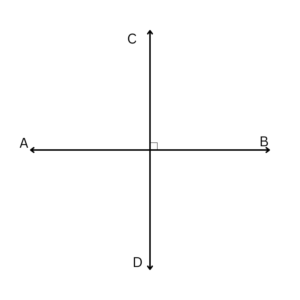
Perpendicular Theorem

According to the perpendicular line theorem, two straight lines are perpendicular to one another if they intersect at a point and create a pair of equal linear angles.

Assume two lines AB and CD intersect each other at O, such that ∠AOC = ∠COB, also since AB is a line, ∠AOC and ∠COB also form a linear pair.

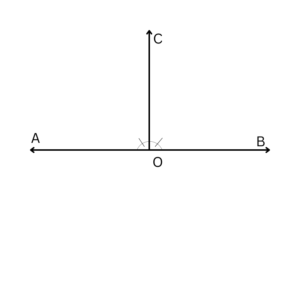
Then, ∠AOC + ∠COB = 180°

Using ∠COB = ∠AOC

⇒ ∠AOC + ∠AOC = 180°

⇒ 2 ∠AOC = 180°

⇒ ∠AOC = 90°

Thus, since the angle of intersection is 90°, we can say that AB is perpendicular to CD and vice versa.

Also Read: Related Angles

Perpendicularity: Slope Formula

Perpendicularity is known as the mathematical condition that two lines need to satisfy to be called perpendicular. Mathematically, if two lines are perpendicular to each other, then the product of their slopes is negative unity.

For example, let two lines of slope . Then these lines are said to be perpendiculars to one another if their slopes have a product -1, i.e.,  

Equation of a Perpendicular Line.

Using the conditions from previous sections, we can find the equation of the perpendicular line to any given line’s equation, at a certain point.

Let, ax + by = c be a line, and we need to find a line perpendicular to it passing through

First, we will find the slope of the given line, 

Slope of a line m = -a/b

Now, using perpendicularity, if the slope of the second line is m’, then for these lines to be perpendicular

m × m’=- 1

⇒ m’ =- 1/m =- 1/-a/b = b/a

Thus, the slope of the perpendicular line is, 

m’= b/a

Then, we have a point as well as the slope for the equation of the perpendicular line,

Using point-slope form

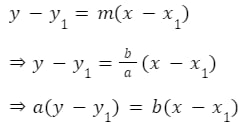
If we know the exact values of a, b and then we can further simplify this equation.

Interesting Facts about Perpendicular Lines

• In order to obtain the maximum support for the roof, walls and pillars are constructed perpendicular to the ground in our homes and other buildings. This is just one example of how perpendiculars are used in everyday life.
• Perpendiculars of two lines that meet at an angle will also meet at that same angle.

Solved Examples

Example: Which of the following pair of lines are perpendicular, parallel, or simply intersecting?

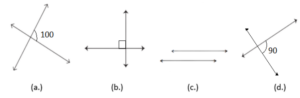
1. Intersecting, since the angle of intersection here is given to be 100 degrees.
2. Perpendicular, as we know the right angle is also represented by a small square, we can say that these lines are perpendicular to each other.
3. Parallel lines, clearly extending these lines to infinity we will never see them intersecting; thus, they are parallel.
4. Perpendicular, clearly the angle of intersection here is given to be 90 degrees.

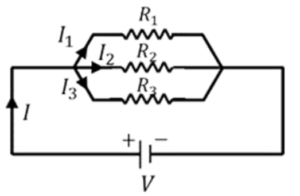
Summary

The subject of perpendiculars and the perpendicularity of lines were covered in this article. The reader should be able to comprehend the meaning of perpendicular lines, the symbol used to represent them, as well as the formula and theorems relating to perpendicular lines, after carefully reading this article. Two lines are said to be perpendicular if their angle of intersection is a right angle. The slopes of perpendicular lines are negative reciprocals of each other.

Frequently Asked Questions (FAQs)

1.What are Perpendicular Lines?

Ans. When two lines intersect at an angle of 90 degrees, the lines are said to be perpendicular to each other.

2. How do you Find the Slope of a line Perpendicular to a Given Line?

Ans. The slope of perpendicular lines are negative reciprocals of each other; thus, the slope of a perpendicular line can be found simply by negating the reciprocal of the slope of the given line.

3. What are Perpendicular Bisectors?

Ans. A line that divides another line segment into two halves while also being at a right angle to it is known as the perpendicular bisector of the line segment.

4. Are all Intersecting Lines Perpendicular?

Ans. No, all intersecting lines are not perpendicular, but all perpendicular lines are intersecting, that too at a specific angle, i.e., 90 degree.

Also read: Properties, Area of Right-Angled Triangles

Introduction

Electrons encounter resistance when they go through a conductor because of the molecules’ attraction forces. The nature of the material determines how much of this resistance is provided. The resistance of the material determines how much electricity flows as a result of voltage differences. Ohm’s law relates electric current (I), voltage (V), and resistance such that,

V = IR

Electrical resistors are devices that provide resistance to an electric circuit. The zigzag symbol in an electrical circuit diagram stands in for a resistor.

System of Resistors

Systems of resistors can be arranged in series or parallel.

1. Resistors in Series Arrangement:

The resistors are arranged in this configuration along the current’s path, one after the other (end to end). As the current passes through the first resistor, its output current enters the second resistor as an input, and the second resistor’s output is then transferred to the third. The equivalent resistor, whose total equivalent resistance is simply the sum of the individual resistance of all the resistors linked in series, may replace all the resistors in a circuit. The equivalent resistor’s formula is:

Each resistor in a series circuit receives the same amount of current, and the voltage across each resistor varies proportionally to its resistance.

The total voltage of the circuit is equal to the sum of the voltage across each resistor when the total current, I, in the circuit is multiplied by both sides of the equation.

2. Resistors in Parallel Arrangement:

All the parallel resistors in this configuration share an input lead and an output lead, i.e., they are connected across each other. Each resistor in a parallel combination has the same voltage across it, which is the same as the circuit’s overall voltage. At a junction, the electric current is split based on the resistance of each resistor. At the output junction, the whole output current is combined once more and flows through the circuit.

Equivalent resistance in parallel is given as follows:

Since the total voltage on each side of the equation is the same, the voltage across each resistor is also the same. We can see that the circuit’s total current, I, equals the sum of the currents flowing through all the resistors.

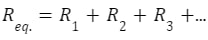
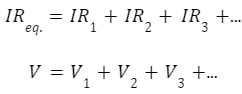
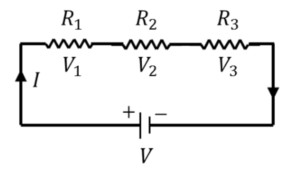
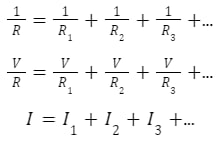
Summary

Small electrical components known as resistors provide resistance to the passage of electricity in an electric circuit. A circuit can link many resistors in series or parallel configurations. If many resistors are replaced with a single resistor that has the same resistance as the combination, the equivalent resistance of that resistance is the same as the resistance of the series and parallel combination of resistors. The combination formula for series resistors is, Req.=R1 + R2 + R3 +…, and for the parallel combination 1R = 1R1 + 1R2 + 1R3 +…

Frequently Asked Questions

1. What are the Factors on which the Resistance of an Object Depends?

Ans: An object’s electrical resistance is determined by the characteristics of its material and form. The formula takes into consideration these elements:
R= ρ (l/A)
Where A is the cross-sectional area of the material, Rho is its resistivity, and l is the length of the material through which electricity is flowing.

2. What is Electrical Conductivity?

Ans: The inherent capacity of a substance to carry electricity is known as electrical conductivity. It shows how readily electricity can go through the substance. The symbol for conductivity is (sigma), which is just the reciprocal of resistance such that: σ = 1/ ρ
Conductivity equals. Like resistivity, which is a broad attribute of a material that depends on its size. Air is a superb insulator with very low conductivity, whereas metals are typically good conductors with high conductivity and low resistance. Even at temperatures close to absolute zero, superconductors exhibit conductivity.

3. What is the SI unit of Resistivity and Conductivity?

Ans: The most used system of measuring in contemporary times is the SI unit or the International System of Units. The globe uses this contemporary metric system, which is utilised in all languages.
The SI unit of resistivity- ohm metre (Ω.m).
The base SI unit of resistivity- kg.m³.s−³.A-².
The SI unit of conductivity- siemens per metre (S/m).
The base SI unit of conductivity- kg-¹.m-³.s³.A².