Introduction
In scientific measurements, it is impossible to achieve perfection and obtain error-free results. Every experiment will have some degree of error, which may vary with each repetition. For instance, the commonly accepted value for Earth’s acceleration due to gravity is 9.80665 \(m/{s^2}\), but if you were to measure it experimentally, you would get a different result. Due to this, it is necessary to have methods to describe errors in measurements. Two important terms that help us evaluate measurement errors are accuracy and precision, and they will be discussed in depth in this article.
Define Accuracy
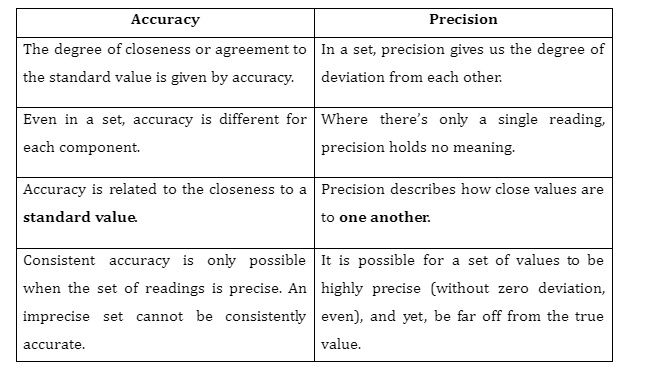
There always exists a true value of the quantity being measured. For instance, the true value of the refractive index of water is 1.33333. The accuracy of a measurement refers to how close it is to the true value. If a measurement of the refractive index of water gives you the value 1.31, you would consider it to have good accuracy because it is close to the true value. An important thing to note is that accuracy is evaluated on a per-reading basis, and even within a set of readings, each reading may have different accuracy. The overall accuracy of the set can be determined by checking if its mean is close to the true value.
What is Precision?
It is always a good practice to take multiple readings while performing a measurement. This helps minimize errors. For a set of readings to be considered precise, the readings in the set must not deviate too much from each other. For instance, suppose you arrived at the following values while measuring the length of a stick:
- 1.01 m
- 1.02 m
- 0.99 m
- 1.02 m
As is evident, all of these readings are significantly close to each other, making this a precise set. Contrary to accuracy, precision is defined for the whole set, not just one reading.

Accuracy and precision
Accuracy and Precision Examples
The following examples will make the concept clearer:
Example 1: Five friends record the height of their 1.76m tall classmate as follows:
- 1.74 m
- 1.78 m
- 1.73 m
- 1.72 m
- 1.75 m.
This set is a very precise set since all readings lie close to each other. Within the set, the last measurement is highly accurate since it only deviates 0.01m from the true value. On the other hand, the fourth friend is off by 0.04m and is the least accurate person in the group.
Example 2: This time, let the height measured by the girl’s classmates be:
- 1.51 m
- 1.61 m
- 1.88 m
- 1.72 m
- 1.80 m
This set demonstrates low precision since the values are spread so far apart we can’t even decipher what the true value could possibly be.
Distinguish between Accuracy and Precision
What is False Precision?
False precision can be present in data that appears to be more precise than it actually is. This causes the data to be misleading.
This can occur when converting between units, such as when the speed of a car travelling at 40 mph is expressed as 64.3738 km/h, with four significant digits after the decimal point, despite the original measurement having none. Other instances where false precision may appear include:
-
False precision can arise when unnecessary zeros are added to measurements. For instance, 1 m and 1.00 m are equivalent mathematically, but including the extra zeros in 1.00 m implies a level of precision that may not be achievable by our instrument. This leads to a false sense of precision.
-
Combination of data that carries varying levels of precision can lead to false precision.

False precision
Quantification of Data
The process of expressing a value in numerical terms is known as “quantification”. This is crucial in science as it gives a more defined and specific description of a phenomenon. For instance, calling a burger large has no scientific meaning. Instead, we must specify the weight of the burger for it to make mathematical sense.
Quantification is necessary as computers only understand numerical data, which is a requirement for computer-based analysis. Furthermore, quantification enables us to conduct statistical analysis, which is useful in fields such as machine learning and artificial intelligence.
Practice Questions
Q1. Given that the refractive index of water is 1.3333, discuss whether the following set is accurate and/or precise.
- 1.32
- 1.54
- 1.11
- 1.61
- 1.22
Ans. We consider a set like this to be imprecise since the readings vary significantly. At the same time, the value 1.32 is highly accurate, while 1.61 is a very wrong result.
Q2. To measure the length of his pencil, a student uses a metre-scale and writes the result as 0.1237 m. He is given a zero for this measurement. Justify.
Ans. A metre scale does not have the precision the student provided here. It can only measure up to 1 mm, while the student measured it up to one-tenth of a millimetre. This is false precision.
Q3. What makes the following set a bad set of readings for the acceleration due to gravity?
- 9.805 \(m/{s^2}\)
- 9.005 \(m/{s^2}\)
- 10.610 \(m/{s^2}\)
- 10.100\(m/{s^2}\)
- 9.512 \(m/{s^2}\)
Ans. If we take the average of these readings, it comes out to be only 0.002% away from the standard or accepted value. One might call that accurate, but these readings vary too much from each other and thus, this set is imprecise.
Summary
Measuring without any form of error is impossible, making it crucial for us to understand and quantify errors in scientific experiments. Accuracy and precision are two key elements in analysing such errors. Accuracy refers to the deviation of a measurement from its true or accepted value and is unique to each individual measurement. Precision, on the other hand, reflects the consistency of measurements within a set, and is not defined for a single measurement. A combination of high accuracy and precision results in reliable data, while a lack of either makes a reading or set of reading bad. False precision occurs when data appears more precise than it actually is, often through presentation or the mixing of data with varying precision.
Quantification, or converting data into numerical form, is an important process since it is necessary for computer analysis, machine learning, and artificial intelligence.
Frequently Asked Questions
1. How do you find the percentage error from a known value?
We can calculate percentage error with the following formula:
\({\bf{e}} = \frac{{{\bf{experimental}}{\rm{ }}{\bf{value}} – {\bf{true}}{\rm{ }}{\bf{value}}}}{{{\bf{true}}{\rm{ }}{\bf{value}}}} \times {\bf{100}}{\rm{ }}\% \)
2. How many significant digits should we use while performing calculations?
In theoretical calculations, we use as many significant digits as are provided to us initially. While performing experiments, the number of our significant digits is determined by the limitations of our instruments.
3. Of accuracy and precision, which is more important?
For scientific data to be considered good, it must be both precise and accurate.
4. Discuss accuracy and precision in terms of statistical analysis.
Statistically, a data set is accurate if its mean is close to the accepted or true value. And for the data to be precise, its standard deviation must be small.
5. How do we decide if our data is accurate enough?
As a general guideline, you can determine the error margin allowed by dividing the place value of the least significant digit by 2.
For instance, if the true value is stated as 43.71 m, the place value of the least significant digit (1) is 0.01 m. Hence, if your measurement is within ±0.005 m of the true value, it can be considered accurate.