Introduction
The most fundamental application of percentages is to compare two amounts while setting the second amount to 100. The use of percentages is widespread and varied aside from this. For instance, a lot of statistics in the media are expressed as percentages, including bank interest rates, retail discounts, and inflation rates. Percentages are essential for understanding the financial aspects of daily life.
The Latin word “per centum,” which means “per hundred,” is where the word “percent” originates. The task of comparing unlike fractions is very challenging. Because percentages are the numerators of fractions with a denominator of 100. Percentages have a wide range of applications in daily life, including making simple comparisons, allocating discounts in marketing, and calculating profits and losses for businesses.
Percentages
Per means “out of” in percentage, and cent means a century. In essence, the whole is always set to 100, and the relationship is between a part and the entire. The ratio known as a percentage has a denominator of 100 and the percentage symbol %.
The percentage formula is as follows:

How to find percentage from data?
To find percentage from a given data, we first need to find the fraction of the quantity from the given data. By dividing the number by a whole and multiplying the result by 100, any fraction can be expressed in percentages. Consider a society with 1000 members, 650 of whom are voters. Then the percentage of voters out of all the residents is,
% Of voters = ![]() × 100
× 100
= ![]() × 100
× 100
= 65%
Percentage of a Number
When a number is divided into 100 equal parts, the percentage of that number is the sum of those 100 parts. Calculating percentages involves multiplying the total number by the percent expressed as a fraction. For instance, let’s say we need to find 30% of 600. We can figure it out as:
30% of 600 = 600 × ![]() = 180
= 180
Here, 600 is total, so 30% of 600 is 180.
Applications of Percentages
One of the most useful mathematical ideas is the percentage, which has applications in practically every branch of science as well as in everyday life.
To compare fractions
Fractions can be converted to percentages to create a clear comparison representation. This is very useful when the denominators of two fractions have different values. For instance, suppose you need to compare the fractions 2/5 and 1/4. We use percentages because making a direct comparison in this situation is very difficult. For 2/5, the percentage form is 40%, and for 1/4, the percentage form is 25%. We can categorically state that 2/5 is greater than 1/4.
To estimate increment or decrement
Any change in a quantity can be expressed in terms of a percentage. For instance, a 20% decrease would occur if a person’s salary was Rs. 5000 per month one year and Rs. 4000 the following.
The formula to calculate % change in a quantity is
Change% = ![]() × 100
× 100
To calculate ‘How much’ or ‘How many’
Sometimes numbers are expressed as percentages, for example the case of a city where 40% of the people are vegan. Therefore, the percentage will enable us to determine the precise number of vegans.
The formula to calculate the number from percentage is as follows,
Quantity = ![]() × Total
× Total
To calculate profit or loss in percentage, to mark discounts etc.
If the selling price and cost price are known, the seller can use percentages to determine its loss or profit. For instance, a seller may charge Rs. 5000 for a fan while only paying Rs. 4000. The profit margin in this case is 25%.
Solved Examples
Example: What is the discount given on an article marked Rs. 6000 with a discount of 30%.
Solution: The discount on the article is given by
Discount% = ![]() × 100
× 100
Discount = ![]() × Marked Price
× Marked Price
Substituting values
Discount = ![]() × 6000 = Rs. 1800
× 6000 = Rs. 1800
A discount of Rs. 1800 is given.
Example: By what percentage is Amit’s salary, Rs. 35000, is less than from Sagar’s salary, Rs. 40000?
Solution: The difference between Amit’s and Sagar’s Salaries is
Sagar’s Salary – Amit’s Salary = 40000 – 35000 = Rs. 5000
The percentage difference between their salaries
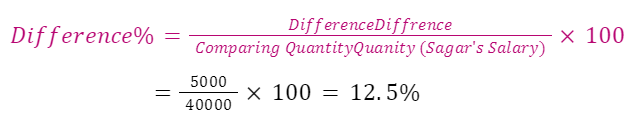
Thus, Amit’s salary is 12.5% less than Sagar’s salary.
Summary
When portions of a quantity are given, we have seen how to convert ratios into percentages. We discussed the formula for calculating the percentage of a number. An increase or decrease in a specified quantity can also be expressed as a percentage. The profit or loss in a specific transaction can be expressed in terms of percentages.
Frequently Asked Questions
1.What is the Importance of Percentage in Sciences other than Mathematics?
Ans. Percentage plays an important role in many aspects of business science, physical science, chemical science etc. In business science (statistics in particular) percentage is used to represent the parts of a data. In physical science percentage is used in various formulae, and derivations to represent efficiency, error and other such things. In chemical science percentage is used to calculate the concentration of different chemicals and composition of solutions etc.
2.How is Percentile Different from Percentage?
Ans. The value in the distribution or level at or below which a specific percentage of the score lies is represented by the percentile. For every hundred, which is the measurement unit, is referred to as the percentage.
3.What is the Relationship between Percentage and Probability?
Ans. Probability of an event can also be expressed as a percentage. For example, if the probability of an event is x, then the percentage probability is given by
% Probability = 𝑥 x 100%
Read More: Ratio and Percentage Formula and Examples