Tag: Dimension

Introduction

If all three angles and three sides of one triangle are the same size and dimension as the corresponding angles and sides of the other triangle, then the two triangles are said to be congruent.

The size and shape of any two congruent triangles are the same. Angles in one triangle have a measure that is the same as angles in another triangle. The corresponding sides of the congruent triangles also have equal lengths. Triangles that are congruent with one another can reflect or rotate another.

Congruent Meaning

If two figures can be placed exactly over one another, they are said to be “congruent.”

Take bread example as an example. The bread slices are stacked one on top of the other so that the top slice completely encloses the bottom slice. When stacked on top of the other, every slice of bread is the same size and shape. When something is congruent, it must have the same size and shape. Mathematics uses the term “congruence” to describe when two figures have similar sizes and shapes.

Congruence of Triangles

A triangle is a closed 3-sided figure in geometry. A triangle is a closed polygon made up of three lines that intersect at three different angles. The two triangles are said to be congruent if all three corresponding sides are equal and all three corresponding angles have the same measure. The appearance of these triangles remains constant when they are moved, rotated, flipped, or turned. If the triangles are moved, they must be superimposed to be congruent. As a result, if the triangles’ corresponding sides and angles are equal, the triangles are congruent. Thus, along the corresponding sides and angles, the congruent triangles can be stacked one on top of the other.

Online Coaching Maths Tuition Classes 7 Are The Best Way To Go

Congruence Criteria for Triangles

Five triangle congruence rules can be used to determine whether a given pair of triangles are congruent or not. The six dimensions allow for a perfect definition of any triangle. The particular triangle has three sides, as well as three angles. As a result, only three of the triangles’ six parts can be used to determine whether two triangles are congruent. The acronym CPCT stands for “Corresponding parts of Congruent triangles”. Triangles can be shown to be congruent, at which point the remaining dimension can be predicted without having to calculate the triangles’ missing sides and angles. The following lists the five triangle congruence rules.

• SSS (Side-Side-Side)
• SAS (Side-Angle-Side)
• ASA (Angle-Side-Angle)
• AAS (Angle-Angle-Side)
• RHS (Right angle -Hypotenuse-Side)

Note: ASA and AAS are not the same. Like ASA and AAS, SAS does not have any related counterpart like SSA, However, a variation of ASS exists for right triangles as RHS, where R is the angle and the other two, i.e., H and S, are sides.

Congruent Triangles Properties – CPCT

Congruent triangles have all their sides and angle equal, thus if two triangles are where we know all the properties of one and not the other, then we can find all the properties of the second triangle by simply comparing the corresponding parts in the first. Congruent triangles are most frequently referred to using the abbreviation CPCT. The term “Corresponding Parts of Congruent Triangles” is abbreviated as CPCT. It is a crucial characteristic of congruent triangles. Congruent triangles’ respective parts are always equal. The congruent triangle properties refer to this.

Types of Congruence

There are 5 types of triangle congruence criteria.

Side Side Side (SSS)

Side Side Side or also known as SSS congruence criteria states that if all three sides of two triangles are equal, then the triangles are congruent.

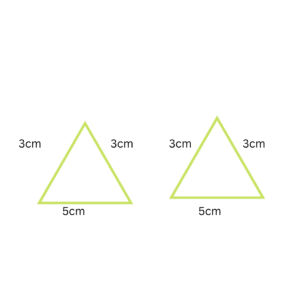
Side Angle Side (SAS)

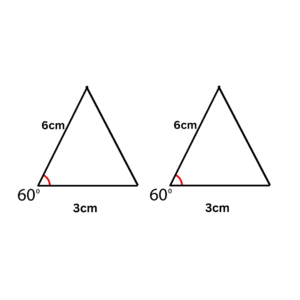
Side Angle Side or also known as SAS congruence criteria states that if two sides and their included angles are equal in two triangles, then the triangles are congruent.

Angle Side Angle (ASA)

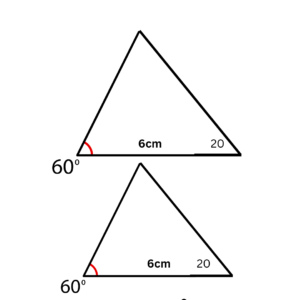
Angle Side Angle or also known as ASA congruence criteria states that if a side and two angles on it are equal in two triangles, then the triangles are congruent.

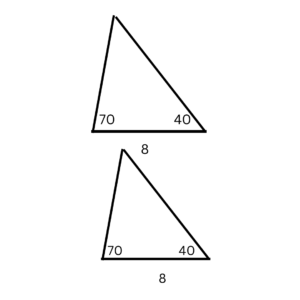
Angle Angle Side (AAS)

Angle Angle Side or also known as AAS congruence criteria states that if two angles and a side not common to the two angles are equal in two triangles, then the triangles are congruent.

Right angle Hypotenuse Side (RHS)

Right angle Hypotenuse Side or RHS congruence criteria only applies to right triangles, it says that in two triangles if they have a right angle, and their hypotenuses and one other side are equal in both triangles, then the triangles are congruent.

Summary

In this article, the topic of congruence is discussed in detail. If two figures share the same shape and size, they are said to be congruent; alternatively, if a figure shares the same shape and size as its mirror image, it is said to be congruent to its mirror image.

This article also shines a light on the topic of Rules of congruence for triangles. There are 5 basic congruence criteria, namely SSS, SAS, ASA, AAS, and RHS.

For more help, you can Refer to Lesson 23 congruence of Triangles in Math Class 7.

Frequently Asked Questions

1. What do you mean by Congruence?

Ans 1. Congruent figures are geometric objects that share the same size and shape in mathematics. The two figures are equal and are referred to as congruent figures.

2. Are all Squares Congruent?

Ans 2. No, all squares are not congruent, since for congruence two figures must have all of their quantifying dimensions must be equal, that includes all the sides and all the angles. All squares have the same angles, but their side lengths are different, hence they aren’t congruent.

3. Is AAA a criterion for the Congruence of Triangles?

Ans 3. No, AAA is not a criterion for congruence because even if all the angles of two triangles are equal, that necessarily does not mean that they have the same side length, for example two equilateral triangles of sides 3cm and 5cm, both have the same 60-60-60 angle, but they are not congruent because their sides are of different lengths.

Introduction

One type of energy that is essential to our existence is light. We are unable to envision a world without light. Light improves the beauty of everything around us and allows us to see. In both science and art, light is a crucial element. One of the crucial scientific instruments that enable scientists to examine things all across the world is light.

Some scientific theories claim that it is made up of particles, while others assert that it is made up of waves. What is the medium of propagation if the light is a wave? How does light move? We shall find answers to some of these questions in this article.

How does Light Travel?

Light can pass through a medium and in a vacuum. However, there won’t be any particles in a vacuum that light can’t reflect off of. Therefore, light is invisible in a vacuum. Light can reflect in the air when it strikes dust or other particles, making light visible in the atmosphere. Light may be thought of as having waves. Different light waves have varied wavelengths, and different light has different colours based on the wavelength. For instance, the shortest wavelength of light has a violet colour, whereas the highest wavelength of visible light has a red colour. Light, being a wave, may exhibit wave characteristics like diffraction and interference.

The answer to the question of how light typically moves is that it moves straightforwardly. However, the truth is that light’s smaller diffraction effect is the reason it appears to move in a straight line. The spreading out and the illumination of an area where a shadow is anticipated is known as diffraction, which is the bending of waves around an object. The wavelength of light is on the order of nanometers. We cannot see impediments of this size with our unaided eyes because the wavelength is too narrow. As a result, we see that light moves in a straight path. Rectilinear propagation of light is another name for the way that light moves in a straight line.

Want to get an “A” on your Science exams? Let our expert teachers be your guide toward improving your grades and reaching your highest potential. Study Science tuition for classes 6th, 7th, and 8th.

Experiment with the Straight Line Motion of Light

Normal light travels in a straight line because there isn’t enough diffraction to cause any noticeable effects. We demonstrate that light moves in a straight line using a basic experimental setup. In front of a candle on the tabletop, arrange three cardboard sheets back to back. Ensure that the candles and cardboard sheets are arranged in a straight line. On each cardboard sheet, poke a pinhole after lighting the candle. To allow for the visibility of the candle’s flame, the holes must be made at equal heights. Now, observe which line light travels in by looking through the holes. Along the slender line of holes, the thin flame will be visible. Now move one of the cardboard sheets to either side and observe the flame. Can you see the flame? The flame won’t be seen when you move the cardboard sheet. Reposition the cardboard sheet in its original location. The flame may now be seen. The experiment diagram is shown below. From this experiment, we may infer that light moves in a straight line.

Examples of Straight-Line Motion of Light

• When a lamp, torch, or another source of light emits light, it travels in a straight line.
• When sunlight enters a dusty environment through tiny holes, a straight-line trail of light is apparent.
• The object will become invisible when an opaque object is placed in front of it. The reason for this is that an opaque object prevents light from bending through its corners.

Summary

The light rays move in a straight line. The minimized diffraction effects of light facilitate the propagation of the light in a straight path. Examples, where the light rays travel in a straight line, are the light ray that comes from a train, a torch, and/or a lamp.

Frequently Asked Questions

1. What is Rectilinear Propagation of Light?

Ans: The motion of the light rays in a straight line is termed the rectilinear propagation of the light.

2. Explain why Light Travels in a Straight Line?

Ans: Diffraction is a wave characteristic of light. Only when the wavelength of the light wave is of the order of the dimension of the size of the particle it collides with, and the phenomena of diffraction take place. The wavelengths of light are on the order of nanometers. Typically, a nanometer-sized item is invisible to the human eye. Light’s diffraction impact is therefore too modest to be taken into account and travels in a straight-line path.

3. Why is Light Invisible in a Vacuum?

Ans: Light can travel through the vacuum, however, since there are no particles available in the vacuum, light cannot reflect in a vacuum and therefore light is invisible in a vacuum.