Tag: Cube

Introduction

There are many geometrical solids around us. For example, two kids are playing board games using dice & coins. One boy is trying to solve Rubik’s cube. One thing that is common in the above examples is that these objects are in the shape of cubes. In this tutorial, we are going to discuss the topic of cubes & volume of a cube. A cube is a three-dimensional solid object having equal sides & faces. A cube has six faces, twelve edges & vertices. It is also known as the regular hexahedron or square prism. Volume of a cube is the amount of space occupied by the cube. It is one of the essential & fundamental concepts in geometry. The concept of the volume of a cube is majorly used for finding the capacity of a cubical tank.

What is a cube?

A cube is a symmetrical three-dimensional solid object bounded by six faces, facets or sides with three meeting at the point or corner known as the vertex. The cube has six faces, twelve edges & eight vertices. The dimensions of a cube are the same. It is also known as the regular hexahedron or square prism. Cube is a platonic solid (solid having congruent faces.)

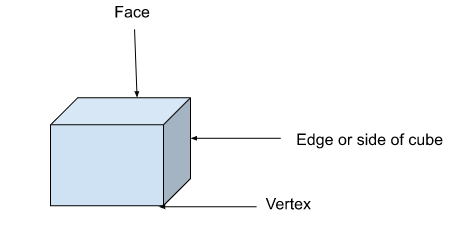
The above figure represents a cube. Dice, ice cubes & Rubik’s cubes are some real-life examples of cubes. 

Some properties of the cube :

• A cube has 12 edges, 6 faces & 8 vertices. Faces of the cubes are square, therefore length, breadth & height of the cubes are equal.
• The angles between any edges & faces are \({90^0}\).
• The opposite planes or faces are parallel to each other.
• Three edges & three planes meet at each vertex of the cube.

What is volume of cube ?

The volume of a cube is a three-dimensional space occupied by the cube. For computing, the volume of the cube has two different formulas depending upon different parameters. By knowing the length of an edge of the cube we can calculate the volume of a cube. Also, the volume of a cube can be calculated by using a length of a diagonal. the volume of a cube is expressed in cubic units. Most of the time volume of cubes is expressed in SI units  \({m^3}\) in CGS units, \({cm^3}\) & litre.

Volume of a cube can be calculated by using two methods :

1) By using edge length 

2) By using diagonal

1) By using edge length

The volume of a cube having edge length ‘l’ can be calculated as 

Volume of a cube = length x breadth x height

 \(\begin{array}{l} = l \times l \times l\\ = {a^3}\end{array}\)

Derivation for a volume of a cube:

Consider a square sheet. The area of a sheet will be taken as surface area, the area of a sheet is length x breadth.

As the sheet is square. It has equal length & breadth, therefore the surface area will be \({a^2}\).

By stacking multiple sheets on top of each other square can be formed so that we will get height ‘a’ of a cube. 

Now, we can conclude as the overall area covered by the cube will be the area of the base multiplied by the height.

So, the volume of a cube \( = {a^2} \times a = {a^3}\)

So here we can conclude as the Volume of the cube \( = {\left( {side} \right)^3} \)

For example, the Volume of a cube having a side of 3 m can be calculated as  

             \( = {\left( {side} \right)^3} = {\left( 3 \right)^3} = 27{m^3}\)

2) By using diagonal 

Volume of a cube can be calculated by using a formula,

Volume of a cube \( = \frac{{\sqrt 3  \times {d^3}}}{9}\)

Here d is the diagonal of the cube 

For example, Length of a diagonal is 3 cm, then the volume of the cube will be

\[ = \frac{{\sqrt 3  \times {d^3}}}{9} = \frac{{\sqrt 3  \times {{\left( 3 \right)}^3}}}{9} = 3\sqrt 3 c{m^3}\]

Some other important formulae of a cube:

i)Total surface area of the cube =\(6{l^2}\) units

ii)Lateral surface area of the cube =\(4{l^2}\) units

Also Read: how to calculate volume of cuboid
                  how to find the volume of a sphere

Solved examples:

Q 1) Calculate the volume of a cube if the edge length of a cube is 

i) 9 cm

ii) 5.2 cm

 iii) 7.5 cm

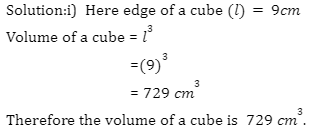
   ii) 5.2 cm

 iii) 7.5 cm

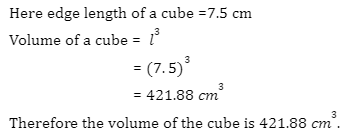
Q 2) Calculate the edge length of a cube if the volume of the cube is

Q 3) Compute the volume of a cube which has a total surface area of 661.5 sq. cm.

Solution: Here, the total surface area = 661.5 sq. cm and the volume of a cube =?

Using the formula for the total surface area of a cube,

Q 4) Calculate the volume of the cube having a diagonal of 5 units.

Solution: Here length of a diagonal = 5 units 

Volume of a cube by a diagonal formula is given as,

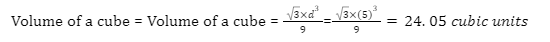
Therefore, the volume of the cube is 24.05 cubic units

Word problems :

1) A cubical tank can store 1331000 ml of water. Then compute the side of the tank in cm.

Solution: Volume of a tank = 1331000 ml

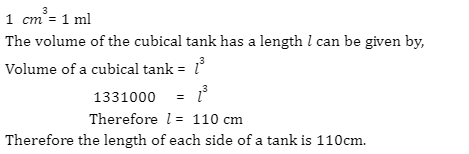
2) Calculate the number of cubes when we cut a cube with an edge of 27 cm into cubes having an edge length of 3 cm?

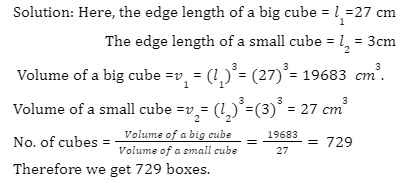
Summary :

In this tutorial, we have learned about cubes & how to calculate the volume of cubes. A cube is a three-dimensional solid object having equal faces & edge lengths. Volume of a cube is a space occupied by a cube. Rubik’s cube, cubical tank, cubical box, and dice are some real-life examples of cubes. The volume of a cube can be calculated by two methods. The first is by using the edge length formula & by using the diagonal formula. This concept has wide application in real life. The concept of the volume of a cube is mainly used to determine the capacity of a cubical tank & find the side of a tank. This tutorial will surely help you to understand cubes & volume of cubes.

 

Frequently Asked Questions 

1. Why cube is known as a regular hexahedron?

Ans. A regular hexahedron is a 3D solid object having six congruent faces. Cube has six congruent faces, therefore cube is known as the regular hexahedron.

2. State the difference between cube & cuboid?

Ans. A cube is a three-dimensional solid object having all square faces whereas a cuboid is a three-dimensional object having all rectangle faces.

3. Can a prism be a cube?

Ans. A cube is a prism because a cube is considered one of the platonic solids.

4. State the difference between the surface area & lateral surface area of a cube?

Ans. For the calculating surface area of a cube sum of the area of all faces is taken whereas for calculating lateral surface area sum of only four surfaces is taken.

i)Total surface area of the cube = \(6{l^2}\) units

ii)Lateral surface area of the cube =  \(4{l^2}\) units

5. Explain what is net of a cube is?

Ans. The net of a cube is formed when the square faces of the cube are flattened by separating at the edges to form a 2D figure. Through that figure, we can see six faces of the cube.

Join our 8th class online Math Tuition to learn all about the Volume of a Cube! Our experienced tutors will provide you with a comprehensive understanding of this fundamental concept, and help you to excel in your exams.

Introduction

When a number (n) is multiplied three times, the result is known as the cube of that number. As a result, the cube of the number (n) is \({n^3}\) or n-cubed. Select the number 4 as an example. We already know that . As a result, 64 is known as the cube of 4. The cube root of a number, on the other hand, is the inverse of the cube of a number and is denoted by \(\sqrt[3]{{}}\) In the same example, 4 is called the cube root of 64. Let’s go ahead and learn more about the numbers’ cubes and cube roots.

What is a cube of a number?

A cube number is an outcome of multiplying an integer by the same integer three times. They also go by the name “perfect cubes,” or cube numbers. For example, \(4 \times 4 \times 4 = {4^3} = 64\). A  number multiplied by the same number three times is called a cube number, or a number with the exponential power of three. Because a negative number produces a negative number when it is multiplied by the same negative number three times, cube numbers of positive numbers are positive, while cube numbers of negative numbers are negative. For example, \({\left( { – 6} \right)^3}\)

In geometry, a cube’s volume is equal to the product of its length, breadth, and height. The length, breadth, and height are all equal inside the cube because it is a cube. The cube’s volume is therefore equal to , which  is its length, height, and width. This implies that a cube’s volume is a cube number.

What are the cube roots?

When we hear the word cube root, the first two words that come to mind are cube and roots. In this sense, the concepts are somewhat similar; “root” refers to the primary source of origin. As a result, we only need to consider “which number’s cube must be chosen to get the given number.”

In a nutshell, the cube root of any number is the factor that is multiplied three times to obtain the specific values. Keep in mind that a number’s cube root is the inverse of the number’s cube.

Cube roots by prime factorization

The prime factorization method can be used to calculate the cube root of a number. Begin by determining the prime factorization of a given number to find its cube root. Then, divide the obtained factors into groups, each having three identical factors. Then, to get the answer, eliminate the symbol of the cube root and multiply the factors. If any factor remains that cannot be equally divided into sets of three, the given number isn’t a perfect cube, and we cannot determine its cube root. 

Example: How to determine the cube root of 10648.

 

\(\begin{array}{l}\sqrt[3]{{10648}} = \sqrt[3]{{2 \times 2 \times 2 \times 11 \times  \times 11 \times  \times 11}}\\\;\;\;\;\;\;\;\;\;\;\; = 2 \times 11 = 22\end{array}\) 

Cube roots by estimation

If a number has several digits, it will be difficult for you to use the prime factorization and long division methods to compute the square and cube roots of the number. You will thus attempt to estimate the cube root and square root values for these numbers. Factorization becomes challenging as the number of digits rises. Estimating a square root and a cube root in such circumstances is a wise move.

The following step can be used to determine a large integer’s cube root using the estimation method if it is claimed that the provided number is a perfect cube.

Step 1: Starting with the rightmost digit, create a group of three digits starting with any cube number, such as 19683, whose cube root needs to be found.

Step 2: The unit’s digit of the necessary cube root will be provided by the first group. Since the unit digit is 3, we need to find the cube root of the cube which also has unit digit 3, i.e., \({7^3} = 343\) has unit digit 3. Hence, our unit digit for the cube root is 7.

Step 3: Now take the second group, i.e., 19, and find the cube root that is just smaller than 19 ( second group ).

\({2^3} < 19 < {3^3}\).

8 or  is just smaller than 19 hence our tenths place digit is 2.

Hence, the cube root of 19683 is equal to

\(\sqrt {19683}  = 27\)

Solved examples

Example 1: Determine the following:

1. \(\sqrt[3]{{729}}\)

Solution: We will be using the prime factorization method.

From it, we will get

Now operate both the sides under the cube root.

\(\begin{array}{l}\sqrt[3]{{729}} = \sqrt[3]{{3 \times 3 \times 3 \times 3 \times 3 \times 3}}\\\;\sqrt[3]{{729}} = 3 \times 3 = 9\end{array}\)

2. \(\sqrt[3]{{1728}}\)

Solution: We will be using the prime factorization method.

From it, we will get

Now operate both the sides under the cube root.

\(\begin{array}{l}\sqrt[3]{{1728}} = \sqrt[3]{{2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 3 \times 3 \times 3}}\\\;\sqrt[3]{{1728}} = 2 \times 2 \times 3 = 12\end{array}\)

3. \(\sqrt[3]{{2744}}\)

Solution: We will be using the prime factorization method.

From it, we will get

Now operate both the sides under the cube root.

\(\begin{array}{l}\sqrt[3]{{2744}} = \sqrt[3]{{2 \times 2 \times 2 \times 7 \times 7 \times 7}}\\\;\sqrt[3]{{2744}}\; = 2 \times 7 = 14\end{array}\)

Example 2: Determine the cube root of 59319 using estimation.

Solution:

The given number is 59319

First, we have to make the group of three from the right side. So we have the first group (319) and the second group (59).

To find the unit digit of the cube root, we have to find the cube that has the unit digit equal to the unit digit of the first group.

\({9^3} = 729\)

The cube of 9 has the unit digit 9, so our unit digit of the cube root is 9.

Now take the second group 59 and find the cube root that is just smaller than 59.

\({3^3} < 59 < {4^3}\).

27 or \({3^3}\) is just smaller than 59, hence our tenth place digit is 3.

Hence, the cube root of 59319 is equal to

\(\sqrt {59319}  = 39\)

Summary

When we hear the word cube root, the first two words that come to mind are cube and roots. In this sense, the concepts are somewhat similar; “root” refers to the primary source of origin. As a result, we only need to consider “which number’s cube must be chosen to get the given number.” The cube root of any number is the factor that is multiplied three times to obtain the specific values. Keep in mind that a number’s cube root is the inverse of the number’s cube.

When we say n is a cube root of m, then we can denote it as \(\sqrt[3]{m} = n\), with a small 3 written on the top left of the sign. The radical sign \(\sqrt[3]{{}}\)  is used as a cube root symbol for any number. Another way to express cube root is to write 1/3 as a number’s exponent. In cube roots, negative values are allowed, unlike in square roots,

For example, \(\sqrt[3]{{ – 216}} =  – 6\)

If you’re struggling with the concept of finding the cube root of a number, don’t worry – we’re here to help! Check out our video lesson no. 15 in 88guru’s online Math tuition for 8th class students.

Frequently Asked Questions

1. State the definition of cube root.

Ans: The cube root of any number is the factor that is multiplied three times to obtain the specific values. Keep in mind that a number’s cube root is the inverse of the number’s cube.

2. How is a cube root different from a square root?

Ans: A cube root is a number that when cubed yields the wanted number, whereas a square root yields the wanted number when squared. Furthermore, in cube roots, negative values are allowed, unlike in square roots.

3. What is the name of the method used for finding cube roots?

Ans: The prime factorization method is used to calculate the cube root of a number.

4. What is the cube root of 125?

Ans: 125 is a perfect cube, and 5 is the cube root of 125.

5. How Can a Cube Root Be Simplified?

Ans: The prime factorization method can be used to simplify the cube root. First, prime factorize the given number and then extract the common factors in groups of three. To find the answer, multiply these common factors by two.