Introduction
Set theory is a branch of mathematics that is based on logic, and it refers to the study of sets, i.e., groups of objects. The study of sets is most commonly used in the statistical field. One concept that can be used to better understand is the complement of sets, which refers to a group of objects that are not present in the given set. Studying complements of sets becomes much easier if we make use of De Morgan’s law.
In this article, we will attempt to understand what complements of sets are, what De Morgan’s theorem is, and how it can be used to study complement of sets. It must be noted that De Morgan’s theorem is also a theorem in electronic circuits or Boolean algebra and the two must not be confused.
De Morgan’s Law
In set theory, De Morgan’s law refers to two transformation rules that govern complements of sets. It allows us to easily work with set theory since sometimes, calculations become much simpler and easier after applying De Morgan’s theorem.
De Morgan’s law of Union – (A∪B)’= A’ ∩ B’
This law states that the complement of the union of two sets is equal to the intersection of complements of the two sets. Graphically, this is represented in the figure below:
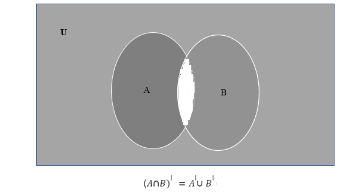
De Morgan’s law of intersection – (A∩B)’ = A’ ∪ B’
This law is simply the inverse of the previous theorem. It states that the complement of intersection of two sets is equal to the union of the complements of the two sets. You can see it in the figure below:
(A∩B)’ = A’ ∪ B’
What is the complement of a Set?
The complement of a set is defined as the set that includes all elements that are not present in A. That is, it can be considered to the opposite of a given set. If a set of fruits contains all bananas in the world, its complement will contain all fruits that aren’t bananas.
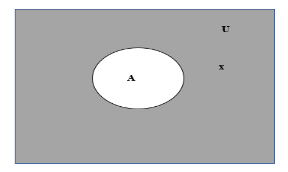
Graphically, consider a set A, which is a subset of the universal set U as shown below
Here, the complement of A can be defined as all elements that are not in A. Naturally, these elements will still be a part of U. Thus, we have the following definitions for the complement A’:
A’ = {x: x ⊄ A}
A’ = U – A
Complement of a Set Properties
There are a few properties of complements of sets that one must remember. These are listed below:
- The union of a set with its complement yields the universal set. That is, A ∪ A’ = U.
- The intersection of a set with its complement yields the null set Ø. Mathematically, A ∩ A’ = Ø.
- The law of double complementation states that the complement of the complement of a set gives us the original set itself. (A’)’ = A.
- The universal set contains all elements in the universe and the null set contains no elements. Thus, the universal and null sets are complements of each other. Therefore, Ø’ = U, and U’ = Ø.
Here are some examples to demonstrate these properties. Let U = {8, 9, 45, 89, 54, 25, 32} and A = {45, 54, 32}. Then, we see that A’ = {8, 9, 89, 25}. Therefore:
- A ∩ A’ = {45, 54, 32} ∩ {8, 9, 89, 25} = Ø (No common elements).
- (A’)’ = {8, 9, 89, 25}’ = {45, 54, 32}.
Solved Problems
1. Let U = {4, 38, 56, 100, 20, 12, 69}, A = {4, 56, 12}, and B = {20,69}. Prove De Morgan’s theorem for these sets.
Let us calculate the union of A and B. We get:
A ∪ B = {4, 56, 20, 12, 69}
(A ∪ B)’ = {4, 56, 20, 12, 69}’ = {38, 100}
Further,
A’ = {38, 100, 20, 69}
B’ = {4, 38, 56, 100, 12}
A’ ∩ B’ = {38, 100}
Similarly, for the second law, we have:
A ∩ B = Ø
(A ∩ B)’ = Ø’ = U
Now,
A’ ∪ B’ = {4, 38, 56, 100, 20, 69, 12} = U
Thus, we have proved De Morgan’s law.
2. If U is the universal set containing students who passed in their exams, and A is a subset containing those students who passed in Physics. If U contains 100 elements, and A contains 30 elements, how many students failed in physics?
We know that A’, the complement of A, contains all students who failed physics. Thus, we have
A’ = U – A
A’ = 100 – 30 = 70
Therefore, 70 students failed physics.
3. If A is the set of odd numbers less than 20, U is the set of all natural numbers less than 21, what is the complement of A?
We can write
U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20}.
A = {1, 3, 5, 7, 9, 11, 13, 15, 17, 19}
The complement of A is all elements not in A but not in U. That is, A’ = U ∩ A = {2, 4, 6, 8, 10, 12, 14, 16, 18, 20}.
Summary
This article was focussed on discussing the complements of sets, their properties, and De Morgan’s law. De Morgan’s law includes a pair of statements, which may be summarised by the rule of thumb “break the line, change the sign”. These rules are particularly useful for studying set complements.
Frequently Asked Questions
1. What will be the intersection of two null sets?
The intersection of two null sets leads to the null set itself.
2. What will be the union of a set with itself?
Union is defined as the collection of all elements that are present in both the sets and thus, the union of a set with the set itself leads once again to the set itself.
3. What is the relation between the set of integers and the set of whole numbers?
Integers contain all negative numbers as well while whole numbers do not contain negative numbers. Thus, the set of whole numbers is a subset of the set of integers.
4. Do sets obey commutative, additive, or distributive laws?
Yes. These laws are defined in the concepts of set algebra and are followed by sets in general.