Tag: Applications

Introduction

Electronics is a branch of physics that focuses on the behavior of electrons in electronic circuits. Unlike classical electrical engineering, electronics employ active devices as components. Note that active devices are devices that can control the flow of electricity in a circuit. On the other hand, passive components only consume electricity but cannot regulate it. Vacuum tubes which have the ability to control the flow of electrons, were initially fundamental to electronics but that technology is now obsolete. Today, you can create much more intricate circuits in much smaller form factors using transistors. 

An electric circuit is a closed path through which electric current can flow. Electrical components such as transistors, resistors, capacitors, and inductors are utilized in these circuits. Electronic devices, including computers, are constructed from thousands of electric circuits composed of these electronic components.

What is oscillation?

You have already come across hundreds of oscillations in your daily life. The term “oscillation” refers to the repetitive to and fro motion of a device or quantity. When a particle oscillates, it vibrates about an equilibrium position periodically. Common examples of oscillation you might be familiar with include the pendulum of a clock, your heartbeat, and the movement of strings in musical instruments. The pendulum moves to and fro from its mean position. Similarly, in a slinky, the spring extends and contracts rhythmically. An oscillation can be represented using a sine wave, whose value itself oscillates about 0. Oscillations can be free, damped, or forced.

Inductor

An inductor is a passive electronic component that converts electrical energy into magnetic energy and stores it. It is made up of a coil of wire that is generally wrapped around a given core but can be made without a core as well. An inductor works on the principle of electromagnetic induction, which is related to the generation of a magnetic field due to a changing current. 

Since an inductor is in the form of a coil, when current going through it changes, the loops of the coil resist the corresponding change in magnetic field. A quantity that characterizes inductors is the inductance. It is defined as the ratio of induced EMF to the change in current over time. The figure below shows a few common inductor types:

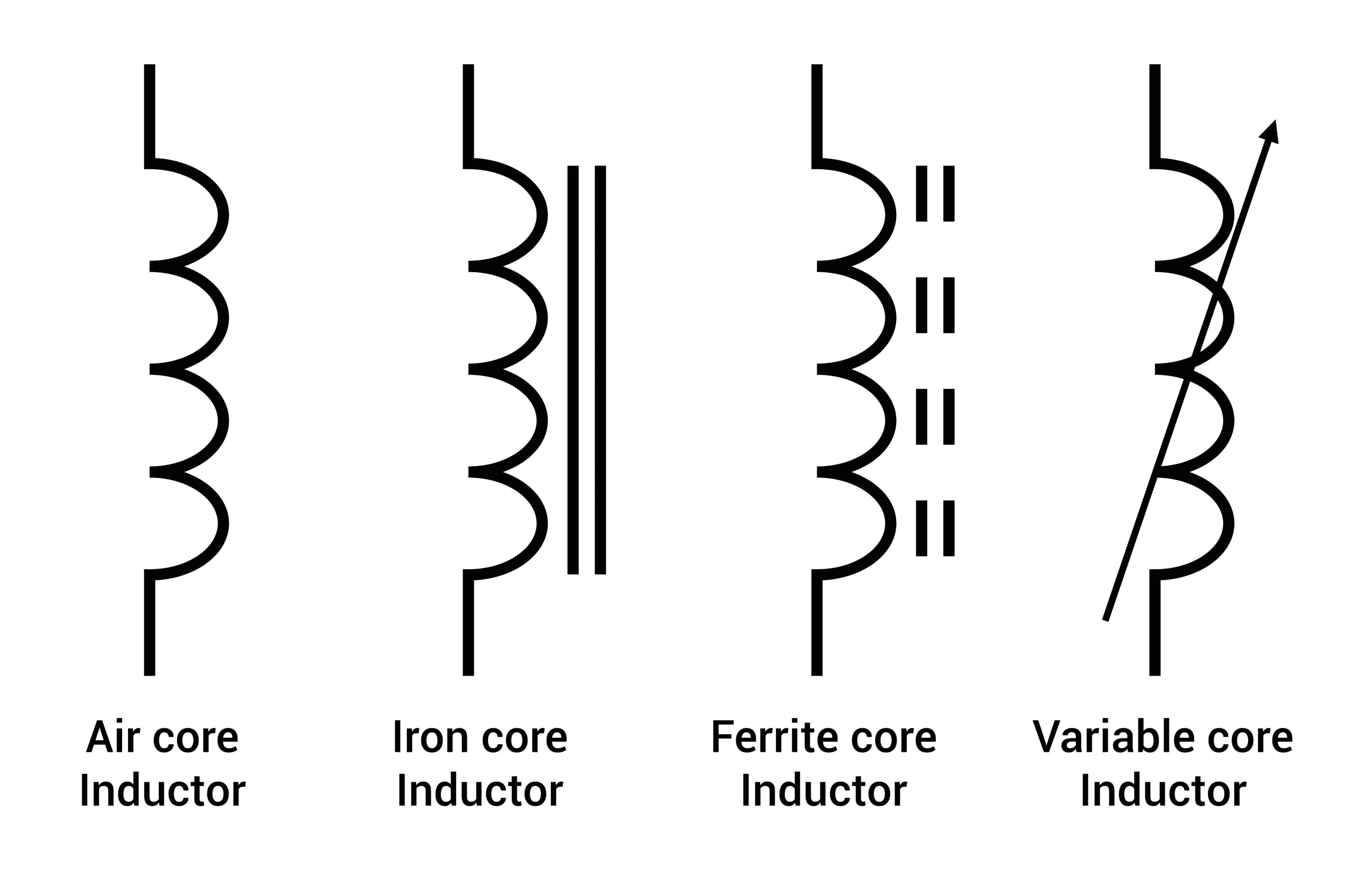
Inductor types

The increase in current creates a magnetic field in the inductor. This magnetic field reduces when the current through it decreases and the energy stored in the magnetic field is converted into electrical energy. Thus, an inductor can store energy in the form of a magnetic field.

Capacitor

Capacitance is the ability to store electric charge and capacitors are devices that facilitate this. Generally, they are made of two conducting plates separated either by air or by some other dielectric material like ceramics, plastics, mica, etc. 

When a capacitor is connected to a DC source, electrons move from the negative terminal and accumulate on the conducting plate, inducing a positive charge on the other plate. The dielectric material in between the plates prevents electrons from crossing the barrier. This way, electrons get stored on the plates and the energy thus stored can be utilized later. Mathematically, capacitance is measured using the following formula:

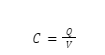
The following diagram shows a capacitor:

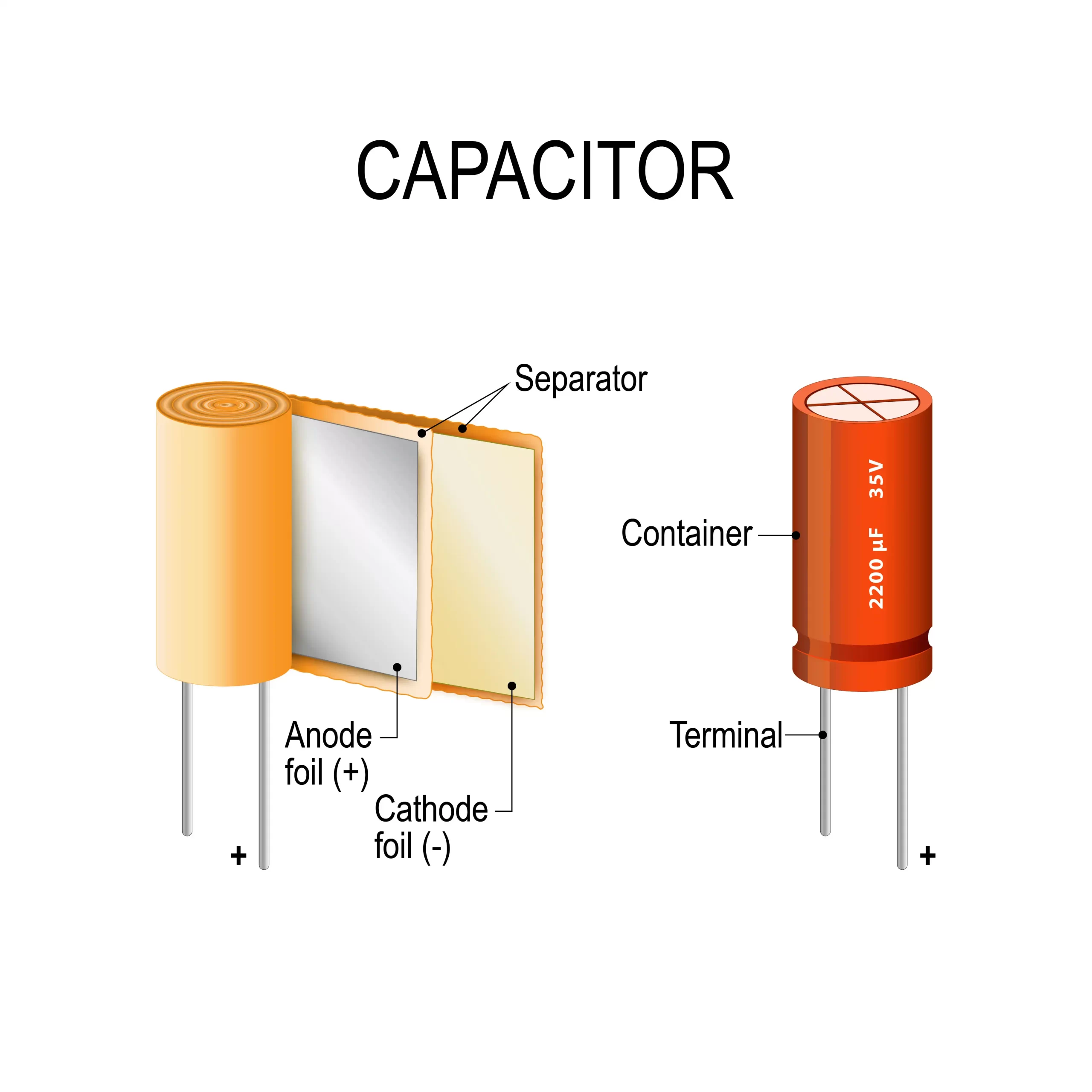
Capacitor

LC oscillator

An LC circuit is so named because it contains an inductor and a capacitor. Capacitance is depicted by C while inductance is depicted by L, hence the name LC circuit. An LC circuit is also sometimes referred to as a tank circuit. An LC circuit can act as a resonator that stores energy and then oscillates at a particular frequency using positive feedback without external influence.

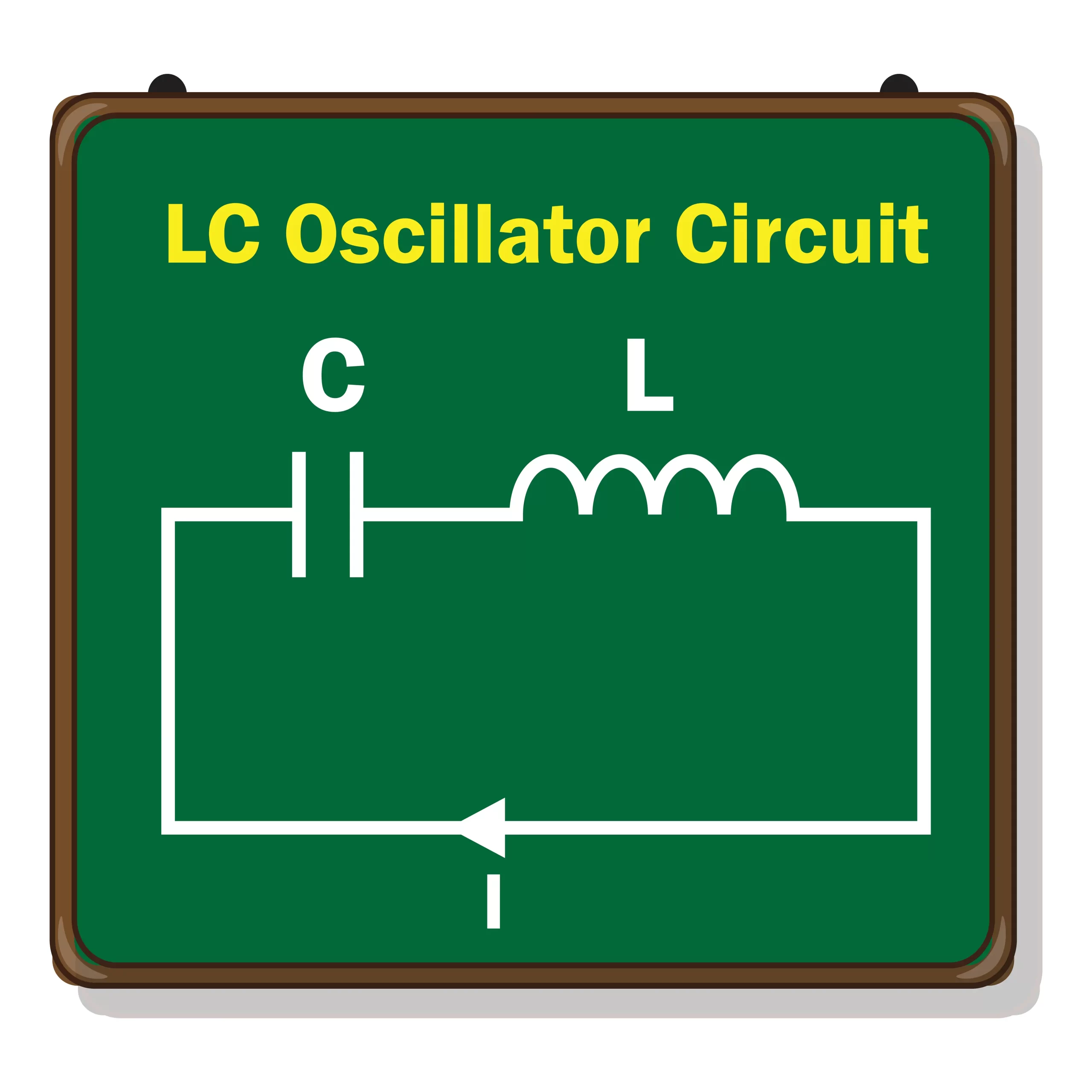
LC Oscillator

Working of LC oscillator

1. In the circuit depicted in the figure above, we have an inductor and capacitor connected in series.
2. When voltage is applied, the capacitor starts developing a charge. In this time period, the inductor does not receive anything.
3. When the applied voltage is removed, the energy stored in the capacitor flows to the inductor and the capacitor discharges.
4. Once the capacitor has been completely depleted, the inductor carries all the energy and it removes it into the circuit. This charges the capacitor in the opposite direction till all energy is transferred to it.
5. This cycle repeats to give rise to LC oscillations.

Applications

LC oscillators find a wide range of applications in electrical circuits. Here are a few examples.

1. They are used in AC-DC converters.
2. They are used in amplification circuits.
3. Radios, TVs, transmitters, filters, etc. all utilize LC circuits.
4. They are used for induction heating.
5. They are used in sine wave generators.

Summary

Capacitors store charge while inductors store magnetic energy. When connected in series, they can be used to create oscillator circuits which do not require external influence to operate. This article discussed concepts related to LC oscillator circuits in detail.

 

Frequently asked questions

1. What are free and forced oscillations?

Free oscillations occur when an oscillating body is allowed to oscillate without external influence. On the other hand, one can force a body to oscillate continuously using an external force, which is known as forced oscillations.

2. Differentiate between damped and undamped oscillation?

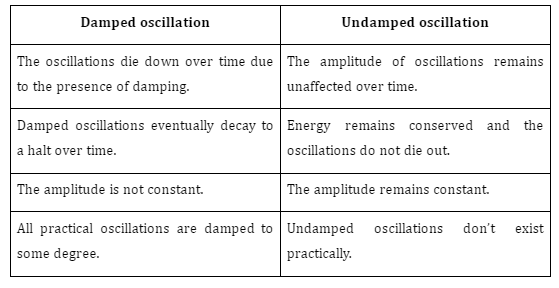
3. What are the applications of inductors?

Inductors find a wide range of applications, a few of which are:

1. Choking, blocking, filtering, or smoothening high frequency noise.
2. Used in oscillators.
3. Used in power converters.
4. Used in radios, TVs, wave generators, etc.

4. What are the differences between the capacitor and inductor?

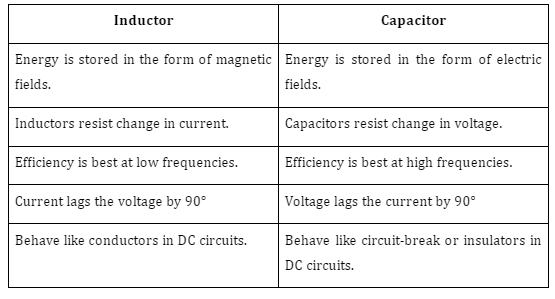
5. What are the uses of capacitors?

1. Capacitors are used for quick release of electric charges. This is used in camera flashes, keyboards, etc.
2. Capacitors can be used to detect high frequency electromagnetic radiation.
3. Ignition systems use capacitors.
4. Oscillators, amplifiers, and transmitters utilize capacitors.

Introduction

The relationship between two expressions on either side of the equal to sign is represented by an equation in mathematics. One equal symbol and one variable are used in this kind of equation. Simple equations use arithmetic operations to balance the expressions.

A simple equation is an equation that shows the relationship between two expressions on both sides of the sign. Only one variable appears in these kinds of equations, either on the first side or the other side of the equal symbol. For instance, 83 = 5 – 4z. In the provided example, the variable is z. Simple equations use arithmetic operations to balance the expressions on both sides. Linear equations in one variable are also regarded as simple equations.

Equations

Equations are relationships between two or more expressions connected by the equals sign, or “=.” Variables, coefficients, and constants are the three components of an equation.

Variables: Variables are the names given to the symbols (typically English alphabets) that are assigned to an arbitrary, unknowable value.

Coefficients: The coefficients of a term are the numbers that are multiplied by a variable or the product of two variables in that term.

Constants: Constants are the numbers that are independent of variables.

Simple Equations

A type of equation known as a simple equation compares two linear expressions with just one variable in common. Several instances of basic/simple equations are

3x + 4 = 7

4x + 5 = 3x + 8

Since many of the situations, we encounter in real life can be formulated as simple equation problems, we can use simple equations to obtain the desired results in a variety of areas of life.

Simple Equations questions

Simple equation problems, which can be represented by a simple equation to find the value of something unknown based on some given conditions, are known as simple equation questions. One such example of applying simple equations to real-world situations is provided, 

Let’s say Amar and Bipin, two friends, are purchasing apples. Amar might have purchased 5 kg and Bipin 3 kg. If Amar paid Rs. 80 more than Bipin, we must determine the cost of a kg of apples. The following simple equation can be used to represent this situation:

5x = 3x + 80, where x is the price of 1 kg apples.

Solving Simple Equations

To answer questions involving simple equations, we change the equation so that the term with the variables is on one side of the equation and the term with constants is on the other. We then simplify both sides so that there is only one term on each side, one with variables and the other with constants.

The value of the variable is then obtained by simply multiplying the equation by the reciprocal of the coefficient.

Now, let’s look at some examples to help us better understand it.

Example: Solve the following simple equation, 5x – 20 = 3x + 60

Solution: Here we have 5x – 20 = 3x + 60

Adding 20 to both sides while subtracting 3x to move terms with variables to one side and constants to the other.

⇒ 5x – 20 + 20 – 3x = 3x + 60 + 20 – 3x

⇒ 5x – 3x = 60 + 20

⇒ 2x = 80

Dividing by 2 on both sides

⇒ x = 40

Simple Equation Problems

Simple equation problems are mathematical issues from the real world that are modelled by simple equations. We must first determine the number of arbitrary values present and their relationships to represent a given situation using a simple equation. If there is only one arbitrary value, it is easy to create a simple equation to describe it; however, if there are several arbitrary values, we must establish a direct relationship between them to do so.

Example: Determine whether the following scenario can be modelled as a simple equation or not. Amit is currently twice as older than his younger brother Sagar. The combined age of Amit and Sagar was 23, two years ago. Identify their current ages.

Solution: Since Amit’s age and Sagar’s age are arbitrary values, the only way we can depict this situation in a simple equation is if there is a direct correlation between their ages, which is implied by the first statement that Amit is currently twice as old as Sagar. As a result, we can express this as a simple equation problem.

Let Sagar’s present age be x years

And Amit’s present age be y years

Then, ATQ

In present, y = 2x

Also, two years ago, (x – 2) + (y – 2) = 23

Substituting y = 2x in the second equation,

⇒ x – 2 + 2x – 2 = 23

Equations in Everyday Life Examples

When a value for a quantity or identity is unknown in a real-world situation and cannot be determined by a simple mathematical operation, linear equations are used, such as when estimating future income, forecasting future profits, or figuring out mileage rates.

Here are a few real-world instances where applications of linear equations are used.

• Can be used to identify age-related problems.
• It is used to determine the distance, duration, and speed of a moving object.
• It is used to resolve problems involving money, percentages, etc.

Solved Examples

Example: Calculate the value of y from the equation:  – 5 = 6.

Solution: We will simplify the equation first by separating the variables and constants,

– 5 = 6

Add 5 on both sides,

⇒  – 5 + 5 = 6 + 5

⇒  = 11

Multiply by 3 on both sides,

⇒  x 3 = 11 x 3

⇒ 11y = 33

Divide by 11 on both sides,

⇒ y = 3

Summary

Simple equations are also known as linear equations when they contain multiple variables and can be resolved using a variety of techniques. To solve problems from daily life, such as how to measure an unknown length, etc., we use simple equations. The typical method of representing the relationship between variables is through simple equations. A simple equation is a linear equation that only has one variable. Simple equations were credited to Rene Descartes as their creator. One of the foundations of algebra is simple equations.

Frequently Asked Questions (FAQs)

1. What are Linear Equations?

Linear equations are the mathematical relations that relate two expressions of degree 1 with the equal to symbol.

2. What are Simple Equations?

Simple equations are linear equations that have only one variable. Simple equations can be solved easily and are very useful in many days to day life problems.

3. What are the different methods of Solving Simple Equations?

There are two ways that we can solve simple equations. The techniques are the systematic method and the trial-and-error method.

4. What is a Rational Expression?

A rational expression is expressed in terms of the fraction of two algebraic expressions, and it also belongs to the class of simple equations.