Introduction
Pythagoras, a Greek philosopher who was born around 570 BC, is remembered by the theorem’s name. The theorem has likely been proved the most times of any mathematical theorem using a variety of techniques. The proofs are numerous, some of which go back thousands of years, and include both geometric and algebraic proofs. The Pythagorean theorem is extremely useful when determining the shortest distance between two points or the degree of the mountain slope. In a right-angle triangle the square of the hypotenuse is said to be equal to the sum of the squares of the two legs.
Right Angle Triangle
A triangle with a right angle is one in which one angle is 90 degrees. We refer to this triangle as a right-angle triangle since 90 is also referred to as the right angle. Triangle sides with a right angle were given unique names. The side directly opposite the right angle is known as the hypotenuse. Based on the values of the various sides, the right triangles are divided into isosceles and scalene types.
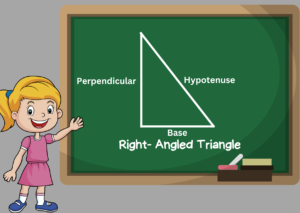
Properties of Right-Angle Triangle
- The height, base, and hypotenuse of a right-angle triangle are its three sides.
- The two adjacent sides are referred to as base and height or perpendicular.
- Three similar right triangles are formed if we draw a perpendicular line from the vertex of a right angle to the hypotenuse.
- The radius of a circle whose circumference includes all three vertices is equal to one-half the length of the hypotenuse.
- The triangle is known as an isosceles right-angled triangle, where the adjacent sides to the 90° are equal in length if one of the angles is 90° and the other two angles are each equal to 45°.
Pythagoras Theorem
Pythagoras is a potent theorem that establishes the relationship between the sides of a right-angle triangle. According to Pythagoras’ theorem –
“Square of the hypotenuse is equal to the sum of the square of the other two legs of the right angle triangle”. Mathematically, it may be expressed as
Hypotenuse² = Perpendicular² + Base²

Area of the Right-Angle Triangle
The area of the right-angle triangle is the region enclosed within the triangle’s perimeter. The formula for a right-angle triangle’s area is.
Area of right-angle triangle = ![]() (Base × Perpendicular)
(Base × Perpendicular)
Facts
- A triangle must be a right triangle if it obeys Pythagoras’ theorem.
- The longest side of a triangle is the one that makes the largest angle.
- When the midpoint of the hypotenuse of a right-angled triangle is joined to the vertex of the right angle, the resulting line segment is half of the hypotenuse. In other words, the center of the hypotenuse is the circumcenter of the right-angled triangle.
- If two sides of a right angle are known, we can find the other side using Pythagoras’ Theorem.
- From the provided value of sides, we may determine whether a right-angle triangle is possible.
Summary
A right-angled triangle is one in which one of the angles is a right angle (90 degrees), and the hypotenuse is the side opposite to the right angle. The hypotenuse square of a right-angled triangle is equal to the sum of the squares of the other two sides, according to Pythagoras’ Theorem.
Solved Examples
Example 1: In the right-angle triangle, If PQ = 5 cm and QR = 12 cm, then what is the value of PR?

Solution: By Pythagoras theorem, we have,
Hypotenuse² = Perpendicular² + Base²
PR² = 5² + 12²
PR² = 25 + 144
PR = ![]() = 13 cm
= 13 cm
Hence, the value of PR is 13 cm.
Example 2: If a triangle has three sides 9cm, 5 cm, and 7 am respectively, check whether the triangle is a right triangle or not.
Solution: According to the theorem, if the square of the longest side equals the sum of the squares of the other two sides, a triangle is said to be, a right triangle.
9² = 5² + 7²
81 = 25 + 49
81 ≠ 74
Thus, 81 is not equal to 74. Hence, the given triangle is not a right-angle triangle.
Frequently Asked Questions
1.Which Side of a Right-Angled Triangle is the Longest?
Ans: The hypotenuse of a right-angled triangle is its longest side.
2.What is a Right-Angled Triangle’s Perimeter?
Ans: The perimeter of a triangle is the sum of all sides.
Perimeter = base + perpendicular + hypotenuse.
3.Can there be two Right Angles in a Triangle? Explain.
Ans: No, there can never be two right angles in a triangle. A triangle has exactly three sides and interior angles that add up to 180 degrees. This means that if a triangle contains two right angles, the third angle must be zero degrees, which means that the third side will overlap the opposite side. Therefore, a triangle with two right angles is not possible.