Tag: Algebraic Expressions

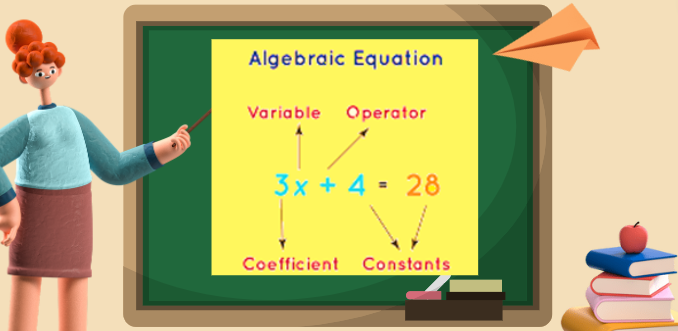
An Introduction

The value of a variable determines the value of an expression. By substituting the variable’s value in the expression and utilizing mathematical procedures, the expression is made simpler. The expression’s value is the outcome that is ultimately obtained. A whole integer, rational number, decimal number, or real number can be the value of the expression. A component of algebra is the expressions. A mathematical expression is made up of a mixture of numbers, variables, and operators. Any number of terms can combine to produce it. Any phrase may have any number of terms, ranging from 1 to n.

Find the value of the expression.

A phrase uses a variety of words. Any expression’s terms are the result of its variables and numbers. As the value of the variable changes, so do the terms’ values. Any number may be the value of the variables. As a result, the expression’s value changes together with the variable’s value. Any number of variables can be used to determine the value of the expressions. The expressions can be rationalized, factored, simplified, or enlarged to get at the answer. An expression’s value can be determined by substituting the values of its variables and then solving the expression. Only the phrasing of the expression determines its value. The value of the expression will always be a positive real number if it is the sum of two positive variables. The expression created by the product of the three negative variables will also always have a value that is a negative real number. Although it is the only possible value for the expression, the value of the variable is always a factor. The values of the variables must therefore be known in order to determine the expression’s value.

Find expression

Any expression is a concatenation of phrases related to mathematical operators +,-, etc. The terms of the expression serve as a clue. Any mathematical expression’s terms must include both numbers and variables. The English alphabets serve as a representation of the variables. Examples of the variables include, x,y,z,a,b,c and others. Defining the terms will help you find the expressions. Below are a few instances of these expressions.

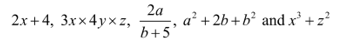
Expression in Mathematics

In algebra, expressions are one of the fundamental ideas. Expressions help you create equations, solve equations, comprehend fundamental principles of functions, and create various forms of equation solutions. Therefore, it is crucial to grasp expressions in mathematics. Expressions may contain a single variable or several variables. Mathematics uses like and unlike terms in its expressions. Finding similar and dissimilar terms in any expression is crucial since doing so simplifies complex statements. By looking at the variables in the following expressions, it is possible to determine the like terms and unlike terms of any mathematical equation. The expressions’ like terms all contain the same variables. On the other hand, there are various variables in the variable portion of the variables. For two words to be similar, their respective variable powers must be equal. Below are a few examples of mathematical expressions.

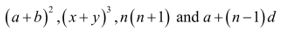
What is an expression in Mathematics?

Mathematical expressions are a collection of terms made up of variables and integers related by the addition, subtraction, multiplication, and division mathematical symbols. After learning how to calculate an expression’s value and identify an expression, explain what an expression in mathematics is. There are many identities in the study of mathematics. Two equivalent formulations make up the identity. For all possible values of the variables, the two sides of the identities are always equal. Following are explanations of a few mathematical expressions.

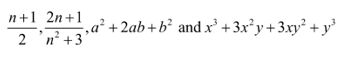
Interesting Facts

• There is never a match between the equations and the expressions.
• Expressions can be made simpler by factoring them, rationalising them, eliminating common terms from the numerator and denominator, and adding and subtracting.
• Only when the values of the variables are equal can two straightforward expressions in the same variable have values that are equal.

Solved Problems

1. Find the value for the expression a+4 when, a=2 and -2.

Sol:

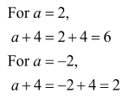
2. Calculate the value for the expression given below for x=1 and 2.

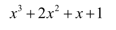
Sol:

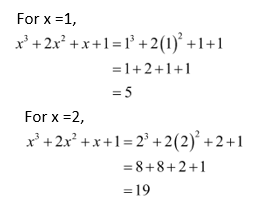
3. Simplify the expression \({y^2} + 3y\) and find its value at y = 0..

Sol: Factorize the given expression.

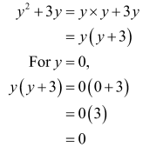
Summary

The expressions are used in mathematics to represent a certain value for different particular values of the respective variables. The variables can be any real values. To find the value of the expression, substitute the values of the variables and then simplify the obtained arithmetic expression. Expression is a combination of the terms with the mathematical operators. To find the expression, identify the terms and check if their combination is an expression or an equation. Expression in Mathematics is used frequently. The expression in mathematics helps to form different numbers of identities.

Practice Questions

Solve the expression x + y for x = 1, y = 2 and x = -2.5 , y = 0

Ans: 

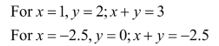
2. Simplify the expression \(\frac{{{x^3} + 2x}}{{3{x^2} + x}}\)and find its value at x =1.

Ans:

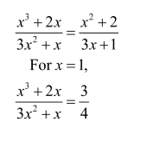
Frequently Asked Questions

1. Are the expressions and equations always the same?

Ans: No. They are not the same.

2. What is the use of expressions in mathematics?

Ans:  Any general rule which is true for different sets of numbers can be represented using the expression.

3.  Can two sets of variables have the same value for the expression?

Ans: Yes. Two sets of variables can have the same value for the expression.

Introduction

An expression made up of variables, constants, coefficients, and mathematical operations like addition, subtraction, etc. is known as an algebraic expression. Algebraic expressions have several uses, including describing real-world issues and solving various and difficult mathematical equations, calculating income, cost, etc. There are two categories of words in algebra: like terms and unlike terms. Unlike terms are merely the opposite of like terms in that they do not share the same variables and powers. Like terms are those that have the same variables and powers.

Algebraic Expressions

An expression made up of variables, constants, coefficients, and mathematical operations like addition, subtraction, etc. is known as an algebraic expression. A variable is a symbol without a predetermined value. A term is either a variable, a constant, or both joined by mathematical operations. A coefficient is a quantity that has been multiplied by a variable and is constant throughout the whole problem. Based on a variety of terminology, there are three primary categories of algebraic expressions: monomial, binomial, and polynomial. Terms can also be divided into similar and dissimilar terms.

Also see: Online Tuition for Class 6 Maths

Terms in algebra

A term can be a number, a variable, the sum of two or more variables, a number and a variable, or a product of both. A single term or a collection of terms can be used to create an algebraic expression. For instance, \({\bf{2x}}\) and \({\bf{5y}}\) are the two terms in the expression \({\bf{2x + 5y}}\) .

A mathematical expression has one or more terms. A term in an expression can be a constant, a variable, the product of two variables \({\bf{\left( {xy} \right)}}\) or more \({\bf{\left( {xyz} \right)}}\) , or the product of a variable and a constant \({\bf{\left( {2x} \right)}}\) , among other things.

Also Read: Terms of an Expression

Terms in an algebraic expression

A term is a group of numbers or variables that have been added, subtracted, divided, or multiplied together; a factor is a group of numbers or variables that have been multiplied; and a coefficient is a number that has been multiplied by a variable. Three terms, \({\bf{9}}{{\bf{x}}^2}\) ,\({\bf{x}}\)  , and \({\bf{12}}\), make up the expression \({\bf{9}}{{\bf{x}}^2}\)+\({\bf{x}}\) + \({\bf{12}}\)

By drawing this conclusion, it is clear that an expression is made up of a number of terms, variables, factors, coefficients, and constants.

Types of Terms 

There are different types of terms in algebraic expressions,

Variables

These types of terms are usually represented by an symbol (most commonly its english alphabets), like \({\bf{x}}\), \({\bf{y}}\), \({\bf{z}}\), \({\bf{a}}\), \({\bf{b}}\), etc. these symbols are there to represent unknown arbitrary values, hence the name ‘variables’ (since their values can vary).

Coefficient

These are not a type of a term but rather a part of a term that contains variables, coefficients are the numbers that are in multiplication with variables.

Constants

These terms are the numbers separate from the variables, and as the name suggest, they are a constant number, i.e., they are fix and never change unless they are under an operation with another constant term.

Like and Unlike Terms

Like terms in algebra are the kinds of terms that share the same kinds of variables and powers. There is no requirement that the coefficients match. When a term has two or more terms that are unlike terms, it means that those terms do not share the same variables or powers. Before there is power, the order of the variables doesn’t matter. Consider the example of similar and dissimilar terms.

Like Terms: \({\bf{3x}}\), \({\bf{-5x}}\) are like terms

Unlike Terms:\(\;{\bf{2}}{{\bf{x}}^3},{\bf{7}}{{\bf{x}}^2}\)  and \({\bf{5y}}\)  are all unlike terms.

Like Terms

Terms with the same kinds of variables and powers are referred to as like terms. It is not necessary to match the coefficients. The coefficient could differ. To obtain the answer, we can simply combine like terms, or we can simplify the algebraic expressions. In terms of the same types of variables and powers, the results are very easily obtained in this way.

The evaluation of straightforward algebraic puzzles is an example of similar terms.

Unlike Terms

In algebra, unlike terms are those terms that do not share the same variables and cannot be raised to the same power.

For instance, in algebraic expressions, \({\bf{4x}} – {\bf{3y}}\) are unlike terms. because \({\bf{x}}\) and \({\bf{y}}\) are two different variables. Due to the lack of \({\bf{x}}\) and \({\bf{y}}\) values, it cannot be simplified.

Summary

An expression made up of variables, constants, coefficients, and mathematical operations like addition, subtraction, etc. is known as an algebraic expression. Coefficients, constants, and variables are a few of the key words in the context of algebraic expressions. Similar terms are those in algebraic expressions that are constants or involve similar variables raised to similar exponents. In algebraic expressions, unlike terms are those terms that do not share the same variables or that share the same variables but have different exponents. Algebraic expressions are all polynomials, but not all algebraic expressions are polynomials. Polynomials are algebraic expressions without fractional or non-negative exponents. Algebraic expressions include fundamental identities that are used in the subject.

Tips to Prepare for Class 6 Maths

FAQs

What are polynomials?

Polynomials are algebraic expressions with more than \({\bf{2}}\) terms and the variables have non-negative integer exponents.

What is a quadratic equation?

A quadratic equation is a polynomial equation, with maximum exponent on a variable being \({\bf{2}}\).

What is a term in an algebraic expression?

A term can be a number, a variable, the sum of two or more variables, a number and a variable, or a product of both. A single term or a collection of terms can be used to create an algebraic expression.