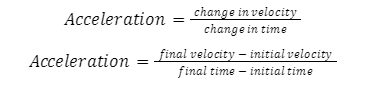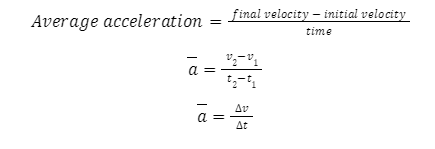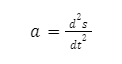Tag: Acceleration

Introduction

In physics, there are two types of physical quantities: those that contain a direction as well as magnitude and those that contain only direction. The former are known as vector quantities and the latter are known as scalars. Time, temperature, mass, etc. are scalar quantities since there is no physical sense for mass to have direction. On the other hand, velocity, acceleration, force, etc. are quantities whose directions are important and thus, are examples of vectors.

The process of determining the magnitude and where applicable, the direction of a quantity is known as measurement. It yields a numerical value along with a direction if required. Measuring quantities also requires a standard set of units with reference to which, we can give their numerical value. For instance, we know our height to be 160 cm only because we have a reference value for how long 1 cm is. For this end, the SI system of units was developed to provide a global standard.

What is speed?

Speed measures the pace at which an object moves with reference to a reference point. When we talk of speed in physics, we are concerned with only the distance covered and do not inquire about the direction. Thus, speed is a scalar quantity. Mathematically, we can write:

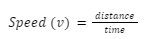
In the SI system of units, speed is measured in m/s whereas the cgs system measures it in cm/s. Other common units include km/h, mph, etc.

Apart from moving in a straight path, objects can also move along a circular path in which case, we can measure their angular speed in terms of the angle they sweep out in a given time interval. Mathematically,

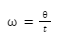
Types of speed

Physicists classify speed into various types depending on different criteria. Here are a few common classifications:

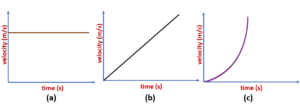
Uniform speed

An object is said to possess uniform speed if the speed remains constant in time. That is, even as time passes, its speed does not change.

Variable speed

Objects whose speed is not constant in time are said to be moving with a variable speed.

Average speed

We know that it is practically difficult for objects to keep moving at exactly the same speed over time. But over the course of a journey, one can calculate an average speed which gives us a general idea about the motion of the object. 

Average speed is measured by taking the total distance that the object covered and dividing it by the total time it took to cover that distance. That is,

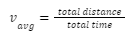
Instantaneous speed:

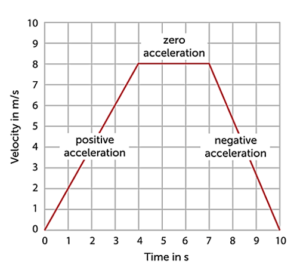
As previously mentioned, an object may have different speeds at different instants in time. The value of its speed at an exactly defined moment in time is termed as its instantaneous speed at that moment.

The calculation for speed

To calculate an object’s speed, we can simply apply the formula for speed. Thus,

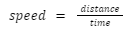
A few common examples of speeds measured by scientists include the speed of light in vacuum, which is approximately 3E8 m/s. On the other hand, the speed at which Earth rotates about its axis is 7.28E-5 rad/s and the speed at which it travels around the sun is given as 30 km/s.

Relation between angular speed and linear speed

We can derive a relation between the angular and linear speeds of an object. We know that linear speed is 

Further, we know that for circular motion, when the angle swept is very small, the arc length can be approximated as 

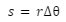
The angular speed is written as ⍵=θ/t. Hence, if we multiply both sides of this equation with r, we get:

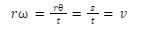
Thus, angular and linear speeds are related by the equation v=r.

Solved examples

1. Raju drives at 15 km/h for 3 hours. How much distance did he cover?

We know that 

2. If the blade of a fan rotates at an angular speed of 16π rad/sec, what is the time taken for one complete rotation.

Angular speed can be directly related to the time taken for one complete rotation (T) as follows:

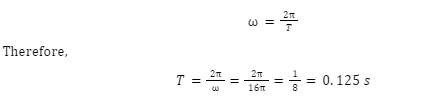
Hence, the fan completes one rotation in 0.125 seconds.

Summary

Speed is a scalar quantity that measures the pace at which an object is moving. It is measured by dividing the distance covered by the time taken to cover that distance. Angular and linear speeds can be related to each other.

Frequently asked questions

1. Describe Newton’s first law of motion.

Newton’s first law states that if an object is moving or at rest, it will continue in that state unless some external factor forces it to change its state of motion. Unless some external factor stops a ball from rolling, it will continue rolling.

2. How does the angular speed of an object remain the same at all points?

Angular speed measures the rate at which a certain amount of angle is swept by an object. It changes with radius and thus, remains the same for all points.

3. How does an ice skater control their angular speed?

Since angular speed depends on the radius, if the ice skater or ballet dancer pulls in their arm close to their body, they speed up. They can also reduce their speed by extending their arms. This is related to the law of conservation of angular momentum.

4. What instrument measures linear and angular speeds?

Linear speed is measured by speedometer in a car while angular speed is measured by an instrument known as tachometer.

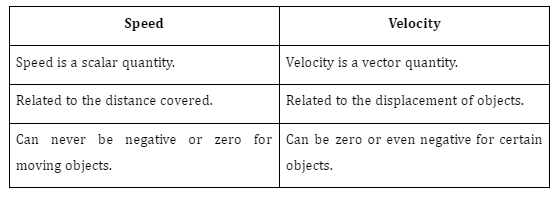
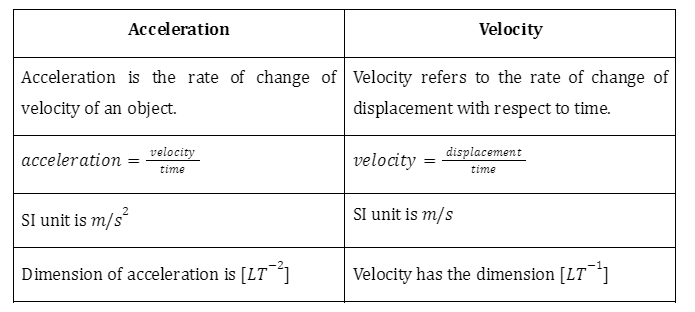
5. What is the difference between speed and velocity?

Introduction

Acceleration represents the change in velocity of an object. It can either be positive or negative, depending on whether the final velocity is greater or less than the initial velocity. Thus, if the velocity of an object is decreasing with time, it is said to possess negative acceleration or retardation. 

Acceleration is a vector quantity which has both magnitude as well as direction. During circular or rotational motion, the acceleration encountered is referred to as rotational acceleration. Note that it is possible for an object to have zero acceleration if it is moving with a constant velocity.

What is Acceleration? 

In simplest of terms, acceleration is the rate of change of an object’s velocity with respect to time. Hence, its SI unit is given as \(m/{s^2}\).

General Formula of Acceleration

Generally, acceleration can be calculated via the following formula:

Acceleration dimensional Formula in Physics

Acceleration Unit

This is the SI unit of acceleration and other derived units can be found in different systems.

Acceleration Types

Most generally, acceleration can be classified into the following types:

1. Uniform acceleration
2. Non-uniform acceleration

Uniform acceleration: An object whose velocity is changing at a constant rate is said to possess uniform acceleration.

Example: Suppose a car’s speed increases steadily by 30 m/s in 10s throughout a journey. That would mean that the car has a constant acceleration \(3m/{s^2}\).

Non-uniform acceleration: Non-uniform acceleration is acceleration which itself does not remain steady in time.

Example: Suppose that during the first 2 hours of a journey, a car travels with a velocity of 15 km/hr. In the next 3 hours, the velocity changes to 45 km/hr. The change in velocity occurs over unequal intervals of time and thus, over the course of the journey, the car has non-uniform acceleration.

A few other types of acceleration may be stated as follows:

Acceleration due to gravity: This is simply the acceleration experienced by a body due to the gravitational force. Mathematically, it is equal to the gravitational force per unit mass experienced by the object.

Centripetal acceleration: A body in rotational motion experiences this type of acceleration and it is given as the centripetal force per unit mass experienced by a body undergoing circular motion.

Radial acceleration: Acceleration directed along the radius for a body in circular motion is called radial acceleration.

Angular acceleration: Angular acceleration is also experienced by a body in circular motion and its effect is to change the angular velocity of an object.

Coriolis acceleration: Coriolis force comes into the picture when the frame of reference we are considering is itself rotating with a given velocity. The coriolis acceleration is the acceleration encountered due to this coriolis force.

Average acceleration

For a non-uniform motion, we can find out the average acceleration of the object in question to get an overall sense of how it may have moved over the course of its journey. It is defined mathematically as follows.

Instantaneous acceleration

The acceleration experienced by an object at a particular instant in time is referred to as instantaneous acceleration and it is given as the limiting value of the rate of change of velocity of an object when the time interval tends to zero.

Where a= acceleration of the body, s=displacement of the body, and t= time. Thus, instantaneous acceleration is the second derivative of displacement.

Negative acceleration or retardation: Acceleration that slows down the motion of an object is referred to as retardation. For such a phenomenon to occur, the acceleration applied must be negative.

Velocity-Time Graph

Acceleration can also be derived from the velocity-time graph of an object. The slope of the graph gives us acceleration as a function of time and if we find the value of this slope at a particular point, i.e., the slope of tangent at a point, we arrive at instantaneous acceleration. 

Graph for average acceleration

Graph for instantaneous acceleration

Graph for uniform acceleration

Graph for non-uniform acceleration

Examples of Acceleration

Example 1: A body moving with \(20m/{s^2}\) comes to a halt after 5.2 secs. Find the nature of acceleration and its value.

Solution: 

Example 2: If a car is moving with a velocity of 45 m/s and after 10 s, its velocity becomes constant at 60 m/s, find acceleration.

Solution:

Difference between Acceleration and Velocity

Summary

Acceleration measures the change in velocity of an object. Its SI unit is \(m/{s^2}\) and it is a vector quantity with both magnitude and direction. It can be determined as the first-order derivative of velocity or the second-order derivative of position vector.  An object moving with a constant velocity has zero acceleration since the derivative of a constant is equal to zero. 

Frequently Asked Questions

1. Give two examples of retardation.

Two examples of retardation are as follows:

1. A train that reaches a halt will slow down and thus, experience retardation.
2. A ball thrown upwards experiences retardation due to gravity.

2. What is the SI and CGS unit of acceleration?

In SI units, acceleration is measured in \(m/{s^2}\)  and in CGS units, in \(cm/{s^2}\).

3. What is gravitational acceleration?

Gravity is the force by which the Earth attracts a body towards its center. This force generates acceleration in a vertical motion, known as gravitational acceleration. The motion of an object falling solely under the effect of gravity is termed as free-fall.

4. What is the value of gravitational acceleration?

The approximate value of acceleration due to gravity is \(9.8m/{s^2}\).

5. What is angular acceleration?

Angular acceleration measures the time rate of change of angular velocity of an object and thus, is measured in \(rad/{s^2}\).

6. What is a Coriolis force?

Coriolis force is experienced by objects which are moving in a frame of reference that is itself rotating with a given angular velocity. It is responsible for wind in certain regions of the Earth.

Introduction

The rate of change in displacement of a moving object is referred to as its velocity. As a result, velocity is a vector quantity, and the velocity-time graph or velocity-time relation is a graphical representation of its fluctuation with time. A velocity-time graph shows the variation of the object’s velocity with time, under different conditions, such as under uniform motion, and under acceleration. On a velocity-time graph, acceleration is depicted by the slope of the graph line.

Velocity-Time Graph for Uniform Motion (No acceleration)

Since there is no acceleration being given to the moving object in this scenario, its velocity is constant and does not fluctuate over time. As a result, in this scenario, it is clear from Figure (a) below that despite the change in time, the velocity will remain constant throughout the entire journey of the object.

Velocity-Time Graph with a Constant Uniform Acceleration

In this situation, the item is subject to a constant uniform acceleration, so depending on the applied uniform acceleration—referred to as the accelerating and retarding acceleration, respectively—its velocity will constantly grow or decrease. We see a linear behaviour of the object’s velocity with time in the velocity-time graph (as shown below in Figure (b)), where the velocity of the item grows linearly on the application of constant uniform acceleration. You can use the slope of this graph to calculate the object’s applied acceleration.

The object’s equations of motion under a uniform constant acceleration can be expressed as follows:

v = u + at

s = ut + 1/2 at²

v² = u² + 2as

Where v, u, a, s, and t are the final velocity, initial velocity, uniform acceleration, total displacement of the object, and travel/trip time, respectively.

Velocity-Time Graph under a Variable Acceleration

As shown in Figure (c) above, in this situation, the acceleration acting on the object varies with time and as a result, the object’s variation in velocity is different during each time period of the journey. As a result, we observe a velocity-time graph that differs from the case where the object is subjected to variable acceleration and observe a parabolic behaviour of velocity with time.

Summary

The rate of change of displacement is known as velocity. The slope of the curves on the velocity-time graphs indicates how quickly the item is accelerating. Any object’s velocity is determined by the rate at which its displacement changes, so its starting and ending positions are crucial.

Frequently Asked Questions

1.What is the Initial and Final Velocity?

Ans: An object’s initial velocity is its speed at time zero, or when it first begins moving, and its final velocity is its speed when the journey has come to an end.

2. State the difference and Similarity between Speed and Velocity.

Ans: The pace at which a distance changes is known as an object’s speed, whereas the rate at which its displacement changes is known as its velocity. Speed and velocity are scalars and vector quantities because distance and displacement are, respectively, scalar and vector quantities. Since both distance and displacement are expressed in meters, there is an m/s correspondence between speed and velocity.

3. What are the differences between Velocity and Acceleration?

Attributes	Velocity	Acceleration
Definition	The speed of an object in a given direction.	Acceleration implies any change in the velocity of the object with respect to time.
Calculated with	Displacement.	Velocity
What is it?	Rate of change of displacement.	Rate of change of velocity.
Formula	Displacement/Time	Velocity/Time
Unit of Measurement	Meter/Second	Meter/second²

4. What do Velocity Time Graphs Show?

Ans: A velocity-time graph displays the sprinter’s object’s changing speed, as well as the speed of any other moving item or person. The slope of the graph line on a velocity-time graph is used to illustrate acceleration. If the line slopes downhill, as it does between 7 and 10 seconds, then acceleration is negative, and velocity is dropping.