Introduction
Electric charge is an intrinsic property of matter that allows it to experience a force when placed in an electric field. Charges are classified into two types or signs: positive, and negative. You can create a simple charged object by rubbing a balloon against your hair, which transfers charges from one body to another. This is what gives rise to static electricity, so named because there is no “flow” of charges here. You can do the same with carpets and other woollen items. In this article, we will discuss electric charges in detail.
Electric Charge Definition
Electric charge is a natural property of matter that allows it to experience a force when placed in an electric or magnetic field. It is a scalar quantity with no direction but it is classified into positive and negative types.
Typically, charges are created via the transfer of electrons and the body that donates electrons is said to be positively charged, while the one that receives it becomes negatively charged. Just like magnets, like charges repel each other and opposite charges attract. Electrons are present in the atoms of every single element and thus, atoms are neutral as a whole, meaning that they carry no net charge. However, objects can gain charge via the transfer of electrons. Mathematically, the charge on an electron is equal to \(\;{\bf{1}}.{\bf{6}} \times {\bf{1}}{{\bf{0}}^{ – {\bf{19}}}}{\bf{C}}\). Further, charge is always transferred as an integral multiple of this quantity. That is, the charge on any object must be:
Q=ne
Q=total charge
e= charge on electron
n= number of electron
Basic properties of electric charge
Conservation of electric charge: Just like mass and energy always remain conserved in nature, electric charge is also a fundamental quantity that can never be created or destroyed. Rather, it is only transferred from body to body.
Example: Let us assume we have 15 C of charge on an object. We can redistribute it across several objects in any way we want, but we cannot make this charge vanish into nothingness.
Additive nature of electric charges: Since charges are scalar quantities, multiple charges on a system can be added algebraically.
For a system containing n number of charges \({q_1},{q_2},{q_3},…………{q_n}\), the total charge would be
\(Q = {q_1} + {q_2} + {q_3} + …………{q_n}\)
Note that if some of the charges are negative, that sign must be taken into account.
Quantization of electric charge: Since charge is always transferred as an integral multiple of the charge on one electron (represented by e), the total charge on any system is always quantized in units of e.
Q=ne
Transfer of charges: Charged bodies, when brought in contact, can exchange charges. That is, charge can flow across materials in contact in order for there to be equilibrium.
Like charges repel: Like charges repel each other. This fundamental property of charges is an essential force that keeps the universe stable and without it, nothing in this world would exist.
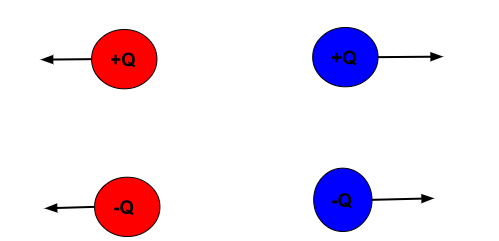
Like charges repel
Unlike charges attract: Just like magnets, unlike charges attract. This is what allows electrons to remain in orbit and thus, anything in this world to exist.
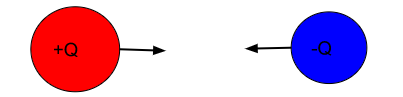
Linkage with mass: Charges cannot exist nowhere and must be present on some body.
Charge is invariant: Regardless of how fast a body moves and what frame of reference its speed is measured in, the charge on it remains the same.
Electromagnetic properties: Charges at rest produce an electric field and those in motion, produce a magnetic field. When charges are accelerated, they produce an electromagnetic field and give rise to electromagnetic radiation.
The Unit of Electric charge
The SI unit of the electric charge is coulomb, which is denoted by C, and in the CGS unit, it is measured in electrostat unit.
\(1C = \;3 \times {\bf{1}}{{\bf{0}}^{\bf{9}}}{\bf{C}}\)
Electric charge and field
When placed in an electric field, all electric charges experience a force, whose magnitude is given by the following relation:
F=qE
The sign of the charge and the direction of the electric field together decide the direction of this force. Note that E here represents the value of electric field and q is the charge placed inside it. For positive charges, the force is along the direction of the electric field and for negative ones, it is opposite. Note that this also allows us to define electric field as the force experienced per unit charge with SI units of N/C. That is,
\(E = \frac{F}{q}\)
Summary
This article described the concept of electric charge along with its properties and units. Electric charge is an inherent property of matter that allows bodies to experience a force in the presence of a magnetic field. Charges themselves are attracted to unlike charges and repel like ones. This property of charge is what keeps the universe stable.
Frequently Asked Questions
1. How can we generate charged bodies?
We can generate charged bodies via friction, induction, or by conduction.
2. Write down the dimensional formula of the electric charge.
As such, charge has no inherent dimensions. Instead, the formula of current allows us to write its dimensions.
\(Q = I \times t\)
Thus, the dimensions of charge are \(\left[ {{M^0}{L^0}{T^1}{A^1}} \right]\).
3. Give examples of positive, negative, and neutral bodies.
Atoms yield the best example here. All electrons inside them are negatively charged, while the protons are positively charged. However, the neutrons carry no charge and thus are neutral.
4. Write down the practical unit of charges.
Practically, a common unit of charge used is Ampere hour.
1 Amp hr = 3600 C
5. Write the definition of electric field
The electric field is a property by virtue of which, a charged object can exert electric field on other charged objects in its vicinity. It is defined as the force per unit charge.





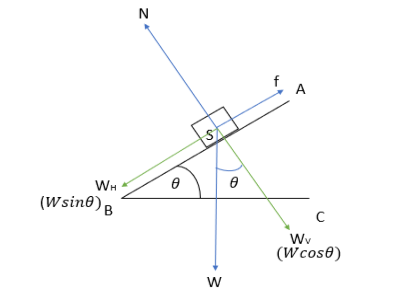
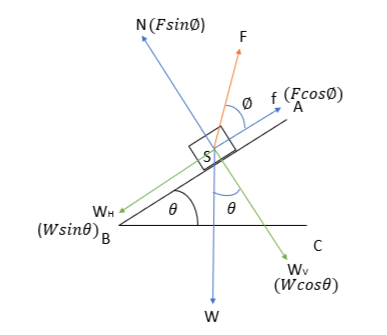
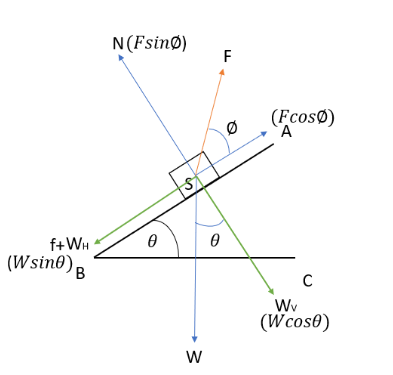
 Inclined plane AB
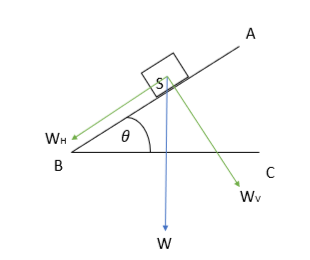
Inclined plane AB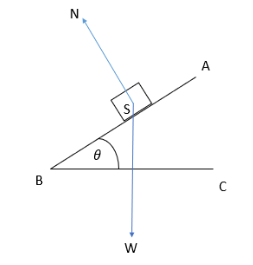
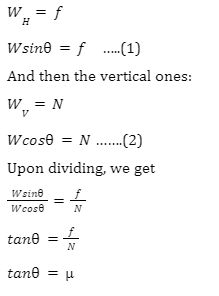





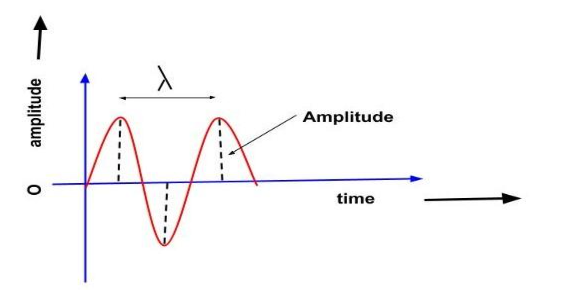
 2. Are pitch and frequency different?
2. Are pitch and frequency different?