Category: Mathematics

Introduction

A straight line that intersects another straight line at a 90-degree angle is said to be perpendicular to the first line. The small square in the middle of two perpendicular lines in the figure represents 90 degrees, also known as a right angle. Here, two lines cross at a right angle, indicating that they are perpendicular to one another.

In contrast to sloping or horizontal lines or surfaces, perpendicular lines or surfaces point directly upward. An object is at a 90-degree angle to another if it is perpendicular to it. A pair of lines, vectors, planes, or other objects are said to be perpendicular if they intersect at a right angle. Two vectors are perpendicular if their dot product equals zero.

Perpendiculars

When two lines intersect at a right angle, they are said to be perpendicular to one another. A first line is perpendicular to a second line, more specifically, if the two lines intersect and the straight angle on one side of the first line is split into two congruent angles by the second line at the intersection. Since perpendicularity is symmetric, if one line is perpendicular to another, the other line is also perpendicular to the first. As a result, we don’t need to specify an order when referring to two lines as perpendicular (to one another).

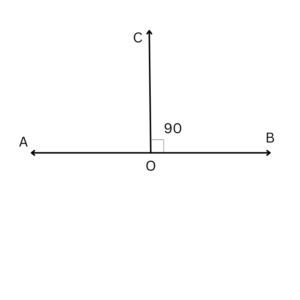
Perpendicular Lines

Segments and rays are easily extended by perpendicularity. If a line segment AB and a line segment CD result in an infinite line when both directions are extended, then the two resulting lines are perpendicular in the sense mentioned above. Line segment AB is perpendicular to line segment CD and can be represented by the symbol AB ⊥ CD. If a line crosses every other line in a plane, it is said to be perpendicular to the plane. The definition of line perpendicularity is necessary for understanding this definition.

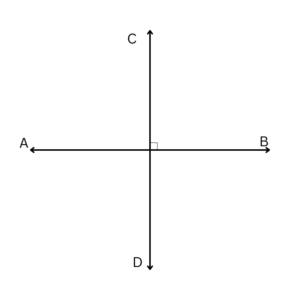
Perpendicular Theorem

According to the perpendicular line theorem, two straight lines are perpendicular to one another if they intersect at a point and create a pair of equal linear angles.

Assume two lines AB and CD intersect each other at O, such that ∠AOC = ∠COB, also since AB is a line, ∠AOC and ∠COB also form a linear pair.

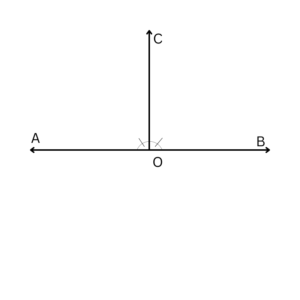
Then, ∠AOC + ∠COB = 180°

Using ∠COB = ∠AOC

⇒ ∠AOC + ∠AOC = 180°

⇒ 2 ∠AOC = 180°

⇒ ∠AOC = 90°

Thus, since the angle of intersection is 90°, we can say that AB is perpendicular to CD and vice versa.

Also Read: Related Angles

Perpendicularity: Slope Formula

Perpendicularity is known as the mathematical condition that two lines need to satisfy to be called perpendicular. Mathematically, if two lines are perpendicular to each other, then the product of their slopes is negative unity.

For example, let two lines of slope . Then these lines are said to be perpendiculars to one another if their slopes have a product -1, i.e.,  

Equation of a Perpendicular Line.

Using the conditions from previous sections, we can find the equation of the perpendicular line to any given line’s equation, at a certain point.

Let, ax + by = c be a line, and we need to find a line perpendicular to it passing through

First, we will find the slope of the given line, 

Slope of a line m = -a/b

Now, using perpendicularity, if the slope of the second line is m’, then for these lines to be perpendicular

m × m’=- 1

⇒ m’ =- 1/m =- 1/-a/b = b/a

Thus, the slope of the perpendicular line is, 

m’= b/a

Then, we have a point as well as the slope for the equation of the perpendicular line,

Using point-slope form

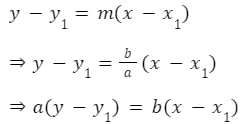
If we know the exact values of a, b and then we can further simplify this equation.

Interesting Facts about Perpendicular Lines

• In order to obtain the maximum support for the roof, walls and pillars are constructed perpendicular to the ground in our homes and other buildings. This is just one example of how perpendiculars are used in everyday life.
• Perpendiculars of two lines that meet at an angle will also meet at that same angle.

Solved Examples

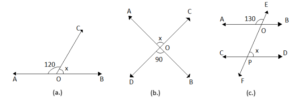
Example: Which of the following pair of lines are perpendicular, parallel, or simply intersecting?

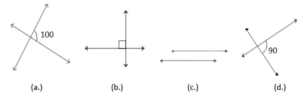
1. Intersecting, since the angle of intersection here is given to be 100 degrees.
2. Perpendicular, as we know the right angle is also represented by a small square, we can say that these lines are perpendicular to each other.
3. Parallel lines, clearly extending these lines to infinity we will never see them intersecting; thus, they are parallel.
4. Perpendicular, clearly the angle of intersection here is given to be 90 degrees.

Summary

The subject of perpendiculars and the perpendicularity of lines were covered in this article. The reader should be able to comprehend the meaning of perpendicular lines, the symbol used to represent them, as well as the formula and theorems relating to perpendicular lines, after carefully reading this article. Two lines are said to be perpendicular if their angle of intersection is a right angle. The slopes of perpendicular lines are negative reciprocals of each other.

Frequently Asked Questions (FAQs)

1.What are Perpendicular Lines?

Ans. When two lines intersect at an angle of 90 degrees, the lines are said to be perpendicular to each other.

2. How do you Find the Slope of a line Perpendicular to a Given Line?

Ans. The slope of perpendicular lines are negative reciprocals of each other; thus, the slope of a perpendicular line can be found simply by negating the reciprocal of the slope of the given line.

3. What are Perpendicular Bisectors?

Ans. A line that divides another line segment into two halves while also being at a right angle to it is known as the perpendicular bisector of the line segment.

4. Are all Intersecting Lines Perpendicular?

Ans. No, all intersecting lines are not perpendicular, but all perpendicular lines are intersecting, that too at a specific angle, i.e., 90 degree.

Also read: Properties, Area of Right-Angled Triangles

Introduction

An expression made up of variables, constants, coefficients, and mathematical operations like addition, subtraction, etc. is known as an algebraic expression. A variable is a symbol without a predetermined value. In an algebraic expression, a symbol with a fixed numerical value is referred to as the constant. A term is either a variable, a constant, or both combined through mathematical operations. A coefficient is a quantity that has been multiplied by a variable and is constant throughout the entire problem. Algebraic expressions have many uses, including representing real-world issues as well as solving various and complex mathematical equations to determine revenue, cost, etc.

Algebraic Expressions

An expression made up of variables, constants, coefficients, and mathematical operations like addition, subtraction, etc. is known as an algebraic expression. Algebraic expressions have many uses, including representing real-world issues and solving various and complex mathematical equations, finding revenue, cost, etc.

Based on a variety of number of terms, there are three main categories of algebraic expressions, i.e., monomial, binomial, and polynomial.

What is a Term in Algebra

A term is a group of numbers or variables that have been added, subtracted, divided, or multiplied together; a factor is a group of numbers or variables that have been multiplied; and a coefficient is a number that has been multiplied by a variable. Three terms, 9x², x, and 12, make up the expression 9x² + x + 12.

By drawing this conclusion, it is clear that an expression is made up of a number of terms, variables, factors, coefficients, and constants.

Terms of an Expression

A term can be a number, a variable, the sum of two or more variables, a number and a variable, or a product of both. A single term or a collection of terms can be used to create an algebraic expression. For instance, 2x and 5y are the two terms in the expression 2x + 5y.

A mathematical expression has one or more terms. A term in an expression can be a constant, a variable, the product of two variables (xy) or more (xyz), or the product of a variable and a constant (2x), among other things.

Different types of terms in an Algebraic Expression

There are different types of terms in algebraic expressions, 

Variables

These types of terms are usually represented by a symbol (most commonly its English alphabets), like x, y, z, a, b, etc. these symbols are there to represent unknown arbitrary values, hence the name ‘variables’ (since their values can vary).

Coefficient

These are not a type of a term but rather a part of a term that contains variables, coefficients are the numbers that are in multiplication with variables.

Constants

These terms are the numbers separate from the variables, and as the name suggest, they are a constant number, i.e., they are fix and never change unless they are under an operation with another constant term.

Also Read: Like and Unlike Terms

Algebraic Expressions Based on Number of Terms

A single term or a number of terms can be used to create an algebraic expression. Based on the number of terms, there are various types of expressions. These are listed below:

• Monomial Expressions: – An algebraic expression in which an expression has only one term is known as a monomial. For example, 3x, xyz, x²
• Binomial Expression: – An algebraic expression in which an expression has two terms is known as a monomial. For example, 5x + 8, xyz + x³
• Polynomial Expression: – An expression in which an expression has more than two-term within a variable is known as a polynomial. For example, 2x + 4y + 7z, x² + 5x + 3

Factors of terms: Identifying Factors

Factorization of terms refer to an algebraic expression that is written as a multiple of variables and constants.

We will now determine the factors of the terms in the given expression. To do this, we must first separate the terms and then look for their multiples. The results of this process are the factors of the given expression.

Let the expression be,

3xy + 5z²

Then the terms are,

3xy, 5z²

And the factorization of the terms are,

3 × 𝑥 × y and 5 × z × z

Solved Examples

Example 1: Identify the different terms, variables and coefficients in the following expressions

a. x² + 3xy

b. 2ab + 5c²

Solution: 

a. Expression: x² + 3xy

Terms: x², 3xy

Variables: x, y

Coefficients: 1 for x², 3 for xy

b. Expression: 2ab + 5c²

Terms: 2ab, 5c²

Variables: a, b, c

Coefficients: 2 for ab, 5 for c²

Summary

An expression made up of variables, constants, coefficients, and mathematical operations like addition, subtraction, etc. is known as an algebraic expression. Coefficients, constants, and variables are a few of the key words in the context of algebraic expressions. Similar terms are those in algebraic expressions that are constants or involve similar variables raised to similar exponents. In algebraic expressions, unlike terms are those terms that do not share the same variables or that share the same variables but have different exponents. Algebraic expressions are all polynomials, but not all algebraic expressions are polynomials. Polynomials are algebraic expressions without fractional or non-negative exponents. Algebraic expressions include fundamental identities that are used in the subject.

FAQs

1.What are Polynomials?

Ans. Polynomials are algebraic expressions with more than 2 terms and the variables have non-negative integer exponents.

2.What is a Quadratic Equation?

Ans. A quadratic equation is a polynomial equation, with maximum exponent on a variable being 2.

3. What is a term in an Algebraic Expression?

Ans. A term can be a number, a variable, the sum of two or more variables, a number and a variable, or a product of both. A single term or a collection of terms can be used to create an algebraic expression.

Introduction

There are numerous quantities and measures that cannot be stated just in terms of integers. Rational numbers were crucial in expressing how such quantities were measured. These quantities included time, money, length, and weight. Some of the quantities for which the rational numbers are most frequently employed include those ones. Rational numbers are also required in trigonometry in addition to counting and measuring. The trigonometric ratios are expressed as rational numbers. Calculations based on the Pythagorean Theorem employ a specific kind of rational integer. 

Rational Number 

The rational number can be described as the ratios expressed in numbers. The term “rational” contains the word “ratio” as well. Therefore, any ratio is represented by rational numbers. These ratios may be lower than one to one or higher than one. Let’s comprehend how rational numbers should be explained. Rational numbers are defined as any number which can be expressed in the form of where a and b are coprime integers and b ≠ 0. The denominator is not equal to zero and both the numerator “a” and denominator “b” have integer values. The outcome of the division method used to simplify the rational number is in decimal form. The decimal representation of a rational number can either be non-terminating repeating decimals or terminating decimals.

How to find Rational Numbers

Verify that each given number meets the following requirements.

• The amount must be expressed as a fraction with a denominator greater than or equal to 0.
• To get the decimals, the fraction can be further decomposed.
• Positive, negative, and 0 are all included in the set of rational numbers, which is represented as a fraction. Because they may be written as a fraction, each whole number and integer is a rational number.

Types of Rational Numbers

Positive Rational Numbers

The positive rational numbers are signified as the rational numbers having positive numerators and denominators. The rational numbers  and are positive rational numbers.

Negative Rational Numbers

The negative rational numbers are signified as the rational numbers having any one of the numerators and denominators less than 0. The rational numbers  and are negative rational numbers.

Integers

The integers can be expressed as fractions having a denominator of one. Therefore, all integers are a class of rational numbers. Integers can have the forms of 0, -8, 56 etc.

You can also read our detailed article on Positive and Negative Rational Numbers.

Terminating Decimals

The decimals are the outcome of simplifying rational numbers. Some values following the decimal point may be where these decimals end. Terminating decimals are the name given to these rational numbers. For example: 0.235, 0.056, etc.

Non-Terminating Repeating Decimals are one Type of Rational Number.

Any rational integer is a non-terminating repeating decimal if, after simplification, the outcome is a decimal with repeating digits after the decimal point. A single digit or a group of digits can be one of the recurring values. For example: 0.5533, 0,222, 0.659659, etc.

Summary

Rational numbers are the numbers that can be written in the form of a fraction, where numerator and denominator are integers. The rational numbers are represented in the form of p/q where,q the denominator is not equal to 0.  Five separate categories of rational numbers exist. Both the numerator and the denominator are bigger than zero with positive rational numbers. Any numerator or denominator of a negative rational number is less than zero. Rational numbers that have a denominator of 1 are known as integers. The rational numbers also include recurring decimals that do not terminate.

Practice Solved Example

Example: The decimal expansions of some real numbers are given below. In each case, decide whether they are rational or not. If they are rational, write in the form of p/q. 

a. 0.140140014000140000…    

We have, 0.140140014000140000… It is a non-terminating and non-repeating. So, it is irrational. It cannot be written in the form of P/q.

b.

We have,    a non-terminating but repeating decimal expansion. So, it is Rational.

Let x =

Then, x = 0.1616 ——–1

100x = 16.1616 —-2

On subtracting 1 from 2 we get,

100x – x = 16.1616-0.1616

99x = 16

x =

Frequently Asked Questions

1.The number of Rational numbers between 25 and 26 is Finite. State the give statement is True or False.

Ans: False, any two rational numbers can be integrated by an infinite number of other rational numbers. Therefore, there are infinite rational numbers between 21 and 26.

2. Why does the Rational Number not have a 0 as its Denominator?

Ans: The outcome is not a defined value if the denominator of the rational number is 0. As a result, the rational number’s denominator never equals 0.

3. Can a Rational Number have a Numerator and Denominator of Zero?

Ans: No, the numerator may equal 0. However, for every rational number, the denominator can never be 0.

4. Which Technique is used to Transform a Rational number’s Standard form to Decimals?

Ans: The standard form of a rational number is converted to decimals using the division method.

Introduction

Natural numbers, their additive inverses, and zero are all collectively known as a set of Integers. We get a whole number when we subtract a small number from a larger number. However, there are no whole numbers that can represent the difference between a large number and a smaller number, such as 12 – 37. We created integers to describe such differences. Integer Addition follows all the rules of algebra, whereas Integer Subtraction doesn’t.

Addition and Subtraction of Integers

In addition, and subtraction of integers, we will learn how to add and subtract integers with the same and different signs. Certain rules must be followed when performing operations on integers.

When you add two positive integers, you get a positive integer, but when you add two negative integers, you get a negative integer sum. Adding two different signed integers, on the other hand, results in subtraction only, with the result having the same sign as the larger number. For example,

Addition with the same sign

3 + 5 = 8 or (- 7) + (- 5) =- 12

Addition with a different sign

6 + (- 4) = 2 or (- 6) + 4 =- 2

As for subtraction, when you subtract the integers, you add the additive inverse of the second integer, i.e., you can simply just change the sign of the second integer and add the two numbers using the rules of addition. For example,

7 – 5 = 7 + (- 5) = 2

9 – (- 2) = 9 + 2 = 11

(- 3) – (- 5) = (- 3) + 5 = 2

(- 6) – 7 = (- 6) + (- 7) =- 13

Properties of Integer Addition and Subtraction

Integers have a few properties that govern how they operate. These principles or properties can be used to solve a wide range of equations. Integers are any positive or negative numbers, including zero, to refresh your memory. These integers’ properties will aid in quickly simplifying and answering a series of integer operations.

All addition, subtraction, multiplication, and division properties and identities apply to all integers. The set of positive, zero, and negative numbers represented by the letter Z is known as the set of integers. Integers have the following five operational properties:

• Closure Property
• Commutative Property
• Associative Property
• Distributive Property
• Identity Property

Closure Property

According to the closure property, the set of all integers is closed under addition and multiplication, i.e., the addition or multiplication of any two integers will always result in an integer. Subtraction of integers also follows the closure property; division however does not follow the same rule for integers. For example, 2 divided by 5 is not an integer.

If a and b are two integers, then if,

c = a + b and d = a × b

Then both c and d are also integers

Changing b with – b,

e = a – b is also an integer.

Commutative Property

According to the commutative property of addition and multiplication, the order of terms does not affect the result. Let a and b be two integers, then by the commutative law:

a + b = b + a

Also,

a × b = b × a

But subtraction and division do not follow the same rules.

Associative Property

According to the associative property of addition and multiplication, it doesn’t matter how numbers are grouped; the result is the same. Regardless of the order of the terms, parenthesis can be used.

a + (b + c) = (a + b) + c

Also,

a × (b × c) = (a × b) × c

However, again, subtraction and division are not associative for Integers.

Distributive Property

The distributive property explains how one mathematical operation can distribute over another within a bracket. To make the calculations easier, the distributive property of addition or the distributive property of subtraction could be used. In this case, integers are multiplied or divided by each number in the bracket before being added or subtracted again.

a × (b ± c) = (a × b) ± (a × c)

Identity Property

When zero is added to any integer no matter the order, the result is the same number, according to the additive identity property of integers. Zero is known as additive identity.

Let a be an integer

Then, since 0 is known as the additive identity

a + 0 = a = 0 + a

Similar to this, we have a multiplicative identity. When a number is multiplied by 1 in any order, the product is the integer itself, according to the multiplicative identity property for integers.

Again, let a be an integer,

Then, since 1 is known as the multiplicative identity

a × 1 = a = 1 × a

Again, like most other properties, subtraction and division do not follow the identity property.

Solved Examples

Example 1: Simplify the following expressions

a. (- 2) + (- 4) – 5 + 13

b. 4 × 27 + 4 × 31 – 4 × 53

Solution:

a. (- 2) + (- 4) – 5 + 13

First, we will use parentheses to separate different operations

⇒ ((- 2) + (- 4) – 5) + 13

Here we have separated the only positive term, but we still have 3 terms in the parentheses,

⇒ (((- 2) + (- 4)) – 5) +13

Now solving the operations in the parentheses one by one,

⇒ ((- 6) – 5) + 13

⇒ (- 11) + 13

⇒ 2

b. 4 × 27 + 4 × 31 – 4 × 53

First, we can see that 4 is a common factor in all the products. So we will factor it out,

⇒4 × (27 + 31 – 53)

Now we will separate the terms inside the parentheses using centric parentheses

⇒ 4 × ((27 + 31) – 53)

No solving the parentheses one after the other

⇒ 4 × (58 – 53)

⇒ 4 × 5

⇒ 20

Summary

This article gives an insight into the properties of addition and subtraction of integers. According to the addition closure property, the sum of any two integers will always be an integer. According to the subtraction closure property, the sum of, or the difference between, any two integers will always be an integer. The commutative property of integer addition states that the order of addition of integers does not matter, the result remains the same regardless. Subtraction, on the other hand, is not commutative for integers. According to the associative property of addition, the order in which numbers are grouped does not affect the outcome. The nature of integer subtraction is not associative.

Frequently Asked Questions (FAQs)

1.What are Integers? How are they different from other types of Numbers, such as Natural Numbers and whole numbers?

Ans. Integers are numbers that have no decimal value, whole values represent them. The integers contain both positive and negative numbers, along with the number 0. The positive integers are known as natural numbers, whereas the positive integers with 0, aka the non-negative integers, are known as whole numbers.

2.What are the rules for Adding Integers?

Ans. The addition of integers follows two simple rules,

1. Adding two integers of the same sign results in the addition of the value of those numbers, and the result has the same sign as the additives.
2. Adding two integers of different signs results in a difference in the value of integers, and the result has the same sign as the number with the higher value.

3.Which Properties of Integer Addition can be applied to Integer Subtraction?

Ans. The following properties of integer addition can be applied to integer subtraction,

• Closure: The closure property states that the result of the operations is in the same set as the input, i.e., subtracting two integers will always result in an integer.
• Distributive: Distributive property states that the operation of multiplication can distribute over operations such as addition or subtraction, i.e., the product of a number and a difference of two numbers is the same as the difference of the product of the two numbers with the first.

4.What is an Inverse?

Ans. The inverse of a number is another number, which, when operated under a certain operation with the original number, results in the identity of that operation. That is, for addition, the inverse is defined as the number which when added together with the original number results in 0, and for multiplication, multiplies to give 1.

Introduction

The most fundamental application of percentages is to compare two amounts while setting the second amount to 100. The use of percentages is widespread and varied aside from this. For instance, a lot of statistics in the media are expressed as percentages, including bank interest rates, retail discounts, and inflation rates. Percentages are essential for understanding the financial aspects of daily life.

The Latin word “per centum,” which means “per hundred,” is where the word “percent” originates. The task of comparing unlike fractions is very challenging. Because percentages are the numerators of fractions with a denominator of 100. Percentages have a wide range of applications in daily life, including making simple comparisons, allocating discounts in marketing, and calculating profits and losses for businesses.

Percentages

Per means “out of” in percentage, and cent means a century. In essence, the whole is always set to 100, and the relationship is between a part and the entire. The ratio known as a percentage has a denominator of 100 and the percentage symbol %.

The percentage formula is as follows:

How to find percentage from data?

To find percentage from a given data, we first need to find the fraction of the quantity from the given data. By dividing the number by a whole and multiplying the result by 100, any fraction can be expressed in percentages. Consider a society with 1000 members, 650 of whom are voters. Then the percentage of voters out of all the residents is,

% Of voters = × 100

= × 100

= 65%

Percentage of a Number

When a number is divided into 100 equal parts, the percentage of that number is the sum of those 100 parts. Calculating percentages involves multiplying the total number by the percent expressed as a fraction. For instance, let’s say we need to find 30% of 600. We can figure it out as:

30% of 600 = 600 ×  = 180

Here, 600 is total, so 30% of 600 is 180.

Applications of Percentages

One of the most useful mathematical ideas is the percentage, which has applications in practically every branch of science as well as in everyday life.

To compare fractions

Fractions can be converted to percentages to create a clear comparison representation. This is very useful when the denominators of two fractions have different values. For instance, suppose you need to compare the fractions 2/5 and 1/4. We use percentages because making a direct comparison in this situation is very difficult. For 2/5, the percentage form is 40%, and for 1/4, the percentage form is 25%. We can categorically state that 2/5 is greater than 1/4.

To estimate increment or decrement

Any change in a quantity can be expressed in terms of a percentage. For instance, a 20% decrease would occur if a person’s salary was Rs. 5000 per month one year and Rs. 4000 the following.

The formula to calculate % change in a quantity is

Change% = × 100

To calculate ‘How much’ or ‘How many’

Sometimes numbers are expressed as percentages, for example the case of a city where 40% of the people are vegan. Therefore, the percentage will enable us to determine the precise number of vegans.

The formula to calculate the number from percentage is as follows,

Quantity =  × Total

To calculate profit or loss in percentage, to mark discounts etc.

If the selling price and cost price are known, the seller can use percentages to determine its loss or profit. For instance, a seller may charge Rs. 5000 for a fan while only paying Rs. 4000. The profit margin in this case is 25%.

Solved Examples

Example: What is the discount given on an article marked Rs. 6000 with a discount of 30%.

Solution: The discount on the article is given by

Discount% = × 100

Discount = × Marked Price

Substituting values

Discount = × 6000 = Rs. 1800

A discount of Rs. 1800 is given.

Example: By what percentage is Amit’s salary, Rs. 35000, is less than from Sagar’s salary, Rs. 40000?

Solution: The difference between Amit’s and Sagar’s Salaries is

Sagar’s Salary – Amit’s Salary = 40000 – 35000 = Rs. 5000

The percentage difference between their salaries

Thus, Amit’s salary is 12.5% less than Sagar’s salary.

Summary

When portions of a quantity are given, we have seen how to convert ratios into percentages. We discussed the formula for calculating the percentage of a number. An increase or decrease in a specified quantity can also be expressed as a percentage. The profit or loss in a specific transaction can be expressed in terms of percentages.

Frequently Asked Questions

1.What is the Importance of Percentage in Sciences other than Mathematics?

Ans. Percentage plays an important role in many aspects of business science, physical science, chemical science etc. In business science (statistics in particular) percentage is used to represent the parts of a data. In physical science percentage is used in various formulae, and derivations to represent efficiency, error and other such things. In chemical science percentage is used to calculate the concentration of different chemicals and composition of solutions etc.

2.How is Percentile Different from Percentage?

Ans. The value in the distribution or level at or below which a specific percentage of the score lies is represented by the percentile. For every hundred, which is the measurement unit, is referred to as the percentage.

3.What is the Relationship between Percentage and Probability?

Ans. Probability of an event can also be expressed as a percentage. For example, if the probability of an event is x, then the percentage probability is given by

% Probability = 𝑥 x 100%

Read More: Ratio and Percentage Formula and Examples

Introduction

Pythagoras, a Greek philosopher who was born around 570 BC, is remembered by the theorem’s name. The theorem has likely been proved the most times of any mathematical theorem using a variety of techniques. The proofs are numerous, some of which go back thousands of years, and include both geometric and algebraic proofs. The Pythagorean theorem is extremely useful when determining the shortest distance between two points or the degree of the mountain slope. In a right-angle triangle the square of the hypotenuse is said to be equal to the sum of the squares of the two legs.

Right Angle Triangle

A triangle with a right angle is one in which one angle is 90 degrees. We refer to this triangle as a right-angle triangle since 90 is also referred to as the right angle. Triangle sides with a right angle were given unique names. The side directly opposite the right angle is known as the hypotenuse. Based on the values of the various sides, the right triangles are divided into isosceles and scalene types.

Properties of Right-Angle Triangle

• The height, base, and hypotenuse of a right-angle triangle are its three sides. 
• The two adjacent sides are referred to as base and height or perpendicular.
• Three similar right triangles are formed if we draw a perpendicular line from the vertex of a right angle to the hypotenuse.
• The radius of a circle whose circumference includes all three vertices is equal to one-half the length of the hypotenuse.
• The triangle is known as an isosceles right-angled triangle, where the adjacent sides to the 90° are equal in length if one of the angles is 90° and the other two angles are each equal to 45°.

Pythagoras Theorem

Pythagoras is a potent theorem that establishes the relationship between the sides of a right-angle triangle. According to Pythagoras’ theorem –

“Square of the hypotenuse is equal to the sum of the square of the other two legs of the right angle triangle”. Mathematically, it may be expressed as

              Hypotenuse² = Perpendicular² + Base² 

Area of the Right-Angle Triangle

The area of the right-angle triangle is the region enclosed within the triangle’s perimeter. The formula for a right-angle triangle’s area is.

Area of right-angle triangle = (Base × Perpendicular)

Facts

• A triangle must be a right triangle if it obeys Pythagoras’ theorem.
• The longest side of a triangle is the one that makes the largest angle.
• When the midpoint of the hypotenuse of a right-angled triangle is joined to the vertex of the right angle, the resulting line segment is half of the hypotenuse. In other words, the center of the hypotenuse is the circumcenter of the right-angled triangle.
• If two sides of a right angle are known, we can find the other side using Pythagoras’ Theorem.
• From the provided value of sides, we may determine whether a right-angle triangle is possible.

Summary

A right-angled triangle is one in which one of the angles is a right angle (90 degrees), and the hypotenuse is the side opposite to the right angle. The hypotenuse square of a right-angled triangle is equal to the sum of the squares of the other two sides, according to Pythagoras’ Theorem.

Solved Examples

Example 1: In the right-angle triangle, If PQ = 5 cm and QR = 12 cm, then what is the value of PR?

Solution:  By Pythagoras theorem, we have, 

   Hypotenuse² = Perpendicular² + Base²

PR² = 5² + 12²

PR² = 25 + 144

PR =  = 13 cm

Hence, the value of PR is 13 cm.

Example 2: If a triangle has three sides 9cm, 5 cm, and 7 am respectively, check whether the triangle is a right triangle or not.

Solution: According to the theorem, if the square of the longest side equals the sum of the squares of the other two sides, a triangle is said to be, a right triangle. 

9² = 5² + 7² 

81 = 25 + 49

81 ≠ 74

 Thus, 81 is not equal to 74. Hence, the given triangle is not a right-angle triangle.

Frequently Asked Questions

1.Which Side of a Right-Angled Triangle is the Longest?

Ans: The hypotenuse of a right-angled triangle is its longest side.

2.What is a Right-Angled Triangle’s Perimeter?

Ans: The perimeter of a triangle is the sum of all sides.

Perimeter = base + perpendicular + hypotenuse.

3.Can there be two Right Angles in a Triangle? Explain.

Ans: No, there can never be two right angles in a triangle. A triangle has exactly three sides and interior angles that add up to 180 degrees. This means that if a triangle contains two right angles, the third angle must be zero degrees, which means that the third side will overlap the opposite side. Therefore, a triangle with two right angles is not possible.

Introduction

Two lines can intersect at any point or come together at a common point to form an angle. An angle is defined as having two arms that extend outward, and its measurement is expressed in degrees. Angles in pairs are the related angles. Any pair of angles that have a specific relationship between them is therefore referred to as related angles. A specific name refers to these angles. Since the angles are related to a particular circumstance, they are known as related angles.

Related Angles

Related angles are those that have a particular relationship with one another. Each pair of connected angles is given a unique name. There is a specific standard for the associated angles.

Types of Related Angles

The related angles have specific names depending on the type of criteria. When the sum of the two angles is 90 degrees, they are said to be complementary angles. If the sum of the two angles is 180 degrees, they are said to be supplementary angles. In a plane, two angles are said to be adjacent if they share a common vertex, a common arm, and non-common arms that are on the opposite side of the common arm. Due to their shared arm, adjacent angles always lie next to their other pair. The two adjacent angles are regarded as a linear pair of angles when the sum of their respective measures equals 180 degrees. Since their non-common arms are two rays pointing in opposite directions, they are known as linear pairs of angles. When a transverse crosses parallel or non-parallel lines, various angles are created. Alternate exterior angles, alternate interior angles, vertically opposite angles, and corresponding angles are the different types of angles.

Complementary Angles

Complementary angles are those where the sum of the measures of two angles is 90 degrees.

Supplementary Angles

These angles are referred to as supplementary angles when the sum of the measures of two angles is 180 degrees.

Adjacent Angles

If two angles in a plane share a vertex, a common arm, and their non-common arms are located on opposite sides of the common arm, then the angles are said to be adjacent.

Adjacent Angles: Linear Pair

If two adjacent angles share a common vertex, a common arm, and non-common arms that are oriented in opposition to one another, they are referred to as linear pairs of angles.

Alternate Exterior Angles

The angles outside the parallel lines and on the opposing sides of a transversal that intersects parallel lines are referred to as alternate exterior angles. Every other exterior angle is equal.

Alternate Interior Angles

The angles inside the parallel lines and on the opposing sides of a transversal that intersect parallel lines are referred to as alternate interior angles. All of the interior angles alternately are equal.

Vertically Opposite Angles

The angles are formed by two lines’ intersections, which are opposite. The angles that are vertically opposite are always equal in size.

Corresponding Angles

The angels that are lying parallel to the lines and on the same side of the transversal are always equal. Corresponding angles is the name given to these angles.

Interesting Facts about Related Angles

The linear angles’ and supplementary angles’ combined measures are equal. But the specifications for each of these angles vary. The placement of the angles is what causes this. A common arm will always connect the linear pair of angles. The supplementary angles, however, don’t always follow the same pattern. As a result, while all supplementary angles are not linear pairs, all linear pairs are supplementary angles.

Solved Examples

Example: Solve for x in the following images.

Solution: 

1.This is a linear pair that lies on line AB.

∠AOC + ∠COB = 180°

120° + x = 180°

x = 180 – 120

x = 60°

1.This is a pair of vertically opposite angles

x = 90°

1.Here, we have no direct connection between a given angle and the angle measured x.

Thus, we will use corresponding angles to find ∠CPO, to use the relation between ∠CPO and x.

∠CPO = ∠AOE

∠CPO = 130°

Now, ∠CPO and ∠OPD are a linear pair on the line CD.

∠CPO + ∠OPD = 180°

130 + x = 180

x = 180 – 130

x = 50°

Summary

There are specific requirements for the related angles. There are always two of them. The angles are referred to as supplementary angles if the total of the pair of angles is 180 degrees. The complementary angle pairs also add up to 90 degrees. The angles that are next to each other are those that have a common arm and other arms that are on different sides of the common arm. Adjacent angles make up the linear pair of angles. The linear pair of angles add up to 180 degrees.

Frequently Asked Questions (FAQs)

1.What are Related Angles?

Ans. Related angles are a pair of angles that have some sort of relation in their geometric structure, which gives them a relationship mathematically using a simple equation.

2.What is the Relationship between Angles on the Same Side of Transversal?

Ans. Angles on the same side of the transversal are shown below,

These angles are supplementary to each other, i.e., the sum of these two angles is 180 degrees.

In a pair of lines and a transversal, if corresponding angles are equal. What does it say about the pair of lines?

If in a pair of lines and a transversal, if the corresponding angles are equal, the pair of lines are parallel.

3.Are all Supplementary Angles Linear Pairs?

Ans. No, all supplementary angles are not linear pairs, since by definition linear pairs are the adjacent angles whose sum is 180 degrees, but for supplementary angles, the condition of adjacent angles need not be fulfilled.

Introduction

The relationship between two expressions on either side of the equal to sign is represented by an equation in mathematics. One equal symbol and one variable are used in this kind of equation. Simple equations use arithmetic operations to balance the expressions.

A simple equation is an equation that shows the relationship between two expressions on both sides of the sign. Only one variable appears in these kinds of equations, either on the first side or the other side of the equal symbol. For instance, 83 = 5 – 4z. In the provided example, the variable is z. Simple equations use arithmetic operations to balance the expressions on both sides. Linear equations in one variable are also regarded as simple equations.

Equations

Equations are relationships between two or more expressions connected by the equals sign, or “=.” Variables, coefficients, and constants are the three components of an equation.

Variables: Variables are the names given to the symbols (typically English alphabets) that are assigned to an arbitrary, unknowable value.

Coefficients: The coefficients of a term are the numbers that are multiplied by a variable or the product of two variables in that term.

Constants: Constants are the numbers that are independent of variables.

Simple Equations

A type of equation known as a simple equation compares two linear expressions with just one variable in common. Several instances of basic/simple equations are

3x + 4 = 7

4x + 5 = 3x + 8

Since many of the situations, we encounter in real life can be formulated as simple equation problems, we can use simple equations to obtain the desired results in a variety of areas of life.

Simple Equations questions

Simple equation problems, which can be represented by a simple equation to find the value of something unknown based on some given conditions, are known as simple equation questions. One such example of applying simple equations to real-world situations is provided, 

Let’s say Amar and Bipin, two friends, are purchasing apples. Amar might have purchased 5 kg and Bipin 3 kg. If Amar paid Rs. 80 more than Bipin, we must determine the cost of a kg of apples. The following simple equation can be used to represent this situation:

5x = 3x + 80, where x is the price of 1 kg apples.

Solving Simple Equations

To answer questions involving simple equations, we change the equation so that the term with the variables is on one side of the equation and the term with constants is on the other. We then simplify both sides so that there is only one term on each side, one with variables and the other with constants.

The value of the variable is then obtained by simply multiplying the equation by the reciprocal of the coefficient.

Now, let’s look at some examples to help us better understand it.

Example: Solve the following simple equation, 5x – 20 = 3x + 60

Solution: Here we have 5x – 20 = 3x + 60

Adding 20 to both sides while subtracting 3x to move terms with variables to one side and constants to the other.

⇒ 5x – 20 + 20 – 3x = 3x + 60 + 20 – 3x

⇒ 5x – 3x = 60 + 20

⇒ 2x = 80

Dividing by 2 on both sides

⇒ x = 40

Simple Equation Problems

Simple equation problems are mathematical issues from the real world that are modelled by simple equations. We must first determine the number of arbitrary values present and their relationships to represent a given situation using a simple equation. If there is only one arbitrary value, it is easy to create a simple equation to describe it; however, if there are several arbitrary values, we must establish a direct relationship between them to do so.

Example: Determine whether the following scenario can be modelled as a simple equation or not. Amit is currently twice as older than his younger brother Sagar. The combined age of Amit and Sagar was 23, two years ago. Identify their current ages.

Solution: Since Amit’s age and Sagar’s age are arbitrary values, the only way we can depict this situation in a simple equation is if there is a direct correlation between their ages, which is implied by the first statement that Amit is currently twice as old as Sagar. As a result, we can express this as a simple equation problem.

Let Sagar’s present age be x years

And Amit’s present age be y years

Then, ATQ

In present, y = 2x

Also, two years ago, (x – 2) + (y – 2) = 23

Substituting y = 2x in the second equation,

⇒ x – 2 + 2x – 2 = 23

Equations in Everyday Life Examples

When a value for a quantity or identity is unknown in a real-world situation and cannot be determined by a simple mathematical operation, linear equations are used, such as when estimating future income, forecasting future profits, or figuring out mileage rates.

Here are a few real-world instances where applications of linear equations are used.

• Can be used to identify age-related problems.
• It is used to determine the distance, duration, and speed of a moving object.
• It is used to resolve problems involving money, percentages, etc.

Solved Examples

Example: Calculate the value of y from the equation:  – 5 = 6.

Solution: We will simplify the equation first by separating the variables and constants,

– 5 = 6

Add 5 on both sides,

⇒  – 5 + 5 = 6 + 5

⇒  = 11

Multiply by 3 on both sides,

⇒  x 3 = 11 x 3

⇒ 11y = 33

Divide by 11 on both sides,

⇒ y = 3

Summary

Simple equations are also known as linear equations when they contain multiple variables and can be resolved using a variety of techniques. To solve problems from daily life, such as how to measure an unknown length, etc., we use simple equations. The typical method of representing the relationship between variables is through simple equations. A simple equation is a linear equation that only has one variable. Simple equations were credited to Rene Descartes as their creator. One of the foundations of algebra is simple equations.

Frequently Asked Questions (FAQs)

1. What are Linear Equations?

Linear equations are the mathematical relations that relate two expressions of degree 1 with the equal to symbol.

2. What are Simple Equations?

Simple equations are linear equations that have only one variable. Simple equations can be solved easily and are very useful in many days to day life problems.

3. What are the different methods of Solving Simple Equations?

There are two ways that we can solve simple equations. The techniques are the systematic method and the trial-and-error method.

4. What is a Rational Expression?

A rational expression is expressed in terms of the fraction of two algebraic expressions, and it also belongs to the class of simple equations.

Introduction

Natural numbers, their additive inverses, and zero are all collectively known as a set of integers. We get a whole number when we subtract a small number from a larger number. However, there are no whole numbers that can represent the difference between a large number and a smaller number, such as 12 – 37. We created integers to describe such differences. Integer Addition follows all the rules of algebra, whereas integer subtraction doesn’t.

Division of Integers

We can use the properties of integer division because we are accustomed to working with whole numbers and natural numbers. 

The Division of Integers rules:

Rule 1: A positive integer is always the quotient of two positive integers or two negative integers.

Rule 2: A positive integer’s quotient when divided by a negative integer is always negative.

One important thing to keep in mind is that you should always divide without signs, but once you have the integer solution, give the sign following the sign specified in the problem.

Learn More about Properties of Division of Integers. Check out more videos in Maths Class 7 Lesson no 01.

Properties of Integer Operations

Integers have a few properties that govern how they operate. These principles or properties can be used to solve a wide range of equations. Integers are any positive or negative number, including zero, to refresh your memory. These integers’ properties will aid in quickly simplifying and answering a series of integer operations.

All addition, subtraction, multiplication, and division properties and identities apply to all integers. The set of positive, zero, and negative numbers represented by the letter Z is known as an integer. Integers have the following five operational properties:

• Closure Property
• Commutative Property
• Associative Property
• Distributive Property
• Identity Property

Closure Property

According to the closure property, the set of all integers is closed under addition and multiplication, i.e., addition or multiplication of any two integers will always result in an integer. Subtraction of integers also follows the closure property; division however does not follow the same rule for integers.

If a and b are two integers, then if,

c = a + b and d = a × b

Then both c and d are also integers.

But r = a/b is not always an integer.

Thus, the division of integers is not always closed.

Commutative Property

According to the commutative property of addition and multiplication, the order of terms does not affect the result. Let a and b be two integers, then by the commutative law:

a + b = b + a

Also,

a x b = b x a

But subtraction and Division do not follow the same rules.

Associative Property

According to the associative property of addition and multiplication, it doesn’t matter how numbers are grouped; the result is the same. Regardless of the order of the terms, parenthesis can be used.

a + (b + c) = (a + b) + c

Also,

a × (b × c) = (a × b) × c

However, again subtraction and Division are not associative for Integers.

Distributive Property

The distributive property explains how one mathematical operation can distribute over another within a bracket. To make the calculations easier, the distributive property of addition or the distributive property of subtraction could be used. In this case, integers are multiplied or divided by each number in the bracket before being added or subtracted again.

Multiplication is distributive from both sides, but Division is distributive only from the right side (denominator/divisor)

(a ± b) ÷ c = (a ÷ c) ± (b ÷ c)

Identity Property

When any integer is added to zero no matter the order, the result is the same number, according to the additive identity property of integers. Zero is known as additive identity.

Let a be an integer

Then, since 0 is known as additive identity

a + 0 = a = 0 + a

Similar to this, we have the multiplicative identity. When a number is multiplied by 1 in any order, the product is the integer itself, according to the multiplicative identity property for integers.

Again, let a be an integer,

Then, since 1 is known as the multiplicative identity

a × 1 = a = 1 × a

Again, like most other properties, subtraction and division do not follow the identity property.

BODMAS Rule

To simplify the calculations of more than two numbers having several types of operators, we have formed a rule that governs how to put parentheses around certain terms when solving the parentheses from the centre simplifies the calculation a lot.

This rule goes like

Bracket Of Division Multiplication Addition Subtraction – BODMAS

Here in this definition the ‘Of’ stands for functions such as exponents or square roots. So according to this rule, we put the centre of parentheses or brackets on subtraction, then addition, then multiplication and then division leaving the functions outside.

Solved Examples

Example: Are the following Integer operations closed (have an Integer result)?

a.  2 + 3/ (5 – 2)

b.  4(3/8) + 5/15

Solution:

a.  2 + 3/ (5 – 2)

Using BODMAS, we will simplify the terms by solving within the parentheses first.

⇒ 2 + 3/ (3)

⇒ 2 + 1 = 3

This operation is closed.

b.  4(3/8) + 5/15

Using BODMAS, we will simplify the terms by solving within the parentheses first.

This operation is not closed.

Also Read: Properties of Addition and Subtraction of Integers

Summary

This article discusses the topic of Integers, Integer Division. While also shining a light on the properties of Integers operations such as closure property, commutative property, etc. Integer division however does not follow most of these properties.

FAQs

 1. What are Integers? How are they different from other types of numbers, such as natural numbers and whole numbers?
Ans. Integers are numbers that have no decimal value, they are represented by whole values. The integers contain both positive and negative numbers along with the number 0. The positive integers are known as natural numbers, whereas the positive integers with 0, aka the non-negative integers, are known as whole numbers.

2. What are the rules for Dividing Integers?
Ans. The division of integers follows two simple rules,

1. Dividing two integers of the same sign results in the quotient of the value of those numbers and the result has a positive sign.
2. Dividing two integers of different signs results in the quotient of the value of integers and the result has a negative sign.

3. Which is the only Property of Integer Operations that Division follows, and on What Condition?
Ans. The distributive property is the only property of integer operations that the division of integers follows, and it follows the distributive property only from the right-hand side.

Introduction

Although factors and multiples are entirely different concepts, they are related. To determine the factors, we divide the given number by another number, whereas multiples of the given number can be obtained by multiplying the given number by any other number. Multiplication is involved in both ideas. To obtain a given number, we multiply two numbers; the two numbers we multiplied are referred to as the obtained number’s factors.

For example, 4 x 5 = 20. Therefore, 20 is a multiple of 4 and 5, and 4 and 5 are factors of 20.

The number that is the factor of two or more numbers is referred to as the common factor. GCD (Greatest Common Divisor) and HCF (Highest Common Factor) are terms that relate to this idea.

The common multiple is the number that is a multiple of two or more other numbers. The Least Common Multiple, or LCM, is related to this idea. Different divisibility criteria can be used to determine whether a given number is divisible by another without actually conducting the division operation.

Factors

A number must divide completely, leaving no remainder, to be the factor of any other number. In other words, we can also say that the divisor is a factor of the dividend if a number (the dividend) is exactly divisible by any other number (the divisor), leaving no remainder.

For Example: Let’s take the number 36, if we check for factors of 36, we have

36 = 1 x 36 = 2 x 18 = 3 x 12 = 4 x 9 = 6 x 6

Properties of Factors

• If a division of a number by another number leaves no remainder, then that second number is said to be the factor of the first number.
• A number can only have a finite number of factors.
• Prime numbers are those that only have themselves and the number 1 as factors.
• Composite numbers are those that have more than two factors.
• Finding a number’s factors involves using division.
• The obtained factors are always less than the initial number.

Multiples

Multiples are numbers created by multiplying the given number by integers. The multiplication table shows the multiples of a given number.

Properties of Multiples

• The results of multiplying an integer by a given number are referred to as the given number’s multiples.
• There are an infinite number of multiples of a number.
• Finding a number’s multiples requires the use of multiplication.
• The multiples of a given number exceed or are equal to that number.
• Every number is a multiple of itself.

Difference between Factors and Multiples

Some differences between factors and multiples are given in the table below:

Factors	Multiples
Factors are exact divisors of a number.	Multiple has the number as its exact divisor.
Factors of a number are finite.	Multiples of a number are infinite.
Factors are obtained by division.	Multiples are obtained by multiplication.
Factors of a number are always less than or equal to the number itself.	Multiples of a number are always greater than or equal to the number itself.

Common Factors and HCF

A common factor is any factor that two or more numbers share.

For example, take 35 and 42

Factors of 35 = 1, 5, 7, 35

Factors of 42 = 1, 2, 3, 6, 7, 14, 21, 42

Both 35 and 42 have some factors such as 1 and 7 that are common to both, these are known as common factors of 35 and 42.

Now, in this case in the list of common factors, 7 is the largest number, or we can also call it the highest common factor, i.e., HCF.

Thus, HCF or the highest common factor of a set of numbers is defined as the largest number that divides all the numbers in the given set of numbers.

Common Multiples and LCM.

Common multiples are those multiples that are shared by two or more different numbers.

For example, take 6 and 8

Some multiples of 6 are, 6, 12, 18, 24, 30, 36, 42, 48, 54, 60 etc.

Some multiples of 8 are 8, 16, 24, 32, 40, 48, 56, 64, 72, 80 etc.

Here, both 6 and 8 share some common multiples such as 24, 48 and infinitely many more. These are known as common multiples of 6 and 8.

In this case, in the list of common multiples, 24 is the smallest, or we can also call it the least common multiple, i.e., LCM.

Thus, LCM or least common multiple of a set of numbers is defined as the smallest number that is a multiple of or is divisible by all the numbers in the given set of numbers.

Solved Examples

Question: Find the list of factors of 36.

Solution: We know that 1 and the number itself, i.e., 36, are the two trivial factors, so we will start dividing by the next number.

36 ÷ 2 = 18, Thus, 2 and 18 are two more factors of 36, moving to the next number

36 ÷ 3 = 12, Thus, 3 and 12 are two more factors of 36, moving to the next number

36 ÷ 4 = 9, Thus, 4 and 9 are two more factors of 36, moving to the next number

Clearly, 36 is not divisible by 5 since it doesn’t have 5 or 0 in the unit place, moving to the next number

36 ÷ 6 = 6, Thus, 6 is the final factor of 36.

Factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18, and 36.

Summary

This article provides insight into the topic of Factors and Multiples, while also shining a light on the concept of common factors and common multiples. To completely divide another number without leaving any remainder, a number must be the factor of that other number. The multiples are the results of multiplying the given number by integers. Common multiples are those multiples that are shared by two or more different numbers. A common factor exists for two or more different numbers.

Frequently Asked Questions (FAQs)

1. What are Factors and Multiples?

Ans. Factors of a number are defined as the number that divides the given number completely and evenly without leaving any remainder.

Multiples on the other hand are the numbers obtained by multiplying the given number by different integers.

2. What are Prime Numbers?

Ans. Prime numbers are defined as numbers greater than 1 that have only 2 factors, i.e., 1 and the number itself. Some examples of prime numbers are 2, 3, 5, 7, 11, etc.

3. What is the Fundamental Theorem of Arithmetic?

Ans. The fundamental theorem of arithmetic states that every number can be broken into the product of some prime numbers, also known as its prime factors. This product is unique to a number and cannot ever change no matter how you find it, only the order of the product changes.

4. What is the Relationship between HCF and LCM of two Numbers?

Ans. The relationship between is defined as: The product of HCF and LCM of two numbers is equal to the product of the two numbers.

HCF (a, b) × LCM (a, b) = a × b