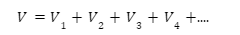Category: Mathematics

Introduction

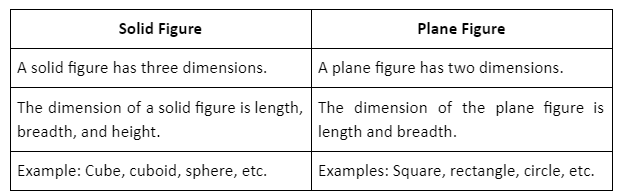
Three-dimensional (3D) shapes are solids with three dimensions: length, breadth (width), and height. The word “3D shapes” refers to three dimensions. Every 3D geometric shape takes a certain amount of space depending on its dimensions, and in daily life, we are surrounded by many 3D shapes. Cubes, cuboid forms, cones, and cylinders are a few examples of 3D shapes.

3D shape example

There are several three-dimensional (3D) shapes with various bases, volumes, and surface areas. Let’s talk about each one individually.

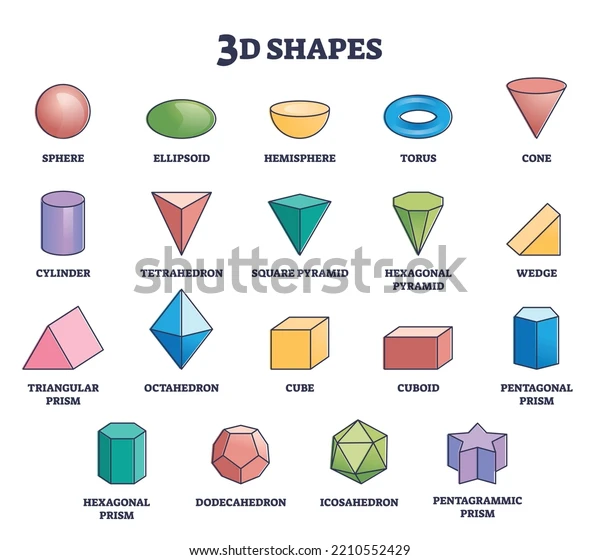
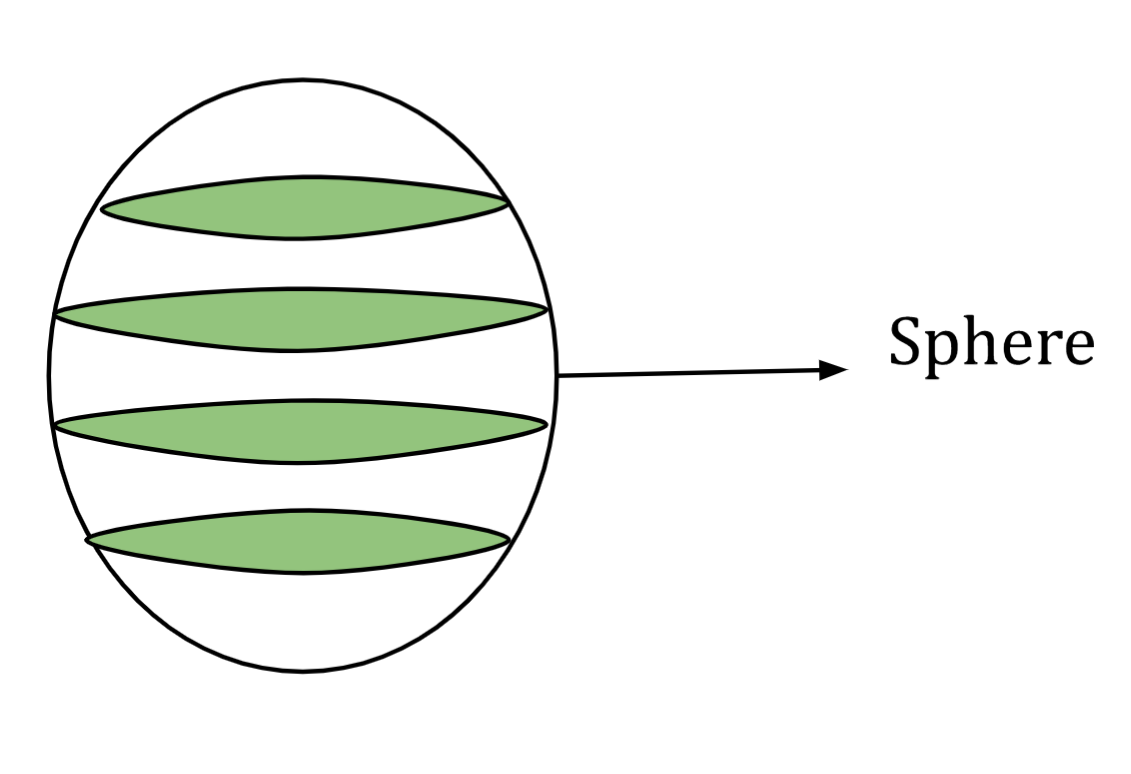
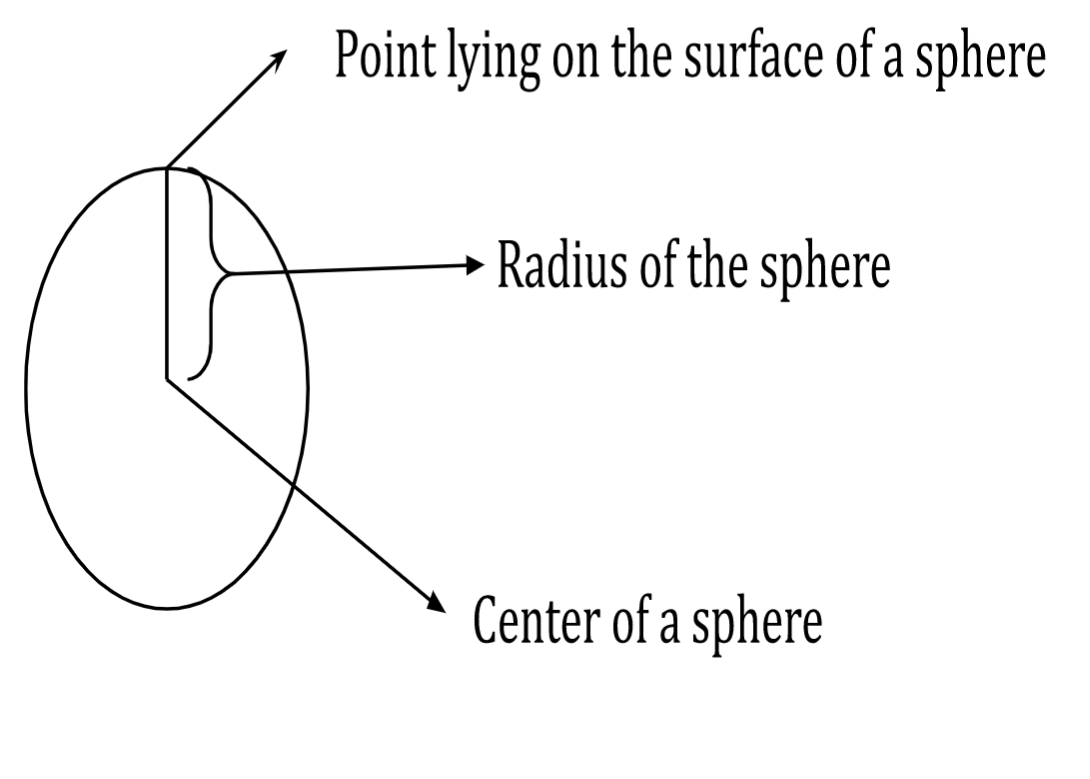
Sphere

A sphere has a round shape. It is a 3D geometric shape with equidistant points from its centre at every point on its surface. Though it resembles a spherical, our planet Earth is not one. Our planet has a spheroid form. Although a spheroid resembles a sphere, it differs in radius from the centre to the surface at different points. 
Also read : how to calculate volume of a sphere

Cube and cuboid

The three-dimensional (3D) shapes cube and cuboid share the same number of faces, vertices, and edges. The primary distinction between a cube and a cuboid is that a cube has six square faces, whereas a cuboid has six rectangle faces. The volume and surface area of a cube and a cuboid are different. A cube has the same length, breadth, and height, whereas a cuboid has varied length, width, and height.

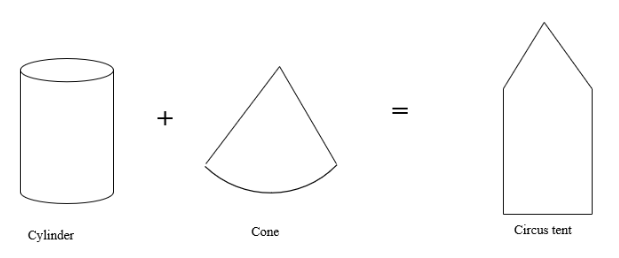
Cylinder

A cylinder is a 3D form that has one curved surface, two circular faces—one on top and one on bottom—and two round faces. There is a height and a radius to a cylinder. The perpendicular distance between the top and bottom faces of a cylinder is its height. 

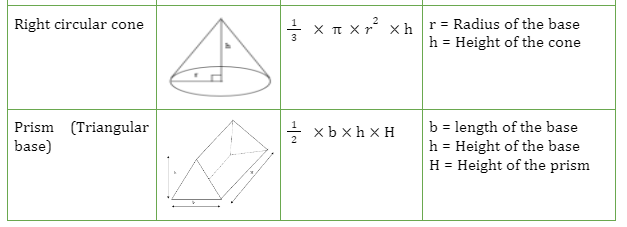
Cone

Another three-dimensional shape is the cone, which has a flat base (of circular shape) and a pointed apex. The cone’s top, pointed end is referred to as the “Apex.” A cone’s surface is also curved. Similar to a cylinder, a cone can be divided into two types: an oblique cone and a right circular cone.

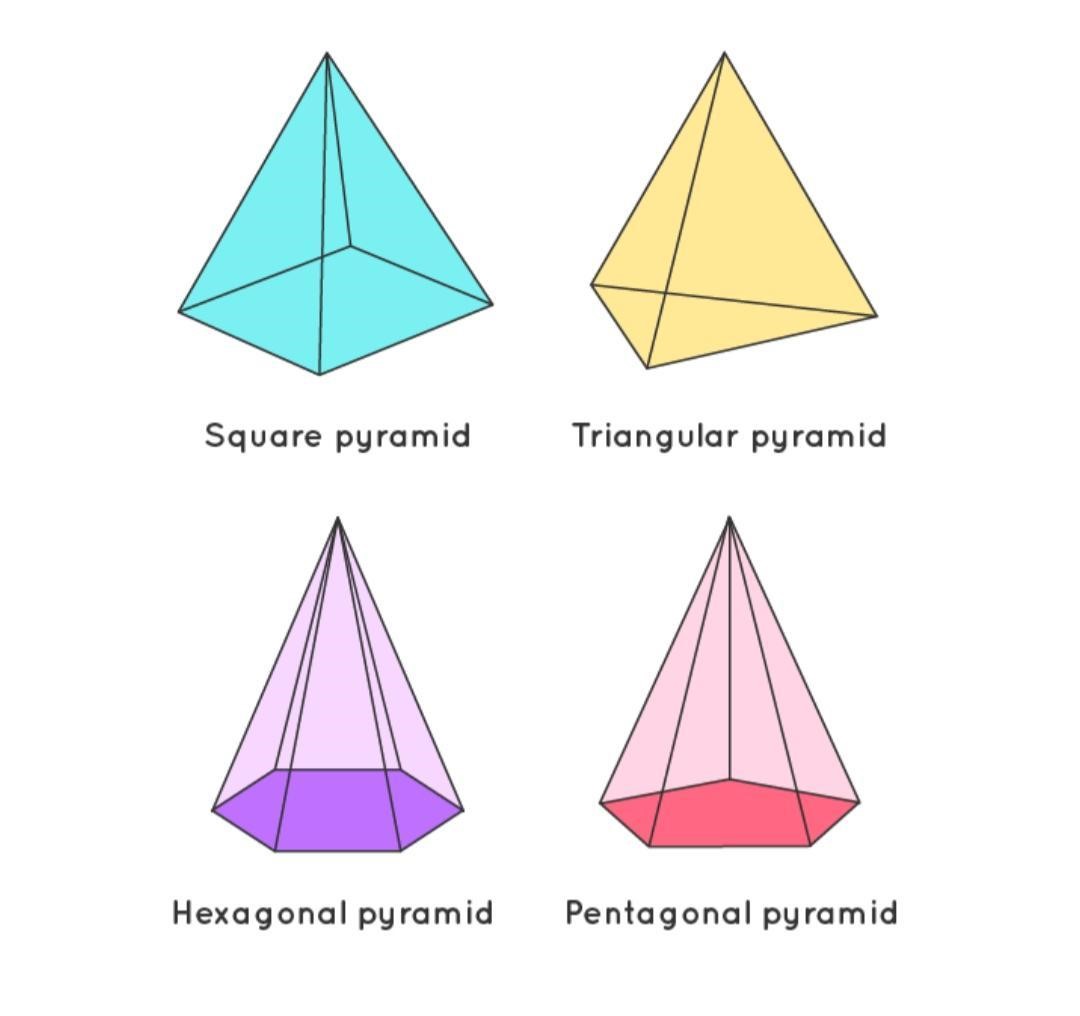
Pyramid

A pyramid is a polyhedron with a flat-faced, straight-edged base and an apex. They can be divided into regular and oblique pyramids depending on how closely their apex aligns with the middle of the base.

• Tetrahedron is the name given to a pyramid having a triangle-shaped base.
• A square pyramid is a pyramid with a quadrilateral foundation.
• Pentagonal pyramids are pyramids with a pentagonal foundation.
• A hexagonal pyramid is one with a base that resembles a standard hexagon.

Prism

Prisms are solids with flat parallelogram sides and identical polygon ends. The following are some traits of a prism: It has a constant cross-section the entire way through.Prisms come in a variety of shapes, including triangles, squares, pentagons, hexagons, and more. Regular prisms and oblique prisms are two other main categories for prisms.

3D images

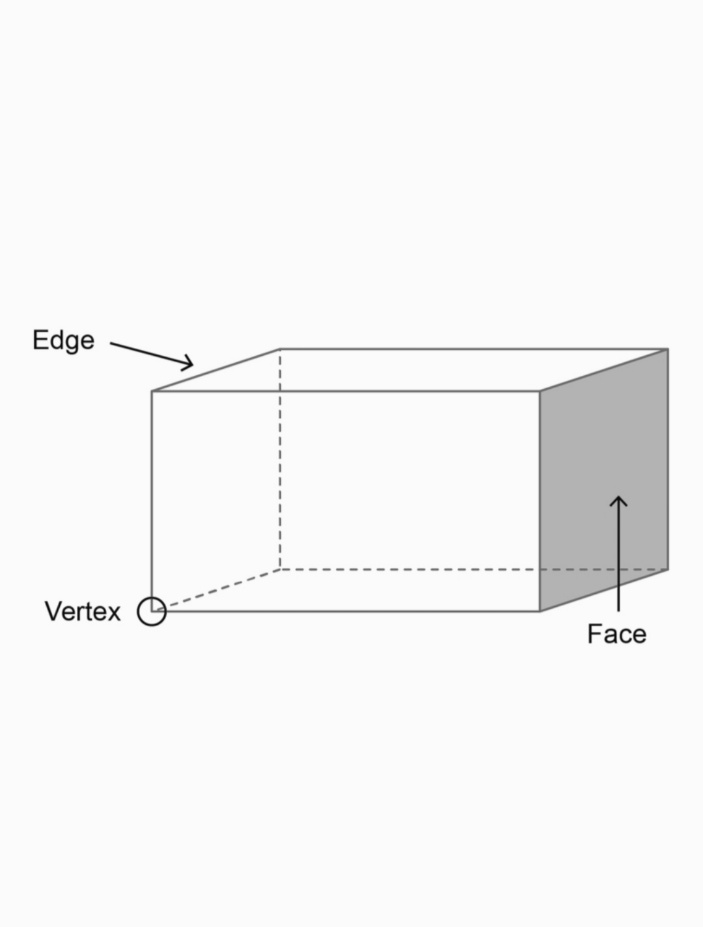
The three dimensions of a three-dimensional object are length, width, and height/depth. They therefore have features like faces, edges, and vertices. All objects that we can touch are three-dimensional, and three-dimensional figures have an inner and an outside.

3D shape nets

A flattened three-dimensional solid is referred to as a net. Similar to how a two-dimensional outline can be folded and combined to create a three-dimensional image. To generate three-dimensional shapes, nets are utilized. More than one net may be present in a three-dimensional shape.

Their nets are what create 3D objects. A net is produced if we take a cardboard box, cut the edges, and flatten it. We may also do the opposite, enlarging the flattened box and glueing it back together to create a 3D cuboid-shaped object. Architects, civil engineers, and graphic designers all employ 3D drawing.

Items with three dimensions

Only distinguishing characteristics that distinguish 3D objects from 2D objects are the width and depth. 3D objects occupy space and have distinct three dimensions, length, breadth, and width. A Rubik’s cube, a book, a box, a carrot, an ice cream cone, and a barrel with a cylinder shape are examples of 3D items that are all around us.

Solved examples

Example 1:

If the side length of a cube is 6 cm, calculate its volume.

Solution:

Side length, a = 7 cm, as stated.

We are aware that a cube’s volume equals three cubic units.

Consequently, \({7^3} = 7 \times 7 \times 7 = 343c{m^3}\)

Consequently, a cube has a volume of \({216 cm^3}\).

Example 2:

Identify the entire surface area of a sphere with a 3 cm radius. Use (π = 3.14)

Solution:

Radius, r = 3 cm, is provided.

The following is the formula to determine a sphere’s total surface area:

TSA of a sphere equals four \({r^2}\) square units.

TSA of the sphere is \(4 \times 3.14 \times {3^2}c{m^2}\)

Sphere TSA = 113.04  \({cm^2}\)

Consequently, a sphere has a total surface area of 113.04\({cm^2}\).

Example 3:

Find the volume of a cuboid with the following measurements: 4 cm, 6 cm, and 12 cm.

Solution:

The dimensions of a cuboid are 4 cm, 6 cm, and 12 cm.

We are aware that a cuboid has a volume of lbh cubic units.

Thus, the cuboid’s volume is equal to (4)(6)(12) \({cm^3}\)

V = 288 \({cm^3}\)

Consequently, the cuboid has a 288 \({cm^3}\) volume.

Frequently asked questions

1.What three-dimensional shapes are there?

In geometry, three-dimensional shapes are those that have length, breadth, and height as their three determined dimensions.

2.What kinds of three-dimensional shapes are there?

Cone, cylinder, cuboid, cube, sphere, rectangular prism, and pyramid are some examples of the various three-dimensional shapes.

3.Does the square have three dimensions?

The shape of a square is two dimensional rather than three dimensional.

4.What is the name of a round object that is three dimensional?

A sphere is a three-dimensional circular form. A football is a spherical item, for instance.

5.What kinds of forms have three dimensions?

Numerous examples of three-dimensional shapes can be found in the real world, including Rubik’s cubes.

If you need extra assistance with topic, You can checkout Solid Shapes( 3D Shapes, Euler’s Formula) in our Class 8 Math course, where we delve into these concepts in depth. By referring to this lesson, you’ll gain a deeper understanding of the material and boost your exam performance. Join our online Math tuition now for personalized attention, expert guidance, and regular assessments to track your progress. Don’t hesitate – start acing your Math class today!

There are two types of shapes: two-dimensional shapes and shapes in flat-plane geometry. They can have any number of sides, and their sides can be either straight or curved. Polygons are plane geometric shapes comprised of lines. Polygons include shapes like triangles and squares. For instance, we can state that 2-D figures are those paper drawings that simply have length and width.

Define Plane

A plane is a two-dimensional surface that can stretch indefinitely in both directions and is measured by two linearly independent locations. In algebra, the points are plotted on a number line that runs continuously and infinitely from left to right, up and down, and in all directions. Two planes can cross each other, be identical to one another, and be in parallel with one another. A plane consists solely of a surface with no depth or width. There are only ever two dimensions. If you imagine a wall and extend it indefinitely, it will turn into a plane.

Plane Figures and Shapes

Squares, rectangles, triangles, circles, pentagons, octagons, hexagons, ovals, and other shapes are examples of plane figures. Circles and ovals are not polygons, but shapes like squares and rectangles that gather together are known as polygons.

A closed two-dimensional or flat surface figure is referred to as a plane shape, as opposed to a solid shape. Instead of having edges and faces, they have a number of thin lines that meet to form a corner or a vertex. Triangles, squares, rectangles, circles, and ovals are some common plane shapes. If we looked closely at a piece of paper, we would see its length and width but not its depth; therefore, since they are created by combining two straight or curved lines, they are closed objects. They are also referred to as polygons or planned geometric shapes.

Examples of Plane Shapes

Squares, rectangles, triangles, circles, pentagons, octagons, hexagons, ovals, etc. are examples of plane shapes.

Triangle: A triangle is a polygon with three sides and three angles.

Quadrilateral: A closed polygon with four sides is referred to as a quadrilateral. Trapezium, Square, Rectangle , rhombus, etc are the examples of quadrilaterals.

Circle: A figure is referred to as a circle if all of its points are equally spaced from a fixed point. The fixed point is referred to as the circle’s center.

Pentagon: A shape is referred to as a pentagon if it has five sides. 

Hexagon: A shape is referred to as a hexagon if it has six sides.

What are Solid Shapes?

What kind of device, a laptop or computer, are you using to read this? Cuboidal! That is correct! Describe a cuboid. It has a strong form. The same applies to cones, cylinders, etc. Solids are shapes that can be observed and measured in three dimensions. Solid shapes are characterized by their length, width, and height, which can also represent thickness or depth. When a two-dimensional object is folded into a three-dimensional shape and put down flat to reveal each face, the result is known as a net pattern. A net is a 3D figure that has been unfolded. Faces, vertices, and edges are the three primary characteristics of solid forms.

Plane Figures and Solid Shapes in your math class? Don’t worry – our online Math tuition can help! We provide comprehensive lessons on these topics, covering everything from basic shapes to more complex geometric figures.

Solid Shapes Examples

Cubes, cuboids, pyramids, prisms, cylinders, spheres, cones, torus, trapezoids, rhombus, parallelograms, and quadrilaterals are a few examples of solid shapes. A pen is made up of two cylinders, and a dome is made up of a hemisphere on a cylinder or a cone. It can also be formed up of two or more actual figures.

Cuboids: Cuboids can be found in everyday objects like bricks, tiffin boxes, books, matchboxes, etc.

Sphere :Globes, marble, oranges, and bubbles are all examples of spheres in everyday life.

Cone: Ice cream cones, traffic cones, party caps, and other objects in everyday life are examples of cones.

Difference between Solid and Plane Figure

Interesting Facts

• When a specific shape is made repeatedly without any gaps or overlapping and covers a plane, the result is a tessellation. Only squares, equilateral triangles, and rectangular hexagons can form regular tessellations.
• Natural tessellation examples include the hexagonal cells in a honeycomb design or the diamond-shaped pattern on a snakeskin.

Solved Examples

1. A cube with a side length of 6 cm has what size surface area?

Ans: The surface area of a cube is \(6{a^2}\).

The area of the surface area is \(6 \times {\left( 6 \right)^2} = 216c{m^2}\)

2. If the radius of a circle is 7 cm, then what is the area of the circle?

Ans: The area of a circle is \(\pi {r^2}\)

The area of a circle is \(\pi {7^2} = \frac{{22}}{7} \times {7^2} = 154c{m^2}\)

Key Features

• Two linearly independent points can be used to measure a plane, which is a two-dimensional surface.
• Squares, rectangles, triangles, circles, pentagons, octagons, hexagons, ovals, and other shapes are examples of plane figures.
• A plane shape is a closed, two-dimensional or flat surface figure.

 

Frequently Asked Questions

1. How has geometry and math gotten so much attention because of the ancient Japanese technique of origami?

Ans: Geometry, mathematics, and engineering have all taken a keen interest in origami, the art of folding paper into three dimensions. It offers a fascinating method for converting a flat plane shape into a solid shape. For instance, methods have been devised for the deployment of airbags in a car and stent implantation from a folded state. A crease pattern can also be folded into a 2D representation. Additionally, it is used to double the cube and trisect an angle.

2. What is Euclidean geometry?

Ans: The study of solid and flat shapes using the axioms and theorems developed by the Greek mathematician Euclid is known as Euclidean geometry (c.300 BCE). The solid and plane geometry is known as euclidean geometry. Angles and circles are two instances of Euclidean geometry. The discipline known as parabolic geometry is based on Euclid’s five postulates. There are two types: solid geometry, which is based on Euclidean geometry in three dimensions, and plane geometry, which is based on Euclidean geometry in two dimensions.

3. What is the point?

In a plane, a point is a dot that has no length, breadth, or height. It establishes a plane’s location. There are two different kinds of points: coplanar and non-coplanar points, as well as collinear and non-collinear points. Non-collinear points do not sit on the same line as collinear points, which are located there. Non-coplanar points do not lie on the same plane as coplanar points, which are parallel to one another.

Introduction

Various geometric parameters such as surface area, volume, etc. to represent the three-dimensional property of a solid. It also indicates the amount of space required to keep an object. The simple geometrical shape we encounter daily includes sphere, cylinder, cube, cone, prism, etc. However, we come to see various objects that are made from a combination of solids. In this tutorial, we will learn about the formula to determine the volume of some known solids and the procedure to evaluate the volume of a combination of solids with solved examples.

What is Combinations of Solids

The combination of solid is the assembly of two or more solids to form a complex one. We cannot rely on simple geometries to meet our daily requirements. Various works require a complex volume that can only be made from a combination of solids. Therefore, combining two or more solids is necessary to get the desired volume. For example, a circus tent can be made by combining two solids, i.e., a cuboid and a cone (as shown in the figure).

There is a basic mathematical concept behind the combination of solids, i.e., the volume of the combined solid is equal to the summation of the volumes of the individual solids. In mathematically,

where V= volume of the solid that is formed after the combination

What is the Volume of Some Commonly Known Solids 

First, we have to know the volume of some simple geometries to find the volume of the combined solid. Here is a list of the volume of some known geometry.

Solved Examples and Word Problems

Example 1:

30 small cylinders are melted and form a larger one. The length and diameter of the small cylinders are 5 cm and 1.4 cm, respectively. Find the length of the large cylinder if the diameter is 2.8 cm.

Solution:

Example 2:

A tent house is made by combining two geometrical structures, i.e., a cylinder and a hemisphere. The height and radius of the cylinder are 20 m and 10 m, respectively. The radius of the hemisphere is 10 m. Find the total volume of the tent house.

Solution:

It is given that, 

The radiusr of the cylinder (r) = 10 m 

The height of the cylinder (h) = 20 cm

Now, the volume of the cylinder can be obtained by using the formula

Example 3:

A hemispherical part has been removed from a cube in such a way that the diameter of the hemisphere is equal to the side length of the cube. The radius of the hemisphere is 2 cm. Find the remaining volume after removing the hemispherical part. 

Solution:

The remaining volume after removing the hemispherical part can be determined by subtracting the volume of the hemisphere from the volume of the cube. 

Hence, the volume of the remaining portion is = V=\({V_c-V_h}\)

⇒V=64-16.75=47.25 \({cm^3}\)

∴ The volume of the remaining portion is found to be 47.25\({cm^3}\)

Summary

The present tutorial gives a brief introduction about the volume of a combination of solids. It is based on a basic mathematical concept, i.e., the volume of the combined solid is equal to the summation of the volumes of the individual solids. In addition, the formulae to determine the volume of some known geometries have been depicted in this tutorial. Moreover, some solved examples have been provided for better clarity of this concept. In conclusion, the present tutorial may be useful for understanding the basic concept of the volume of a combination of solids.

Expand your knowledge of mensuration with our 88guru’s online maths tuitions! Join now to learn about other interesting topics. With our 4-day free trial, you can experience the quality of our teaching before committing. Don’t miss out on this opportunity to enhance your mathematical skills!

Frequently Asked Questions

1. Can we determine the volume of an irregular solid?

The volume of an irregular solid cannot be evaluated using the basic formulae that are given in this tutorial. We have to use some other techniques.

2. Will the surface area of the solid geometry equal to the addition of the individual surface area of the solids?

In combination of solids, only volume remains conserved. The surface area of the combined object may or may not equal the addition of individual surface areas of the solids. 

3. Give some real-life examples of combinations of solids.

The real-life examples of the combination of solids include ice cream (combination of cone and hemisphere), house (combination of cuboid and hemisphere), etc.

4. If a large spherical ball is cut into two halves, then the sum of the surface area of the two halves will be equal to or larger than the original sphere?

The addition of the surface area of two smaller spheres will be larger than the original sphere. However, the addition of volume will remain unchanged.

5. What is the meaning of volume?

The volume is a geometrical parameter that refers to the capacity of holding by an object. It is also defined as the space occupied by a solid object.

Introduction

In our daily activities, we encounter many objects of various shapes and sizes. All shapes are defined by a specific number of faces, vertices, and edges.

Cube, parallelepiped(cuboid), cone, cylinder, sphere, triangular pyramid, rectangle, and prism are examples of three-dimensional solids. A body or 3D object has three dimensions: length, width, and height. Solids have faces, edges, and vertices. As a result of these three dimensions (l, w, h), these solid shapes and objects have faces, edges, and corners.

Polyhedrons: Definition

Polyhedrons are 3D shapes with straight edges, flat faces, straight edges, and sharp vertices (corners). The word “polyhedron” comes from the Greek word, “poly” which means “many” and “polyhedron” means “area or surface”. Therefore, when many planes are joined together, they form a polyhedron. These shapes are named according to their faces, which are usually polygons. The most common names are cubes, hexahedrons, etc.
A polyhedron is a three-dimensional solid made up of polygons. It has a flat surface, straight edges, and corners. For example, a cube, prism, or pyramid is a polyhedron. Cones, spheres, and cylinders are not polyhedra because their sides are curved rather than polygonal. 

Vertices

The vertices of a geometry can be defined as corners. In the other words when referring to a polygon (any straight-sided, closed 2-D figure, such as a triangle or rectangle), a vertex simply means a corner point where 2 adjacent straight lines meet. The word vertex refers to the point, not the angle.
When dealing with higher dimensions, a similar concept applies. In 3D a point wherever 2 or additional edges meet is called a vertex.

For example: Consider a rectangle: It has four vertices (plural of vertex). Because it has four corners and at every corner 2 edges meet.

Similarly, 

• There are 8 vertices in the cube and cuboid. 
• One vertex in the cone
• Spheres and Cylinders haven’t any vertex because their surface is curved. 

Edges

The line segment between the faces is called an edge. For solid shapes, a line section wherever 2 faces meet is understood as an edge. For a polygonal shape, we will say that an edge may be a line section on the boundary connecting one vertex (corner point) to a different.

For example, a pentagon has five edges.

The line segments that type the skeleton of the 3D shapes square measure are referred to as edges.

Faces

A flat surface is called a face. In the others words A  face is a single surface of a solid body. For example, a tetrahedron has four faces. 

Number of Vertices, Edges, and Faces in commonly known polyhedrons

Counting Faces: To count the number of faces, we have to find the number of flat sides.

Now, number of faces in the following shapes are:

Cube = 6

Cuboid = 6

Cylinder = 3

Cone = 2

Sphere = 1

Counting Edges: To count the number of edges, we have to find the number of the line segment between the faces.

Number of edges in the following shapes are:

Cube = 12

Cuboid = 12

Cylinder = 2

Cone = 1

Sphere = 0

Counting Vertices: To count the number of vertices, we have to find the number of corners.

Number of vertices in the following shapes are:

Cube = 8

Cuboid = 8

Cylinder = 0

Cone = 1

Sphere = 0

Euler’s Formula

Now from the above topics we get the concept of faces ,edges and vertices and now we will know about Euler’s formula for polyhedra that usually deals with shapes known as solid shapes. This formula specifies the relationships between faces, edges, and vertices.

Euler’s formula can be expressed as:

F + V- E = 2

Where, F denotes the number of faces, V denotes the number of vertices, and E denotes the number of edges.

For more help, you can Refer to our video in Class 8 Maths in Lesson no 27 Euler’s Formula. Check out the video Lesson for a better understanding.

Solved Examples

Example1: Can a polyhedron have 11 faces, 22 vertices, and 33 edges? 

Solution: This can be verified easily by Euler’s formula.  

F + V – E = 2

Given, faces(F) = 11

Vertices (V) = 22

Edges(E) = 33

Now putting these in the above formula, 

LHS =F + V – E

        =11+22-33= 0

RHS = 2

LHS does not equal RHS. 

Hence , There is no polyhedron for the given conditions. 

Example 2: Find the  number of faces, edges, and vertices for a triangular prism?

Solution: A prism may be a solid that has five faces, six vertices, and nine edges.

Example 3: How many vertices (corners) does a cube have?

Solution: 8.

Example 4: How many faces, edges, and corners does a pentagonal prism have?

Solution: The pentagonal prism has 7 faces, 15 edges and 10 corners.

Example 5: How many faces, edges, and corners does a Triangular Pyramid have?

Solution: A Triangular Pyramid has 6 edges, 4 corners, and 4 faces.

Example 6: Which of the following solids has a curved edge?

Solution: Cone: A cone has just one edge which is curved – it is a circle.

Cube: A cube has 12 straight edges.

Triangular prism: A triangular prism has 9 straight edges.

Triangular pyramid: A triangular pyramid has 6 straight edges.

Example 7: A solid has 14 faces and 12 vertices. How many edges does the solid have?

Solution: Polyhedral Formula/Euler’s Formula = F + V – E = 2

Therefore, 14 + 12 – E = 2.

or,26 – E = 2

or, E = 26 – 2 = 24

or,E = 24

Therefore, the solid has 24 edges.

Example8: How is a cone defined in terms of faces, edges, and vertices?

Solution: 2 faces, 1 edge, and 1 vertex. 

One of the faces is the circular base, the other is the continuous curved part.

The one and only edge is the edge of the circular base, where the two faces meet.

The vertex is the point at the top (the sharp corner).

Summary

• The vertices of a geometry can be defined as corners.
• The line segment between the faces is called an edge.
• A flat surface is called a face.
• Vertices, faces, and edges are three properties that define any 3D or 2D body.
• A polyhedron is a three-dimensional solid made up of polygons. It has a flat surface, straight edges and corners.
• Euler’s formula = F + V – E = 2. 

 

Frequently Asked Questions

1. What do you mean by vertices also give one example?

The vertices of a geometry can be defined as corners. For example: Consider a rectangle: It has four vertices (plural of vertex). Because it has four corners and at every corner 2 edges meet.

2. What is faces? Give one example.

A flat surface is called a face. In the others words A  face is a single surface of a solid body. For example, a polyhedron has four faces. 

3. What do you mean by edges? Give one example.

The line segment between the faces is called an edge. For example, a pentagon has five edges.

4. What is the relation between vertices, edges, and faces?

Euler’s  formula specifies the relationships between faces, edges, and vertices.

Euler’s formula can be expressed as:

F + V- E = 2

5. What is solid shape?

A solid is a 3D shape with length, width, and height (depth). Cube, cone, sphere, and rectangular parallelepiped are examples of three-dimensional shapes.

Introduction

When a number (n) is multiplied three times, the result is known as the cube of that number. As a result, the cube of the number (n) is \({n^3}\) or n-cubed. Select the number 4 as an example. We already know that . As a result, 64 is known as the cube of 4. The cube root of a number, on the other hand, is the inverse of the cube of a number and is denoted by \(\sqrt[3]{{}}\) In the same example, 4 is called the cube root of 64. Let’s go ahead and learn more about the numbers’ cubes and cube roots.

What is a cube of a number?

A cube number is an outcome of multiplying an integer by the same integer three times. They also go by the name “perfect cubes,” or cube numbers. For example, \(4 \times 4 \times 4 = {4^3} = 64\). A  number multiplied by the same number three times is called a cube number, or a number with the exponential power of three. Because a negative number produces a negative number when it is multiplied by the same negative number three times, cube numbers of positive numbers are positive, while cube numbers of negative numbers are negative. For example, \({\left( { – 6} \right)^3}\)

In geometry, a cube’s volume is equal to the product of its length, breadth, and height. The length, breadth, and height are all equal inside the cube because it is a cube. The cube’s volume is therefore equal to , which  is its length, height, and width. This implies that a cube’s volume is a cube number.

What are the cube roots?

When we hear the word cube root, the first two words that come to mind are cube and roots. In this sense, the concepts are somewhat similar; “root” refers to the primary source of origin. As a result, we only need to consider “which number’s cube must be chosen to get the given number.”

In a nutshell, the cube root of any number is the factor that is multiplied three times to obtain the specific values. Keep in mind that a number’s cube root is the inverse of the number’s cube.

Cube roots by prime factorization

The prime factorization method can be used to calculate the cube root of a number. Begin by determining the prime factorization of a given number to find its cube root. Then, divide the obtained factors into groups, each having three identical factors. Then, to get the answer, eliminate the symbol of the cube root and multiply the factors. If any factor remains that cannot be equally divided into sets of three, the given number isn’t a perfect cube, and we cannot determine its cube root. 

Example: How to determine the cube root of 10648.

 

\(\begin{array}{l}\sqrt[3]{{10648}} = \sqrt[3]{{2 \times 2 \times 2 \times 11 \times  \times 11 \times  \times 11}}\\\;\;\;\;\;\;\;\;\;\;\; = 2 \times 11 = 22\end{array}\) 

Cube roots by estimation

If a number has several digits, it will be difficult for you to use the prime factorization and long division methods to compute the square and cube roots of the number. You will thus attempt to estimate the cube root and square root values for these numbers. Factorization becomes challenging as the number of digits rises. Estimating a square root and a cube root in such circumstances is a wise move.

The following step can be used to determine a large integer’s cube root using the estimation method if it is claimed that the provided number is a perfect cube.

Step 1: Starting with the rightmost digit, create a group of three digits starting with any cube number, such as 19683, whose cube root needs to be found.

Step 2: The unit’s digit of the necessary cube root will be provided by the first group. Since the unit digit is 3, we need to find the cube root of the cube which also has unit digit 3, i.e., \({7^3} = 343\) has unit digit 3. Hence, our unit digit for the cube root is 7.

Step 3: Now take the second group, i.e., 19, and find the cube root that is just smaller than 19 ( second group ).

\({2^3} < 19 < {3^3}\).

8 or  is just smaller than 19 hence our tenths place digit is 2.

Hence, the cube root of 19683 is equal to

\(\sqrt {19683}  = 27\)

Solved examples

Example 1: Determine the following:

1. \(\sqrt[3]{{729}}\)

Solution: We will be using the prime factorization method.

From it, we will get

Now operate both the sides under the cube root.

\(\begin{array}{l}\sqrt[3]{{729}} = \sqrt[3]{{3 \times 3 \times 3 \times 3 \times 3 \times 3}}\\\;\sqrt[3]{{729}} = 3 \times 3 = 9\end{array}\)

2. \(\sqrt[3]{{1728}}\)

Solution: We will be using the prime factorization method.

From it, we will get

Now operate both the sides under the cube root.

\(\begin{array}{l}\sqrt[3]{{1728}} = \sqrt[3]{{2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 3 \times 3 \times 3}}\\\;\sqrt[3]{{1728}} = 2 \times 2 \times 3 = 12\end{array}\)

3. \(\sqrt[3]{{2744}}\)

Solution: We will be using the prime factorization method.

From it, we will get

Now operate both the sides under the cube root.

\(\begin{array}{l}\sqrt[3]{{2744}} = \sqrt[3]{{2 \times 2 \times 2 \times 7 \times 7 \times 7}}\\\;\sqrt[3]{{2744}}\; = 2 \times 7 = 14\end{array}\)

Example 2: Determine the cube root of 59319 using estimation.

Solution:

The given number is 59319

First, we have to make the group of three from the right side. So we have the first group (319) and the second group (59).

To find the unit digit of the cube root, we have to find the cube that has the unit digit equal to the unit digit of the first group.

\({9^3} = 729\)

The cube of 9 has the unit digit 9, so our unit digit of the cube root is 9.

Now take the second group 59 and find the cube root that is just smaller than 59.

\({3^3} < 59 < {4^3}\).

27 or \({3^3}\) is just smaller than 59, hence our tenth place digit is 3.

Hence, the cube root of 59319 is equal to

\(\sqrt {59319}  = 39\)

Summary

When we hear the word cube root, the first two words that come to mind are cube and roots. In this sense, the concepts are somewhat similar; “root” refers to the primary source of origin. As a result, we only need to consider “which number’s cube must be chosen to get the given number.” The cube root of any number is the factor that is multiplied three times to obtain the specific values. Keep in mind that a number’s cube root is the inverse of the number’s cube.

When we say n is a cube root of m, then we can denote it as \(\sqrt[3]{m} = n\), with a small 3 written on the top left of the sign. The radical sign \(\sqrt[3]{{}}\)  is used as a cube root symbol for any number. Another way to express cube root is to write 1/3 as a number’s exponent. In cube roots, negative values are allowed, unlike in square roots,

For example, \(\sqrt[3]{{ – 216}} =  – 6\)

If you’re struggling with the concept of finding the cube root of a number, don’t worry – we’re here to help! Check out our video lesson no. 15 in 88guru’s online Math tuition for 8th class students.

Frequently Asked Questions

1. State the definition of cube root.

Ans: The cube root of any number is the factor that is multiplied three times to obtain the specific values. Keep in mind that a number’s cube root is the inverse of the number’s cube.

2. How is a cube root different from a square root?

Ans: A cube root is a number that when cubed yields the wanted number, whereas a square root yields the wanted number when squared. Furthermore, in cube roots, negative values are allowed, unlike in square roots.

3. What is the name of the method used for finding cube roots?

Ans: The prime factorization method is used to calculate the cube root of a number.

4. What is the cube root of 125?

Ans: 125 is a perfect cube, and 5 is the cube root of 125.

5. How Can a Cube Root Be Simplified?

Ans: The prime factorization method can be used to simplify the cube root. First, prime factorize the given number and then extract the common factors in groups of three. To find the answer, multiply these common factors by two.

Introduction

The three dimensions of a cuboid are known as the length, breadth, and height, and the volume of the cuboid depends on these parameters. As is the norm, the volume is measured either in cubic units of length like \({cm^3}\), \({m^3}\),  etc., or we can measure the volume in units of litres and millilitres. The choice is a matter of convenience.

What is a Cuboid

A cuboid is a solid rectangular box with six faces, all of which are rectangles. The rectangles that lie opposite to each other are parallel while those that are adjacent intersect each other at right angles. You can think of a cuboid as a solid rectangle in three dimensions. The figure given below illustrates it better.

A cuboid

The cuboid shown above has six rectangular faces denoted as a, b, c, d, e, and f. The front and back faces, a and b respectively, are congruent rectangles that are parallel to each other. Likewise, the top and bottom faces, c and d respectively, lie parallel to each other and are congruent, just as the side faces e and f are parallel to each other.

What is the volume of a Cuboid?

As previously mentioned, the volume of a cuboid measures the space it occupies in three-dimensional space and is dependent on its dimensions. For a cuboid, the volume is simply the product of its length, breadth, and height. That is,

𝑉=𝑙𝑒𝑛𝑔𝑡h ×𝑏𝑟𝑒𝑎𝑑𝑡h× h𝑒𝑖𝑔h𝑡  

This volume can be measured in any unit of volume like \({cm^3}\), litres, millilitres, etc. The figure given below shows the 3 dimensions.

Cuboid dimensions

Notice how this formula also means that the volume equals the area of the base times the height of the cuboid. Thus, calculation of the area of a cuboid is a fairly easy task. However, it must be noted that the units must be consistent while performing any calculations. If the dimensions aren’t provided in the same units, we can end up with skewed and wrong results.

Also Read: How to Calculate the Volume of a Sphere

Solved Examples

1. A cuboid has dimensions 10 cm x 5 cm x 4 cm. Find its volume.

Solution

Given length = 10cm, breadth = 5cm, and height = 4cm.

We have the formula for the volume, which says that 𝑉=𝑙𝑏h 

. And since all measurements are provided in cm3 only, no unit conversions are required. Therefore,

𝑉=𝑙𝑏h 

𝑉=10×5×4 

𝑉=200  \({cm^3}\)

Therefore, the volume of the cuboid is 200 \({cm^3}\).

2. Given a cuboid with length, breadth, and height of 7m, 300cm, and 2m respectively, find its volume in cubic metres.

Solution

Given length = 7m, breadth = 300cm, and height = 2m, we need to calculate the volume. However, this time, one of the dimensions is provided in centimetres instead of metres and we will need to convert it before applying the formula. We know that

1 𝑚=100 𝑐𝑚 

∴300 𝑐𝑚=3 𝑚 

Now we can apply the formula we have.

𝑉=𝑙𝑏h 

𝑉=7×3×2 

𝑉=42  \({m^3}\)

Word Problems

1. How much water can be poured into a cuboidal tank that is 6m long, 5m wide, and 3m high?

Solution 

Given length = 6m, breadth = 5m, and height = 3m. All units are consistent, and we can directly apply the formula. Thus,

𝑉=𝑙𝑒𝑛𝑔𝑡h× 𝑏𝑟𝑒𝑎𝑑𝑡h × h𝑒𝑖𝑔h𝑡 

𝑉=6×5×3 

𝑉=90 \({m^3}\)

Therefore, the volume of the tank is 90 \({m^3}\).

Summary

This tutorial discussed the cuboid shape and its volume. We learned that the volume of a cuboid is simply the product of its dimensions, which include the length, breadth, and height.

Frequently Asked Questions

1. What is the shape of the face of a cuboid and how many faces does a cuboid have?

A cuboid is a solid rectangle, and it has six faces. Pairs of opposite faces are congruent to each other.

2. What is the difference between a cube and a cuboid?

A cube is a special type of cuboid whose length, breadth, and height are all equal, i.e., it has square faces. On the other hand, a cuboid has rectangular faces with differing length, breadth, and height.

3. What is the difference between the volume of a cube and the volume of a cuboid?

There isn’t much difference in the way volumes are calculated for the cube and the cuboid. In fact, the formula for the volume of a cube is 𝑉= \({a^3}\)

, which is basically the same as that for the cuboid since here, the length, breadth, and the height are all equal to a.

4. How many sides, faces, and vertices are there in a cuboid?

A cuboid has 12 sides, 6 faces, and 8 vertices.

Introduction

A sphere is a three-dimensional object which has a circular cross-section everywhere, and its volume is the space it occupies. This volume is determined by the radius of the sphere and is measured in cubic units. You can find a large number of practical examples of spherical objects, which include cricket balls, basketballs, volleyballs, and so on.

What is a Sphere

A sphere is a three-dimensional solid figure that has a round shape and every single point on the surface is equidistant from its centre. The distance between the centre and any point on the surface is known as the radius and commonly denoted by “r”. Owing to its unique shape, the sphere is one of the very few shapes in geometry that have no edges or vertices. Depending upon the way the sphere is created, we can classify it into solid sphere or a hollow sphere.

Sphere

The image above shows a sphere with a few cross-sectional areas, and we can notice that when sliced in any direction, we get a circle. In fact, if viewed in two dimensions, a sphere would look just like a circle. The main difference is that a sphere is a three-dimensional figure and thus, has a specific volume. On the other hand, a circle is two-dimensional and has no volume. The figure below shows a sphere with its centre and radius marked, along with a point on its surface.

Sphere

What is the volume of a Sphere?

Solid Sphere

The sphere occupies a finite amount of space in the three-dimensional space. This is measured by its volume, and it depends upon how large the sphere is, or in other words, the radius of the sphere.
The formula for calculating the volume of a sphere is given by:

\(V = \frac{4}{3}\pi {r^3}\)

Here, r represents the radius of the sphere, which is half of its diameter. π is a universal constant whose value is approximately equal to 3.14. In terms of the diameter, we can write the volume as

\(V = \frac{1}{6}\pi {d^3}\)

The above formula also shows us that the volume of the sphere depends on the third power of the radius. This means that even a slight increase in radius will drastically increase the volume of the sphere. Mathematically, we can write that

\(V\alpha {r^3}\)

Volume of Hollow Sphere

The formula we just saw was valid for a solid sphere. However, we can also have a hollow sphere, which is a solid sphere from which, a smaller sphere has been taken out and we are left with a shell. In that case, we can simply subtract the volume of the sphere that was taken out. Let R be the outer radius of the sphere and r be the inner radius. We can then write

\((V = \frac{4}{3}\pi ({R^3} – {r^3})\)

Solved Examples

1. Calculate the volume of a sphere of radius 5 cm.

Solution

We are given that the radius is r = 5cm. The volume of a sphere is given by the formula

\(V = \frac{4}{3}\pi {r^3}\)

Hence, we have,

\(\begin{array}{l}V = \frac{4}{3} \times 3.14 \times {5^3}\\V = 523.59c{m^3}\end{array}\)

2. A hollow sphere is constructed such that its inner and outer radii are 3cm and 5cm, respectively. Find its volume.

Solution

Given that the radius of the inner sphere r = 3cm. The volume of a hollow sphere is given by the following formula:

\(V = \frac{4}{3}\pi ({R^3} – {r^3})\)

Here, R = 5 cm. Therefore, we have

\(\begin{array}{l}V = \frac{4}{3} \times 3.14 \times ({5^3} – {3^3})\\V = \frac{4}{3} \times 3.14 \times (125 – 27)\\V = \frac{4}{3} \times 307.72\\V = 410.3c{m^3}\end{array}\)

Hence, the volume of the hollow sphere \( = 410.3c{m^3}\).

Hence, the volume of the hollow sphere \( = 410.3c{m^3}\).

Word Problems

1. How much air can a spherical balloon of radius 7m hold without bursting?

Solution

Given that the radius of the sphere, r = 7m. The balloon can only hold as much air as its volume before it bursts. Thus, our job is to find its volume. We know that

\(\begin{array}{l}V = \frac{4}{3}\pi {r^3}\\V = \frac{4}{3} \times 3.14 \times {7^3}\\V = 1436.7{m^3}\end{array}\)

Thus, the balloon can hold a maximum of \(1436.7{m^3}\) of air without bursting.

Summary

This tutorial discussed the basics of sphere, and we developed an understanding of its volume by solving a few examples and word problems.

Frequently Asked Questions 

1. Why isn’t it possible to calculate the volume of a circle?

A circle is a two-dimensional shape that has no defined volume. The space it occupies is given by its surface area and we have no defined volume for a circle.

2. The volume of a sphere depends on which dimensions of the sphere?

The volume of the sphere \( = \frac{4}{3}\pi {r^3}\), so the volume of a sphere depends on only the radius of the sphere. The volume of the sphere ∝ the radius of the sphere

3. Given two spheres of different radii, what would be the ratio of their volumes?

Since the volume of a sphere depends in its radius raised to the third power, the ratio of the spheres’ volumes would be equal to the ratio of the cubes of their radii. That is,

\(\frac{{{V_1}}}{{{V_2}}} = {\left( {\frac{{{r_1}}}{{{r_2}}}} \right)^3}\)

Introduction

It is important to understand prime numbers before we start figuring out how to find them. Numbers with only two factors, i.e., 1 and the number itself, are known as prime numbers. When we are given a number that is small, it is easy to figure out whether it is a prime number or not. However beyond two digits, the task becomes difficult and we have different tricks and theorems one can use.

In this article, we will discuss prime numbers as well as their identification, the consecutive prime formula, and also solve a few problems so you can better understand this concept.

What are prime numbers?

For a number to be prime, it should be a whole number divisible only by 1 or by itself. For instance, if we try to find the factors of 89, we will see that it is not divisible by any number other than 1 or itself and thus, is a prime number.

Here are a few properties of prime numbers:

• Any positive integer larger than 2 can be written as the sum of two prime numbers.
• Two prime numbers are always coprime.
• The only even prime number is 2 and all the remaining prime numbers are odd.
• The prime factors of each composite number are distinct.

How to identify if a number is prime

Since a prime number is only divisible by one or itself, an easy check for smaller numbers is to factorise them and check whether they have other factors. This involves the following steps.

Step 1: Find out the factors of the number in question.

Step 2: Determine how many does factors it has.

Step 3: If there is a total of more than two factors, the number isn’t prime.

For instance, 85 has a number of factors and as soon as you encounter the fact that it is divisible by 5, it is no longer prime. However, this method is not suitable for larger numbers since it becomes very time-consuming.

Let’s check 95 now. This time, we will utilise a clever trick that works as follows:

Step 1: Find the square root of the number given. In this case, it is \(\sqrt {95}  = 9.74 \approx 9\)  (we take the integer value).

Step 2: Select all prime numbers below the answer we have just derived (9) and see if they divided the number we are given.

Step 3: Upon doing so, we discover that 95 is divisible by 5 and thus, it is not a prime number.

Consecutive prime formula

While there is no general formula for giving us consecutive prime numbers, we can utilise a few tricks:

• Except for the 2 and 3, all prime numbers can be represented in the form \(6n \pm 1\), where n is a natural number.
• For prime numbers greater than 40, the following formula holds: Let n = 0, 1, 2,….., 39, then \({n^2} + n + 41\) gives us prime numbers.

Solved Examples

Example 1: Is 23 a prime number?

Solution:  To check whether 23 is prime or not, we have two approaches:

Approach 1:

We can check whether it fits on the pattern of \(6n \pm 1\). If we put n = 4, we get \(6n – 1 = 23\) and thus, we can say it may be prime.

Approach 2:

We can factorise 23 and we see that it only has the factors 1 and 23. Thus, both approaches confirm that it is a prime number.

Example 2: Is 61 a prime number?

Solution: For prime numbers greater than 40, we use the formula we just discussed. Let \({n^2} + n + 41\), where n=0,1,2….,39

Upon solving, we find that if n = 4, we get the answer as 61 and thus, 61 is a prime number.

Example 3: Check whether 24 is a prime number.

Solution: We start by finding its prime factors

\(\begin{array}{l}\begin{array}{*{20}{l}}{24{\rm{ }} = {\rm{ }}1{\rm{ }} \times {\rm{ }}24}\\{24{\rm{ }} = {\rm{ }}2{\rm{ }} \times {\rm{ }}12}\\{24{\rm{ }} = {\rm{ }}3{\rm{ }} \times {\rm{ }}8}\end{array}\\24{\rm{ }} = {\rm{ }}4{\rm{ }} \times {\rm{ }}6\end{array}\)

Thus, 24 has numerous factors, including 1, 2, 3, 4, 6, 8, and 12. Thus, it is not a prime number.

Summary

• A whole number divisible only either by one or by itself is called a prime number.
• A prime number larger than one has only one prime factor, i.e., itself.
• Any positive integer greater than 2 can be written as a sum of two prime numbers.
• Two prime numbers are always coprime.
• 2 is the only even prime number.
• The most basic way to check whether a number is prime is to factorize it. If it has more than two factors, it is not a prime number.
• All prime numbers greater than 3 can be written in the form \(\;6n \pm 1\), where n is a natural number.
• Prime numbers greater than 40 can be written in the form \({n^2} + n + 41\), where n goes from 0 to 39.

Frequently Asked Questions

1. What are prime numbers?

Numbers that can only be divided by one or by themselves are called prime numbers.

2. What is the formula to calculate prime numbers above 40?

Prime numbers greater than 40 can be written in the from \({n^2} + n + 41\), where n goes from 0 to 39.

 3. Is it possible that a number is both composite and prime?

No. The conditions of being prime and being composite are contradictory. However, the number 1 is said to be neither prime nor composite.

4. What are composite numbers?

Composite numbers are the opposites of primes. These are numbers which have more than two factors.

5. State some properties of prime nunumbers.

• Two prime numbers are always coprime.
• Any positive integer greater than 2 can be written as the sum of two prime numbers.
• A prime number is a positive integer greater than 1.
• It is only divisible by 1 and itself.
• Every prime number has exactly two distinct factors, namely 1 and the prime number itself.
• There are infinitely many prime numbers.
• The first five prime numbers are 2, 3, 5, 7, and 11.
• Every integer greater than 1 can be expressed as a product of primes, and this factorization is unique up to the order of the factors. This is known as the Fundamental Theorem of Arithmetic.
• Prime numbers are important in number theory and have applications in cryptography and other areas of computer science.

Introduction to the concept of Symmetry

The word “symmetry” is frequently utilized in daily life; instances include the symmetry of butterfly wings, architectural designs, and more. Do you recognize symmetry? When a figure can be folded into two identical halves, we say that it is symmetrical, and as a result, this phenomenon is referred to as symmetry. The line that divides a figure into two identical sections is known as the line of symmetry. In this essay, the two primary symmetries—rotational symmetry and line symmetry—will be adequately explained.

Definition of Line Symmetry and Rotational Symmetry

Line Symmetry

 Line symmetry is a type of symmetry that involves reflections. When an object has at least one line that splits a figure in half, with one half being the mirror image of the other, this is referred to as line symmetry, also known as reflection symmetry. The symmetry line might be vertical, diagonal, horizontal, slanted, etc. An imaginary axis or line that splits a figure into two identical halves is called a line of symmetry.

Rotational Symmetry 

A fixed point is the centre of many objects. A windmill, a car’s wheels, a clock’s hands, a fan’s blades, etc. are a few examples. When anything rotates, its size and shape stay the same. Rotational symmetry is the ability of a shape to retain its appearance after a revolution. Rotations can occur both in a clockwise and anticlockwise direction. A form or item that keeps its appearance after a given amount of rotation by partial turn has been applied has rotational symmetry.

Therefore, a figure is considered to have rotational symmetry if it fits onto itself more than once throughout a full rotation. A square is being spun here. No matter how it is rotated, the square appears unchanged. As a result, the square acquires rotational symmetry.

Line of Symmetry

An imaginary axis or line that can be used to divide a figure into its symmetrical halves is referred to as a “line of symmetry” in mathematics. It is often referred to as the axis of symmetry. The line symmetry is also called a mirror line because it exhibits two coinciding reflections of the same image. Consequently, it also has a form of reflection symmetry. In most cases, it splits an object in half.

Order of Rotational Symmetry

The number of distinct orientations in which a form maintains its inherent shape is related to the order of rotational symmetry of that shape. A complete turn or full turn is a rotation of \(360\)  degrees. In a full turn, there are primarily 4 rotational positions.

rotation of \(90\) degrees.

rotation of \(180\)  degrees.

rotation of \(270\) degrees.

rotation of \(360\) degrees.

Shapes of Line Symmetry and Rotational Symmetry

Now we know that some shapes have line symmetry and some have rotational symmetry. Some shapes, respectively, have rotational and line symmetry. We’ll discuss some items’ symmetry right now, which demonstrates both kind of symmetry.

Square: A square \(ABCD\) will always fit exactly onto itself when rotated through \(90\),\(180\),\(270\), and \(360\) degrees about the point \(O\). It has rotational order symmetries as a result. The diagonals and the lines connecting the middles of the opposing sides make up the square’s additional four symmetry lines.

Rectangle: A rectangle \(ABCD\) will always fit exactly onto itself if it is rotated between \(180\)and \(360\) degrees. It has \(2\) rotational order symmetries as a result. Additionally, it has two lines of symmetry.

Equilateral Triangle: An equilateral triangle ABC always fits exactly onto itself when rotated through \(120\),\(240\), and \(360\) degrees about the centroid \(O\). Therefore, the rotational symmetry is of order \(O\). The triangle additionally has three lines of symmetry along the bisectors of the internal angles.

Interesting facts

• Every single regular polygon is symmetrical in shape. If a figure’s rotational symmetry is \(180\) degrees, it has point symmetry.
• The number of sides equals the number of symmetry lines.

Solved Example

Find out the shapes from below, which do not have rotational symmetry

Solution:

1. As everyone is aware, rotational symmetry is a type of symmetry where, after rotating a shape in a certain direction, the new shape is the same as the original.
2. The preceding figure demonstrates that (b) and (a) lack rotational symmetry as a result.
3. There are more symmetric forms, such as the point, translational, gliding, reflectional, helical, etc., but they fall outside the scope of what is now known.

Conclusion

This article provided comprehensive information on line symmetry and rotational symmetry. The rotational symmetry order was also revealed to us. In addition, we discovered the shapes with rotational and line symmetry.

Frequently Asked Questions 

1. What do line symmetry and rotational symmetry mean?

If a figure is the same on both sides of a line, it is said to be symmetrical. When a figure can be rotated while keeping its original appearance, it exhibits rotational symmetry.

2. What sets lines of symmetry apart from other lines of symmetry?

The line that divides a figure into two identical sections is known as the line of symmetry. If the shape of an object stays the same when a line is drawn through the middle of it, it possesses line symmetry.

3. In mathematics, what is rotational symmetry?

A form is said to have rotational symmetry if it keeps its appearance after a revolution. Rotations can happen both clockwise and anticlockwise. An object or form’s size and shape don’t change while it rotates. Instead, it revolves around a predetermined location known as the rotating center. This phenomenon is referred to as rotational symmetry.

4. Do right triangles have symmetry along their lines?

A right-angled triangle has non-symmetrical lines. A symmetry line is absent. There is only rotational symmetry of order. The right triangle is isosceles if it only contains one line of symmetry.

Introduction

The relationship between a number and its square root is important to understand. Squaring a number means multiplying it by itself, while finding the square root of a positive number involves finding the number that, when squared, results in the original number. For example, if the square of a number p is q, then the square root of q is equal to p. 

As an example, 2 squared is 4, and the square root of 4 is either +2 or -2.

What is a square of a number?

The square of a number is defined as the product of the number with the number itself. This is represented by a superscript 2 in front of the number. Here are a few examples.

• squared is \(2 \times 2 = {2^2} = 4\)
• 3 square is \(3 \times 3 = {3^2} = 9\)
• 4 square is \(4 \times 4 = {4^2} = 16\)

Square roots

What are square roots?

The square root operation is the inverse of squaring a number. Basically, it is the number which, when multiplied by itself, gives the number whose square root we are trying to find. The square root is operated by the radical symbol \(\sqrt {} \) and the number inside the radical is called the radicand.

Hence, given a number , its square root is represented by \(\sqrt p \)  and if we square \(\sqrt p \) we arrive back at the original number. Thus,

\(\sqrt p  \times \sqrt p  = \sqrt {{p^2}}  = p\)

Square root symbol

The square root function, which is a one-one function, takes a positive number and yields its square root. If it is provided a negative number, the answer is complex.

\(f\left( a \right) = \sqrt a \)

Example: The square root of 4 is equal to \(\sqrt 4  =  \pm 2\)

The square root of 9 is equal to = \(\sqrt 9  =  \pm 3\)

The square root of 16 is equal to = \(\sqrt {16}  =  \pm 4\).

Square roots by prime factorization

We can find the square root of a number by using the prime factorisation method.

1. We start by finding out the prime factors of the number.
2. We then group the same factors into pairs of two.
3. We then take one number each from these pairs and multiply them together. The product we thus obtain is the square root we need.

Example: Find the square root of 36 by using the prime factorization method.

Upon factorising 36, we see that the prime factors come out to be

\(36 = 2 \times 2 \times 3 \times 3\)

We now group the same numbers together

\(36 = \left( {2 \times 2} \right) \times \left( {3 \times 3} \right)\)

And then take one number from each pair. The product thus obtained is the square root. Hence

\(36 = {\left( {2 \times 3} \right)^2} = {6^2}\)

Therefore, the square root of 36 is \( \pm 6\).

Square roots by estimation

In various cases, the perfect square root of a number doesn’t exist and we estimate the nearest value. This can be explained by taking the example of 24.

1. Start by finding the nearest perfect squares to 24. These are 25 and 16, whose square roots are 4 and 5.
2. Since \({5^2}\)  is closer to 24, we increase 4 to 4.5 and check again.
3. Again, \({4^2} = 20.25,So\;{5^2}\) is still closer to 24. We adjust again and go from 4.5 to 4.8.
4. This way, we continue till a close enough estimate has been made. In this case, it comes out to be 4.8989

Also read: How to Find Cube Root of a Number

Square roots by Long division method

It is a method used to find the square roots of large numbers by dividing them into parts and getting the exact value of the square root of the number.

Example: Find the square root of 150 using the long division method?

To obtain the square root of a number using long division:

1. Group the digits of the number into pairs starting from the rightmost digit. This is done by placing bars on top of the groups for easy identification.
2. Find the largest perfect square less than or equal to the leftmost pair (which is 1 here) and use its square root as the divisor and quotient (both come out to be 1). Divide the leftmost pair (1 here) by the divisor, and bring down the next pair of digits (50 here). 
3. Bring the last digit of the quotient (1 here) to the divisor (1 again) and using the sum of these two numbers (1+1=2). Now try to find the largest two digit number that starts with 2 and doubling which, will give us a number below the number we have brought down (50 here).
4. Continue the process in this way and add a decimal point in the quotient and zeroes in the dividend if required untill a desired accuracy is reached. The final quotient will become our square root.

The following table better demonstrates this:

Hence, the square root of 150 is equal to 12.247

Solved Examples

1. Find the square root of 144 via prime factorization.

When we factorise 144, we arrive at the following equation

\(144 = 2 \times 2 \times 2 \times 2 \times 3 \times 3\)

We group these factors into pairs

\(144 = \left( {2 \times 2} \right) \times \left( {2 \times 2} \right) \times \left( {3 \times 3} \right)\)

Then take one factor from each pair.

\(144 = 2 \times 2 \times 3\)

Hence, 12 is the square root of 144.

2. Estimate the square root of 30.

The nearest perfect squares are 25 and 36 and therefore, the square root of 30 must lie between 5 and 6. Since \({5.5^2} = 30.25\), the square root of 30 is very close to 5.5. We now try the guess 5.4, whose square is 29.16. To get better accuracy, let us go up to 5.45, whose square is 29.7025. Continuing this way, we get the desired answer as 5.4772.

Summary

This article discussed the following concepts:

1. What is meant by the square and square root of a number?
2. How square roots are represented.
3. Various ways of finding square roots of a number. These included prime factorization, estimation, and long division methods.

 

Frequently Asked Questions

1.What are the methods used in finding the square root of a decimal number?

The square root of a decimal number may be found via long-division or estimation methods.

2. When is prime factorization useful?

Prime factorization is only useful when the given number is a perfect square. Otherwise, it fails.

3. What are perfect squares?

Perfect squares are those numbers whose square roots are whole numbers, rather than decimal numbers.

4. How do we find square roots of numbers which aren’t perfect squares?

Estimation and long division methods can aid us in such scenarios.