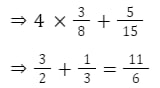Blog

Introduction

The Khalji dynasty reigned during the height of the Delhi sultanate, and Allaudin Khalji was credited with most of its accomplishments. He united the entire Indian subcontinent under his reign and was the most powerful sultan of the Delhi sultanate. After slaying his father-in-law Jalaluddin Khalji, the founder of the dynasty, Alauddin Khalji ascended to the throne in 1296. In 1320, the Ghiiyasuddin Tughluq overthrew the Khalji dynasty and established the Tughlaq dynasty. Later, Mohammad Tughluq oversaw the growth of the Sultanate.

Consolidation under Khalji Dynasty

Due to internal strife among the noles, Jalaluddin, the first king of the Khalji dynasty, was unable to extend his territory. He had a brief six-year reign during which he spent time stabilising and legitimising his position and power. Alauddin Khalji, Jalaluddin’s son-in-law, killed him, took the throne for himself, and proclaimed himself the ruler of the Delhi sultanate.

The Delhi Sultanate reached its pinnacle under Alauddin Khalji. Alauddin’s first trip was to Gujrat in 1299. This was his first foray into new territory. He stole the wealth and appointed Alp Khan governor. He continued his westward expansion by attacking Malwa in 1305 and winning a bloody struggle to take the fort of Mandu. He seized control of Chittor, Mewar, and Ranthambore as well as all of western India. Alauddin extended his hegemony into southern India. Wherever he triumphed, he appointed his trusted nobles as administrators.

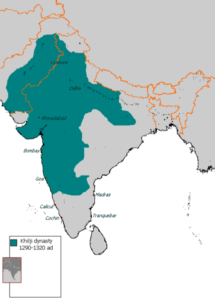
Administration under the Khalji Dynasty:

The kings of the Khalji people appointed their military leaders as governors and gave them authority over their territory. These territories were referred to as “Iqta” and the owners as “Iqtadar” or “Muqti.” Iqtadars were required to support the king militarily and uphold law and order in their region. Iqtadar received a wage from the money their territories generated. Three different tax types existed. The first tax was imposed on the “kharaj” portion of the crop, followed by a tax on cattle and a third tax on horses. Throughout Alauddin Khalji’s reign, numerous administrative changes were made.

• The empire was divided into provinces, and there were 11 provinces under Alauddin Khan.
• Alauddin established a sizable standing army to defend the country from Mongol intrusion.
• For his troops, Alauddin built the garrison town of Siri.
• He also levied taxes in the Ganga Yamuna doab region to pay for the rations of his soldiers. He set the prices for goods in Delhi; government employees were assigned to monitor this, and those who failed to sell at the set price faced consequences.
• The first emperor to pay his troops in cash was Alauddin. Alauddin had managed the market price so that it stayed constant even during the Mongol invasion.

Consolidation under Tughlaq Dynasty:

The Deccan Sultanate’s rule was not unbreakable; with the death of Alauddin, the southern provinces rose up and gained their independence. The founder of the Tughlaq dynasty, Ghyisuddin Tughluq, was made aware of this. During the brief period of his administration, Ghiyasuddin was unable to subjugate the south to the Delhi sultanate. After assuming power, Mohammad bin Tughluq concentrated his effort on the south. He organised numerous military operations and seized control of a sizable portion of the South.

He went on to Mabar in the south. He conquered Bengal in the east, which had declared itself independent because of its separation from the Delhi sultanate and the difficulty of maintaining administration and consolidation at such a distance.

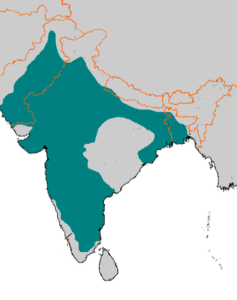
Mohammad Tughluq organised a number of far north and northwest missions. After suffering a severe defeat in Tibet with his troops, he planned the Qurachi expedition but later abandoned it. The Delhi Sultanate’s largest domain belonged to Mohammad Tughluq, and this contributed to the sultanate’s demise.

Administration under Tughlaq Dynasty:

The Tughlaq dynasty preserved the empire while carrying out the majority of Khalji’s administrative principles. Nobles were given the authority to collect taxes from their iqta as part of the tradition of iqta. Bandagan continued to be appointed as governor and military commander under Tughlaqs. Specially trained slaves called bandagan were loyal only to the King. Some rules imposed by the king were highly controversial. He appointed gardeners, cooks, and wine distillers to high administrative posts at once. The noles were harshly critical of the ruler’s unorthodox methods.

• To stop the Mongols from capturing their empire, Mohammad established a powerful standing army.
• His victory over the Mongol invasion. Instead of building a new garrison town for the army, he dispersed its population to Daulatabad and stationed his soldiers in an old Delhi neighbourhood.
• Taxes were raised to provide for the troops.
• People started to feel unsatisfied as a result.
• At the same period, north India had a famine.
• His attempt at token currency, which was made of cheap metal and was simple to reproduce, failed horribly.
• Taxes were paid with token money, and gold was kept.

Summary

The Khalji and Tughlaq dynasties represented the height of the Delhi sultanate. The Khalji monarch Alauddin implemented strict laws and regulations to manage his enormous realm. He was an astute administrator who worked hard to keep Delhi’s commodity prices stable. The Tughlaq dynasty inherited Khalji’s administrative and expansionist objectives. Mohammad Tuhghluq, the most well-known king of Tughlaq, introduced many radically new administrative reforms and conducted numerous policy experiments. Unfortunately, he had short-sighted policies and was a hasty and irritable ruler, which led to the slow decline of his kingdom.

Frequently Asked Questions

1.What were Muqtis’ Responsibilities?
Ans. Muqties were required to uphold peace and order in their iqtas as well as provide the emperor with military support. Muqties were permitted to deduct taxes from his iqta in exchange for their services.

2.Who were the Chieftains?
Ans. Chieftains were another name for Samanta nobility. They were wealthy landowners who lived in the countryside, and the empire brought them under its control and taxed them.

3.What is Accurate in terms of Governance and Unification under the Khaljis and Tughlaqs?
Ans. Even though these dynasties ruled over the majority of the Indian subcontinent, most of the interior remained independent. The hardest part of managing all the provinces was the distance, and remote areas like Bengal were tough to manage.

Introduction

The relationship between two expressions on either side of the equal to sign is represented by an equation in mathematics. One equal symbol and one variable are used in this kind of equation. Simple equations use arithmetic operations to balance the expressions.

A simple equation is an equation that shows the relationship between two expressions on both sides of the sign. Only one variable appears in these kinds of equations, either on the first side or the other side of the equal symbol. For instance, 83 = 5 – 4z. In the provided example, the variable is z. Simple equations use arithmetic operations to balance the expressions on both sides. Linear equations in one variable are also regarded as simple equations.

Equations

Equations are relationships between two or more expressions connected by the equals sign, or “=.” Variables, coefficients, and constants are the three components of an equation.

Variables: Variables are the names given to the symbols (typically English alphabets) that are assigned to an arbitrary, unknowable value.

Coefficients: The coefficients of a term are the numbers that are multiplied by a variable or the product of two variables in that term.

Constants: Constants are the numbers that are independent of variables.

Simple Equations

A type of equation known as a simple equation compares two linear expressions with just one variable in common. Several instances of basic/simple equations are

3x + 4 = 7

4x + 5 = 3x + 8

Since many of the situations, we encounter in real life can be formulated as simple equation problems, we can use simple equations to obtain the desired results in a variety of areas of life.

Simple Equations questions

Simple equation problems, which can be represented by a simple equation to find the value of something unknown based on some given conditions, are known as simple equation questions. One such example of applying simple equations to real-world situations is provided, 

Let’s say Amar and Bipin, two friends, are purchasing apples. Amar might have purchased 5 kg and Bipin 3 kg. If Amar paid Rs. 80 more than Bipin, we must determine the cost of a kg of apples. The following simple equation can be used to represent this situation:

5x = 3x + 80, where x is the price of 1 kg apples.

Solving Simple Equations

To answer questions involving simple equations, we change the equation so that the term with the variables is on one side of the equation and the term with constants is on the other. We then simplify both sides so that there is only one term on each side, one with variables and the other with constants.

The value of the variable is then obtained by simply multiplying the equation by the reciprocal of the coefficient.

Now, let’s look at some examples to help us better understand it.

Example: Solve the following simple equation, 5x – 20 = 3x + 60

Solution: Here we have 5x – 20 = 3x + 60

Adding 20 to both sides while subtracting 3x to move terms with variables to one side and constants to the other.

⇒ 5x – 20 + 20 – 3x = 3x + 60 + 20 – 3x

⇒ 5x – 3x = 60 + 20

⇒ 2x = 80

Dividing by 2 on both sides

⇒ x = 40

Simple Equation Problems

Simple equation problems are mathematical issues from the real world that are modelled by simple equations. We must first determine the number of arbitrary values present and their relationships to represent a given situation using a simple equation. If there is only one arbitrary value, it is easy to create a simple equation to describe it; however, if there are several arbitrary values, we must establish a direct relationship between them to do so.

Example: Determine whether the following scenario can be modelled as a simple equation or not. Amit is currently twice as older than his younger brother Sagar. The combined age of Amit and Sagar was 23, two years ago. Identify their current ages.

Solution: Since Amit’s age and Sagar’s age are arbitrary values, the only way we can depict this situation in a simple equation is if there is a direct correlation between their ages, which is implied by the first statement that Amit is currently twice as old as Sagar. As a result, we can express this as a simple equation problem.

Let Sagar’s present age be x years

And Amit’s present age be y years

Then, ATQ

In present, y = 2x

Also, two years ago, (x – 2) + (y – 2) = 23

Substituting y = 2x in the second equation,

⇒ x – 2 + 2x – 2 = 23

Equations in Everyday Life Examples

When a value for a quantity or identity is unknown in a real-world situation and cannot be determined by a simple mathematical operation, linear equations are used, such as when estimating future income, forecasting future profits, or figuring out mileage rates.

Here are a few real-world instances where applications of linear equations are used.

• Can be used to identify age-related problems.
• It is used to determine the distance, duration, and speed of a moving object.
• It is used to resolve problems involving money, percentages, etc.

Solved Examples

Example: Calculate the value of y from the equation:  – 5 = 6.

Solution: We will simplify the equation first by separating the variables and constants,

– 5 = 6

Add 5 on both sides,

⇒  – 5 + 5 = 6 + 5

⇒  = 11

Multiply by 3 on both sides,

⇒  x 3 = 11 x 3

⇒ 11y = 33

Divide by 11 on both sides,

⇒ y = 3

Summary

Simple equations are also known as linear equations when they contain multiple variables and can be resolved using a variety of techniques. To solve problems from daily life, such as how to measure an unknown length, etc., we use simple equations. The typical method of representing the relationship between variables is through simple equations. A simple equation is a linear equation that only has one variable. Simple equations were credited to Rene Descartes as their creator. One of the foundations of algebra is simple equations.

Frequently Asked Questions (FAQs)

1. What are Linear Equations?

Linear equations are the mathematical relations that relate two expressions of degree 1 with the equal to symbol.

2. What are Simple Equations?

Simple equations are linear equations that have only one variable. Simple equations can be solved easily and are very useful in many days to day life problems.

3. What are the different methods of Solving Simple Equations?

There are two ways that we can solve simple equations. The techniques are the systematic method and the trial-and-error method.

4. What is a Rational Expression?

A rational expression is expressed in terms of the fraction of two algebraic expressions, and it also belongs to the class of simple equations.

Introduction

Natural numbers, their additive inverses, and zero are all collectively known as a set of integers. We get a whole number when we subtract a small number from a larger number. However, there are no whole numbers that can represent the difference between a large number and a smaller number, such as 12 – 37. We created integers to describe such differences. Integer Addition follows all the rules of algebra, whereas integer subtraction doesn’t.

Division of Integers

We can use the properties of integer division because we are accustomed to working with whole numbers and natural numbers. 

The Division of Integers rules:

Rule 1: A positive integer is always the quotient of two positive integers or two negative integers.

Rule 2: A positive integer’s quotient when divided by a negative integer is always negative.

One important thing to keep in mind is that you should always divide without signs, but once you have the integer solution, give the sign following the sign specified in the problem.

Learn More about Properties of Division of Integers. Check out more videos in Maths Class 7 Lesson no 01.

Properties of Integer Operations

Integers have a few properties that govern how they operate. These principles or properties can be used to solve a wide range of equations. Integers are any positive or negative number, including zero, to refresh your memory. These integers’ properties will aid in quickly simplifying and answering a series of integer operations.

All addition, subtraction, multiplication, and division properties and identities apply to all integers. The set of positive, zero, and negative numbers represented by the letter Z is known as an integer. Integers have the following five operational properties:

• Closure Property
• Commutative Property
• Associative Property
• Distributive Property
• Identity Property

Closure Property

According to the closure property, the set of all integers is closed under addition and multiplication, i.e., addition or multiplication of any two integers will always result in an integer. Subtraction of integers also follows the closure property; division however does not follow the same rule for integers.

If a and b are two integers, then if,

c = a + b and d = a × b

Then both c and d are also integers.

But r = a/b is not always an integer.

Thus, the division of integers is not always closed.

Commutative Property

According to the commutative property of addition and multiplication, the order of terms does not affect the result. Let a and b be two integers, then by the commutative law:

a + b = b + a

Also,

a x b = b x a

But subtraction and Division do not follow the same rules.

Associative Property

According to the associative property of addition and multiplication, it doesn’t matter how numbers are grouped; the result is the same. Regardless of the order of the terms, parenthesis can be used.

a + (b + c) = (a + b) + c

Also,

a × (b × c) = (a × b) × c

However, again subtraction and Division are not associative for Integers.

Distributive Property

The distributive property explains how one mathematical operation can distribute over another within a bracket. To make the calculations easier, the distributive property of addition or the distributive property of subtraction could be used. In this case, integers are multiplied or divided by each number in the bracket before being added or subtracted again.

Multiplication is distributive from both sides, but Division is distributive only from the right side (denominator/divisor)

(a ± b) ÷ c = (a ÷ c) ± (b ÷ c)

Identity Property

When any integer is added to zero no matter the order, the result is the same number, according to the additive identity property of integers. Zero is known as additive identity.

Let a be an integer

Then, since 0 is known as additive identity

a + 0 = a = 0 + a

Similar to this, we have the multiplicative identity. When a number is multiplied by 1 in any order, the product is the integer itself, according to the multiplicative identity property for integers.

Again, let a be an integer,

Then, since 1 is known as the multiplicative identity

a × 1 = a = 1 × a

Again, like most other properties, subtraction and division do not follow the identity property.

BODMAS Rule

To simplify the calculations of more than two numbers having several types of operators, we have formed a rule that governs how to put parentheses around certain terms when solving the parentheses from the centre simplifies the calculation a lot.

This rule goes like

Bracket Of Division Multiplication Addition Subtraction – BODMAS

Here in this definition the ‘Of’ stands for functions such as exponents or square roots. So according to this rule, we put the centre of parentheses or brackets on subtraction, then addition, then multiplication and then division leaving the functions outside.

Solved Examples

Example: Are the following Integer operations closed (have an Integer result)?

a.  2 + 3/ (5 – 2)

b.  4(3/8) + 5/15

Solution:

a.  2 + 3/ (5 – 2)

Using BODMAS, we will simplify the terms by solving within the parentheses first.

⇒ 2 + 3/ (3)

⇒ 2 + 1 = 3

This operation is closed.

b.  4(3/8) + 5/15

Using BODMAS, we will simplify the terms by solving within the parentheses first.

This operation is not closed.

Also Read: Properties of Addition and Subtraction of Integers

Summary

This article discusses the topic of Integers, Integer Division. While also shining a light on the properties of Integers operations such as closure property, commutative property, etc. Integer division however does not follow most of these properties.

FAQs

 1. What are Integers? How are they different from other types of numbers, such as natural numbers and whole numbers?
Ans. Integers are numbers that have no decimal value, they are represented by whole values. The integers contain both positive and negative numbers along with the number 0. The positive integers are known as natural numbers, whereas the positive integers with 0, aka the non-negative integers, are known as whole numbers.

2. What are the rules for Dividing Integers?
Ans. The division of integers follows two simple rules,

1. Dividing two integers of the same sign results in the quotient of the value of those numbers and the result has a positive sign.
2. Dividing two integers of different signs results in the quotient of the value of integers and the result has a negative sign.

3. Which is the only Property of Integer Operations that Division follows, and on What Condition?
Ans. The distributive property is the only property of integer operations that the division of integers follows, and it follows the distributive property only from the right-hand side.

Introduction

Although factors and multiples are entirely different concepts, they are related. To determine the factors, we divide the given number by another number, whereas multiples of the given number can be obtained by multiplying the given number by any other number. Multiplication is involved in both ideas. To obtain a given number, we multiply two numbers; the two numbers we multiplied are referred to as the obtained number’s factors.

For example, 4 x 5 = 20. Therefore, 20 is a multiple of 4 and 5, and 4 and 5 are factors of 20.

The number that is the factor of two or more numbers is referred to as the common factor. GCD (Greatest Common Divisor) and HCF (Highest Common Factor) are terms that relate to this idea.

The common multiple is the number that is a multiple of two or more other numbers. The Least Common Multiple, or LCM, is related to this idea. Different divisibility criteria can be used to determine whether a given number is divisible by another without actually conducting the division operation.

Factors

A number must divide completely, leaving no remainder, to be the factor of any other number. In other words, we can also say that the divisor is a factor of the dividend if a number (the dividend) is exactly divisible by any other number (the divisor), leaving no remainder.

For Example: Let’s take the number 36, if we check for factors of 36, we have

36 = 1 x 36 = 2 x 18 = 3 x 12 = 4 x 9 = 6 x 6

Properties of Factors

• If a division of a number by another number leaves no remainder, then that second number is said to be the factor of the first number.
• A number can only have a finite number of factors.
• Prime numbers are those that only have themselves and the number 1 as factors.
• Composite numbers are those that have more than two factors.
• Finding a number’s factors involves using division.
• The obtained factors are always less than the initial number.

Multiples

Multiples are numbers created by multiplying the given number by integers. The multiplication table shows the multiples of a given number.

Properties of Multiples

• The results of multiplying an integer by a given number are referred to as the given number’s multiples.
• There are an infinite number of multiples of a number.
• Finding a number’s multiples requires the use of multiplication.
• The multiples of a given number exceed or are equal to that number.
• Every number is a multiple of itself.

Difference between Factors and Multiples

Some differences between factors and multiples are given in the table below:

Factors	Multiples
Factors are exact divisors of a number.	Multiple has the number as its exact divisor.
Factors of a number are finite.	Multiples of a number are infinite.
Factors are obtained by division.	Multiples are obtained by multiplication.
Factors of a number are always less than or equal to the number itself.	Multiples of a number are always greater than or equal to the number itself.

Common Factors and HCF

A common factor is any factor that two or more numbers share.

For example, take 35 and 42

Factors of 35 = 1, 5, 7, 35

Factors of 42 = 1, 2, 3, 6, 7, 14, 21, 42

Both 35 and 42 have some factors such as 1 and 7 that are common to both, these are known as common factors of 35 and 42.

Now, in this case in the list of common factors, 7 is the largest number, or we can also call it the highest common factor, i.e., HCF.

Thus, HCF or the highest common factor of a set of numbers is defined as the largest number that divides all the numbers in the given set of numbers.

Common Multiples and LCM.

Common multiples are those multiples that are shared by two or more different numbers.

For example, take 6 and 8

Some multiples of 6 are, 6, 12, 18, 24, 30, 36, 42, 48, 54, 60 etc.

Some multiples of 8 are 8, 16, 24, 32, 40, 48, 56, 64, 72, 80 etc.

Here, both 6 and 8 share some common multiples such as 24, 48 and infinitely many more. These are known as common multiples of 6 and 8.

In this case, in the list of common multiples, 24 is the smallest, or we can also call it the least common multiple, i.e., LCM.

Thus, LCM or least common multiple of a set of numbers is defined as the smallest number that is a multiple of or is divisible by all the numbers in the given set of numbers.

Solved Examples

Question: Find the list of factors of 36.

Solution: We know that 1 and the number itself, i.e., 36, are the two trivial factors, so we will start dividing by the next number.

36 ÷ 2 = 18, Thus, 2 and 18 are two more factors of 36, moving to the next number

36 ÷ 3 = 12, Thus, 3 and 12 are two more factors of 36, moving to the next number

36 ÷ 4 = 9, Thus, 4 and 9 are two more factors of 36, moving to the next number

Clearly, 36 is not divisible by 5 since it doesn’t have 5 or 0 in the unit place, moving to the next number

36 ÷ 6 = 6, Thus, 6 is the final factor of 36.

Factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18, and 36.

Summary

This article provides insight into the topic of Factors and Multiples, while also shining a light on the concept of common factors and common multiples. To completely divide another number without leaving any remainder, a number must be the factor of that other number. The multiples are the results of multiplying the given number by integers. Common multiples are those multiples that are shared by two or more different numbers. A common factor exists for two or more different numbers.

Frequently Asked Questions (FAQs)

1. What are Factors and Multiples?

Ans. Factors of a number are defined as the number that divides the given number completely and evenly without leaving any remainder.

Multiples on the other hand are the numbers obtained by multiplying the given number by different integers.

2. What are Prime Numbers?

Ans. Prime numbers are defined as numbers greater than 1 that have only 2 factors, i.e., 1 and the number itself. Some examples of prime numbers are 2, 3, 5, 7, 11, etc.

3. What is the Fundamental Theorem of Arithmetic?

Ans. The fundamental theorem of arithmetic states that every number can be broken into the product of some prime numbers, also known as its prime factors. This product is unique to a number and cannot ever change no matter how you find it, only the order of the product changes.

4. What is the Relationship between HCF and LCM of two Numbers?

Ans. The relationship between is defined as: The product of HCF and LCM of two numbers is equal to the product of the two numbers.

HCF (a, b) × LCM (a, b) = a × b

Introduction

The ability to work emanates with energy. For any action, we require energy in the form of mechanical, chemical, electrical, static, kinetic, muscular, and other forms. Understanding the several energy sources is necessary for utilising all forms of energy, which can be obtained from various sources, including both natural and artificial ones. Interestingly, natural energy sources include the sun, wind, tidal, geothermal, and gravitational energies, while artificial energy sources include biomass, coal, petroleum, and a host of others. To ensure that the energy resources survive for a long time, it is crucial to save and use them as effectively as possible. Although not all energy sources release dangerous gases, their use can occasionally lead to pollution. Moreover, energy comes in two forms: traditional and unconventional sources.

Conventional Sources of Energy

Conventional energy sources are non-renewable, which implies that after they have been utilised, they cannot be reused. Coal, oil, natural gas, fuel wood, and nuclear energy are a few examples of traditional/conventional sources of energy. Coal, natural gas, and petroleum account for 90% of the commercial energy produced worldwide, while nuclear power accounts only for 10%.

Types of Conventional Sources of Energy

a. Coal

• Coal, a sedimentary rock in the black-brown range, is the most prevalent conventional energy source and has a long lifespan of 200 years. Long-term exposure to heat and pressure transforms dead plants into lignite and anthracite, which are then finally transformed into coal.
• There are several applications for coal, such as fuel for steam engines in trains and the production of electricity.
• About 70% of the total energy used in our nation is generated by coal.

b. Oil

• Due to the variety of uses for oil, it is one of the most significant conventional energy sources.
• The oil extraction procedure, which entails several processes, is used to obtain the oil.
• Oil is utilised commercially and in a variety of sectors, including the food, cosmetic, and transportation industries.

c. Petroleum and Natural Gas

• Petroleum is made up of Alkanes and cycloalkanes.
• Methane, ethane, propane, butane, and hydrogen sulphide are all components of natural gas.
• Natural gas is created when gas comes into contact with the petroleum layer and is a black liquid when it is in its raw state.
• Petroleum is used to make things like plastic, petrol, and diesel.
• Compared to other fuels, natural gas produces less air pollution.

d. Nuclear Energy

• Nuclear materials that contain radioactive elements are used to create energy.
• 300 or more nuclear reactions are required for the production of nuclear energy.
• Some negative effects of nuclear energy include its radioactivity and danger.
• From one location to another, it is simple to travel by rail or ship. For instance, coal, oil, and natural gas are raw materials.

Advantages of Conventional Sources of Energy

• For any energy, the installation of conventional plants is simple.
• There is no need to wait for energy to be generated because it may be produced quickly depending on the needs.
• Alternative forms of energy are readily accessible and renewable resources that may be utilised again.
• Solar energy, wind energy, tidal energy, geothermal energy, biomass, and solar energy are a few examples of non-conventional sources.

Non-conventional Sources of Energy 

• Alternative forms of energy are readily accessible and renewable resources that may be utilised again.
• Solar energy, wind energy, tidal energy, geothermal energy, biomass, and solar energy are a few examples of non-conventional sources.

Solar Energy

• In solar power plants, sunlight is transformed into electrical energy to produce solar energy.
• Although solar energy is the most significant non-conventional energy source, it is also the least consumed.
• Solar energy comes from renewable resources, is widely accessible, and is non-polluting. 
• Solar ovens, solar panels, solar heaters, and solar cells are a few examples.

Wind Energy

• Turbines are used to generate electricity from wind as a source of energy.
• The power output rises along with the wind speed.
• These wind turbines are situated where the wind speed is strongest and at its highest altitude.
• Wind energy is positioned close to agricultural regions and is pollution-free.

Biomass Energy

• Wood, sewage, plants, animals, and other organic materials are used to create biomass.
• Burning this material releases heat energy, which is then transformed into electrical energy.
• Cooking, lighting, and the production of power are among the uses of biomass.
• A total of 14% of the world’s energy comes from biomass.

Tidal Energy

• Tidal energy is produced by turning the mechanical energy of tides into electricity.
• This energy source can be used in areas that are close to oceans and seas.

Advantages of Non-Conventional Sources of Energy

• These resources are very less expensive and renewable.
• Non-conventional sources are environmentally friendly.
• These resources require low maintenance.
• Offer long-term use as compared to conventional sources.

A comparison between the Conventional and Non-Conventional Sources of Energy.

Conventional Source of Energy	Non-Conventional Source of Energy
Conventional sources of Energy is being used for a longer period.	Non-conventional energy sources have lately been created and are environmentally beneficial.
Conventional resources are a prominent cause of environmental pollution due to the emission of gases and smoke.	Since non-conventional energy is derived from renewable
Non-renewable sources of energy.	Renewable sources of energy.
Examples – Coal, Petroleum, Natural Gas, oil, and Nuclear Energy.	Examples-Wind Energy, Solar Energy, Tidal Energy, Hydropower Energy, and Thermal Energy.

Summary

Conventional sources of energy emit greenhouse gases while producing power and are limited, therefore then-conventional energy sources, which are renewable and environmentally favourable are suitable for sustainability. The major conventional energy sources are coal, oil, petroleum, natural gases, etc. while the non-conventional sources include solar energy, wind energy, tidal energy, biomass energy, etc.

Frequently Asked Questions

1. Why should we Conserve Energy?

Ans: Energy conservation is a measure used to protect and preserve energy sources from becoming extinct. We must save our energy supplies for later use. Utilisation must be reduced to conserve. Our needs are growing daily, yet we only have a limited amount of energy resources. 

2. What is a Renewable Source of Energy?

Ans. Renewable energy comes from naturally occurring, regenerative sources. Renewable energy sources include wind, solar, biomass, thermal, etc. Renewable energy can be continuously replenished without running out.

About 16% of the world’s energy consumption is made up of renewable sources. Renewable energy is a plentiful and sustainable source of power. Sunlight is the most significant and widely available renewable energy source.

3. What are the Advantages of Non-Conventional Sources of Energy over Conventional Sources of Energy?

Ans. The natural limitations of conventional energy sources, which emerged after millions of years and are subject to extinction at any time, make them very vulnerable. The abundance of non-traditional energy sources in nature makes them increasingly significant and practical. Additionally, non-traditional sources of energy are environmentally beneficial and don’t damage or contaminate the environment. The cost of fuel generated from unconventional energy sources is lower than that of traditional energy sources.

Introduction

Every day, new technological components are developed as technology advances throughout the globe. Electricity powers every other home, public space, and industry. People utilise electricity, and they use it for a variety of things. But how is it that this electric current has a particular level of power and continues to flow without any breaks? It is done with the aid of an object known as a conductor. Electric current may readily flow via the conductor. A conductor is built into anything that uses electricity to operate. These currents produce forces that flow in one direction. Let’s discover more about it.

Current Carrying Conductor 

A conductor that is transporting current can withstand the current’s force. Each current has a specific voltage that defines the electrical power. Electric bulbs can burst at high voltage, whereas low voltage results in weak electric current. There is no electric field surrounding the conductors. Unless a charge or electric field is given to it, it is neutral. The conductor’s sole responsibility is to transmit the current uninterruptedly to each source.

Magnetic Field due to Current Carrying Conductor.

A conductor that is conducting current generates a magnetic field everywhere around it. A current, as we all know, is a net charge that moves across a medium. The presence of moving charges in a conductor is a prerequisite for the creation of magnetic fields. Due to the magnetic fields‘ extra charge, an electric field is created. All of these elements help the current flow through a conductor smoothly.

Force on a Current Carrying Conductor in a Magnetic Field

A conductor experiences forces because of the external magnetic field. When two magnetic fields interact, there will be attraction and repulsion (according to their properties) based on the direction of the magnetic field and the direction of the current. That’s how a conductor experiences force. This phenomenon is termed Magnetic Lorentz force. This was found by H. A. Lorentz. This force is perpendicular to the direction of the charge and also to the direction of the magnetic field. It is a vector combination of the two forces.

The equation of the force on a conductor having a charge q and moving through a magnetic field strength of B is given as,

F = qvBsinθ

This equation can also be written as,

Where L is the length of the wire and t is the time. Rearranging the above equation, we get,

The Direction of a Force in a Magnetic Field

It is believed that the force acts perpendicular to the current’s direction. The left-hand rule is used to accomplish this. John Ambrose Fleming established this regulation. It is important to remember that the magnetic force is orthogonal to both the direction of motion and the charge velocity. Understanding which direction is applied to it is made easier by the left-hand rule.

State The Rule to Determine the Force or Direction

The direction of force, as we have seen in the article above, is perpendicular to both the magnetic field and the direction of the current. And the Right-hand rule-I decides this. The best mnemonic to remember the direction of force and current flow through the right hand is this example. The details are as follows:

• Place a hand between the magnetic field.
• The direction of the thumb points to the direction of the current (I).
• The fingers are facing the direction of the magnetic field (B).
• Now, the palm is facing the direction of the force (F).

Fleming’s Left-Hand Rule Definition

The current-carrying conductor will feel a force that is perpendicular to both the direction of the current and the magnetic field if it is put in the external magnetic field, according to a rule developed by John Ambrose Fleming. According to Fleming’s Left-Hand Rule, the thumb points in the direction of magnetic force, the forefinger points in the direction of the magnetic field, and the middle finger points in the direction of current if our forefinger, middle finger, and thumb are positioned perpendicular to one another. The late 19th century saw the development of this regulation.

Summary

Conductors have moving charges that are required for the magnetic field. Force moves in a perpendicular direction to the magnetic field and electric current. The magnetic field also exerts equal and opposite force in the current-carrying conductor.

Frequently Asked Questions

1. What is an Insulator?

Ans: We are aware that conductors enable uninterrupted electric current flow through them. However, it may also be prevented from flowing. Insulators carry out the work. Insulators are regarded as poor conductors of electricity because they do not permit electrons or atoms of materials to travel through them. Additionally, insulators have high resistance. Insulators still have some electric charge even if they prevent current passage. As a result, its primary use is high voltage resistance. Some examples are non-metals.

2. What are some High-Conduction Metals?

Ans: Metals that conduct heat and electricity in a very efficient way are called high-conduction metals, such that of gold, silver, and copper. In these materials copper is for construction purposes, making wires, cables, motors etc. because it’s cheaper than gold and silver. However, gold is used at very specific places due to its cost, and it is robust to environmental hazards like sulphur, oxygen, and water, whereas silver and copper react with environmental hazards.

3. What is a Semiconductor?

Ans: Semiconductors are materials that combine conductivity and insulator properties. Due to their capacity to both deliver and resist current flow, semiconductors are primarily employed in the production of electronic products and equipment. Doping the impurities into the crystal’s structure can change them. Silicon and gallium arsenide are two common semiconductors.

Introduction

H.C. Oersted discovered the magnetic effect surrounding the current-carrying conductor in the 19th century. The region around a magnet or current-carrying conductor where another object feels a magnetic force caused by the magnet or current-carrying body is known as the magnetic field. A current-carrying conductor creates a magnetic field all around it homogeneously due to the flow of current-carrying electrons, which generates a magnetic field, and its magnitude is proportional to the current in the conductor. Therefore, the distance from the current-carrying conductor and the total current in the wire control the magnetic force felt by any object near the current-carrying conductor.

What is a Magnetic Field?

An invisible field called a magnetic field surrounds a magnet or a magnetic substance. The magnetic force operates in this field. Other magnetic objects can be drawn into or pushed away from this field by this magnetic force. A magnetic field develops when electrons move in a certain direction having a negative charge. A magnetic field can be represented by drawing magnetic field lines that are continuous lines originating from the north pole of the magnet and migrating towards the south forming continuous loops. Inside a magnet, this orientation is the opposite.

Magnetic Field due to Current Carrying Conductor

We are aware that stationary charges generate an electric field whose strength is proportional to the charge. The same theory may be used in this situation. Moving charges generate a magnetic field proportional to the strength of the current, which causes the conductor carrying the current to generate a magnetic field everywhere around it. Electrons are responsible for producing this magnetic field. Due to its magnitude and direction, the magnetic field can be considered a vector quantity. The magnetic field’s direction is parallel to the wire’s length. It may be provided using the right-hand thumb rule. According to this rule, if we grasp the conductor carrying the current in our right hand and point our thumb in the direction of the current, our curled fingers will point in the direction of the magnetic field lines. This is seen in the diagram below.

Magnetic Field due to a Current-Carrying Wire

Consider a current carrying wire having a current I, then the magnetic field strength B, at a distance r from the wire can be estimated using the formula such that, 

The direction of the produced magnetic field due to a current-carrying wire is estimated with the help of the right-hand thumb rule, as shown in the below figure.

Magnetic Force on a Current-Carrying Wire

The equation of the force on a conductor having a charge q and moving through a magnetic field strength of B is given as,

F = qvBsinθ

This equation can also be written as,

F =

Where L is the length of the wire and t is the time. Rearranging the above equation, we get,

Relation between the Current and Magnetic Field 

The relation between current and magnetic field is given by Biot Savart’s Law, such that,

Summary

A magnetic field can be created when electrons moving in a certain direction have a negative charge. An invisible field called a magnetic field surrounds a magnet or a magnetic substance. The magnetic force operates in this field. The relationship between the magnetic field and current strength is direct.

Frequently Asked Questions (FAQs)

1. What is the law of Biot Savart?

Ans: By this law, the magnetic field generated due to a small current-carrying element depends upon the square of the distance between the point and the current-carrying element, the magnitude of the current, the length of the current element, and the sine of the angle formed by the current’s direction and the line connecting it. This law is comparable to Coulomb’s law in electrostatics. The vector quantity is represented by this element.

2. What is the Right-Hand Rule of Fleming?

Ans: When our thumb, index finger, and middle finger are arranged so that they are all perpendicular to one another, this law states that the thumb indicates the direction of the conductor’s motion, the middle finger gives the direction of the current induced, and the index finger gives the direction of the magnetic field. Fleming’s Right-Hand Rule determines the direction of the current that develops when a conductor moves through a magnetic field. This principle is utilised in electrical generators.

3. How Current Produces a Magnetic Field?

Ans: Ampere recognized that whenever an electrical charge is moving, a magnetic field is created. Similar to how an electrical current passing through a wire creates a magnetic field, the spinning, and circling of an atom’s nucleus accomplish the same. The magnetic field’s orientation is determined by the spin and orbit directions.

Introduction

When people think of algae, they typically picture slimy, green films that grow in still waterways (freshwater and marine). Depending on the species, an Alga may range in size from microscopic to macroscopic and up to a few feet long. Algae are the primary source of atmospheric oxygen that supports many life forms on earth while being blamed for ruining the beauty of transparent waters. The term phycology refers to the study of algae, and phycologists are those who conduct in-depth research on the organisms.

What is Algae?

Algae are cosmopolitan autotrophic eukaryotes having one or more cells that are capable of photosynthetic activity. Organelles like chloroplasts, mitochondria, and the nucleus are membrane-bound in algal cells. 

A common mistake students make is memorising Science or a process without understanding the concept behind it. Check out online study options are a great way to clear the science concepts you need. Watch the related video of these Science Concepts.

Examples of Algae

Some well-known algae include euglenoids, diatoms, kelps, Laminaria, Spirogyra, Volvox, Chara, Fucus, Micromonas, Noctaluca, Chilomonas, Gracilaria, and Chlamydomonas.

Characteristics of Algae

Algae can be multicellular or unicellular. They can also be microscopic as diatoms or large and leafy like kelp. They possess certain qualities that are essential for surviving in predetermined living circumstances.

Habitat: 

• The majority of algal species are found in freshwater and marine aquatic habitats. 
• Different types of water and temperatures allow algae to survive. 
• They can also grow on submerged surfaces and damp rocks. 

Morphology:

• Unlike plants, algae have a simple form. Unicellular algae can organise themselves into filaments or colonies and are either motile or non-motile.
• Kelp-like multicellular algae contain body features that are intended to serve particular purposes.

                                                

Interaction with Environment

Some algae can survive on their own (suspended in water or attached to the substrate), while some species coexist harmoniously with sponges, coral reefs, and fungi. 

Mode of nutrition:

• Chlorophyll is a pigment found in the majority of algae, which are photoautotrophs (photosynthetic pigment).
• The facultative and obligate heterotrophic algae are the only real exceptions. They need carbon substrates from their environment to survive. Some people think that algae exhibit mixotrophy (autotrophy and heterotrophy).

Reproduction

• Mitosis and fragmentation are used in vegetative reproduction. In fragmentation, the damaged component regenerates into a whole body. 
• Spore formation is the means of asexual reproduction. Mature cells divide and produce spores in their cytoplasm. Upon the emergence of favourable conditions, spores transform into new individuals. 
• Sexual reproduction is continued by gametes. Zygotes are created when male and female gametes combine. Female gametes can occasionally grow right into zygotes. This process is called parthenogenesis.

Classification of Algae

Based on their colours, distinct phyla of algae are subdivided. 

• Chlorophyta: Chlorophyll a and b, as well as carotenes, are the pigments found in chlorophyta (green algae). They can be found in colonies, multicellular forms, or unicellular forms. 
• Rhodophyta: Chlorophylls a and d, as well as phycoerythrin and phycocyanin, are the pigments found in Rhodophyta (red algae). They have a crimson appearance because of the phycoerythrin pigment. 
• Phaeophyta: Brown algae, or Phaeophyta, are pigmented with fucoxanthin and chlorophyll a and c. This category primarily includes kelps and seaweeds. 

Types of Algae

Depending on where they live, there are several forms of algae. 

• Cryophilic algae: Grow in snow and ice.
• Thermophilic algae: Grow in hot climates close to hot springs.
• Epizoic algae: Live on the bodies of aquatic creatures like turtles. 
• Edaphic algae: Grow in soil. 
• Epilithic algae: Grow on rocks. 
• Endolithic algae: Inhabit coral reefs. Some call it a symbiotic relationship.
• Corticolous algae: Grow on moist tree trunks.

Chemical Composition of Algae

They contain a variety of pigments, including fucoxanthin, carotenes, phycocyanins, and chlorophyll. Algae have significantly variable cell wall compositions. Cellulose, alginate, carrageenan, agarose, and glycoproteins, including galactans and mannans, are all parts of an algae’s cell wall. Other biomolecules found in algae include lipids, proteins, carbohydrates, nucleic acids (DNA since eukaryotes), and nucleic acids.

Difference between Normal Plants and Algae

Algae, like many sophisticated multicellular plants, use photosynthesis, which explains why chlorophyll is present. They don’t have genuine stems, leaves, or a clearly defined vascular system, which makes them different from plants.

Importance and Uses of Algae 

• They provide between 30 and 50 percent of the oxygen needed for other life forms on Earth. 
• Due to their abilities to gel, become colloidal, and create emulsions, red and brown algal extracts such as alginates, agar, and carrageenans are in high demand in the food sector. 
• Algae are quite sensitive to the condition of the water (pH and composition). They serve as bioindicators of environmental toxicity. 
• From algae that formerly inhabited sea floors, natural gas and crude oil are created. Nowadays, biofuel made from algae is more and more widespread.

Difference between Algae and Fungi

• Fungi are saprophytes. They depend on dead and decaying organic material for nutrients while algae are autotrophs. 
• Algae are very different from fungi, which have chitinous cell walls and no chlorophyll. Both, however, exist as lichens and have a symbiotic connection.
• Algae (often green algae) receive protection from fungi, and fungi receive nutrition from algae.

The Life Cycle of Algae 

• Haplontic life cycle: The plant is haploid throughout. A diploid zygote is created when gametes (which are created by mitosis) combine. The zygote proceeds through meiosis and produces meiospores, which grow into young algae.
• Diplontic life cycle: The body of the sporophytic plant is diploid. The zygote is created by fusing haploid gametes.
• Diplohaplontic life cycle: In the lifetime, haploid and diploid stages are equally dominant. While diploid sporophytes reproduce asexually, haploid gametophytes proliferate sexually.
• Triphasic life cycle: The life cycle alternates between three generations.

• Gametophyte is the dominant stage in a haplontic system. There are two haploid and one diploid generation in the life cycle. 
• Sporophyte, the dominant stage in a diplobiontic organism, There are two diploid and one haploid generation in the life cycle.

Summary

Algae are autotrophic eukaryotes that have one or more cells that are capable of photosynthetic activity. Algae can also be microscopic multicellular (likely leaf-like Giant kelps or unicellular. Chlorophyll is a pigment found in the majority of algae, which are photoautotrophs. Chlorophyll a and b, as well as carotenes, are the pigments found in chlorophyta. Algae are quite sensitive to the condition of the water. They serve as bioindicators of environmental toxicity.

Frequently Asked Questions 

1. Are there Roots in Algae?
Ans. Algae don’t have actual roots. Algae have hold-fast organs in place of roots, which serve as anchors and keep immobile algae attached to a solid substrate.

2. Describe Kelp Forests.
Ans. Brown multicellular algae make up kelp. They live in shallow waters close to the beach. Several small invertebrates and fish breed in dense, thick-grown kelp. Carnivores such as seals and sea lions eat kelp by diving into it, forming an ecosystem.

3. Are Humans Harmed by Algae?
Ans. Algae pose no threat. Some algae create toxic substances that are dangerous to people. Fever, diarrhoea, and skin rashes are the results of direct exposure to these poisons.

4. Are Algae Capable of Producing Biofuel?
Ans. Following numerous stages, the energy-dense oil produced from algae is transformed into different types of fuel. Each species has a different process.

5. What Occurs if the huge Kelp is Removed?
Ans. Algae with their many cells can regenerate. If the environment is right, the damaged component can regenerate into a new body. If not consumed by herbivores, it otherwise deteriorates and decomposes.

Introduction

The digestive system is made up of organs that digest food, assimilate its nutrients, and eliminate any leftover waste. The gastrointestinal (GI) tract, which connects the mouth to the anus, is essentially a long, continuous tube. For a variety of harmful bacteria, the alimentary canal serves as an immunological barrier. Gut-associated lymphoid tissue (GALT) and the various pH conditions that exist throughout the alimentary canal perform this role.

What is the Alimentary Canal?

Because of their complicated body plans, humans have a digestive tract with two openings: a mouth at one end and an anus at the other. The food material travels in a single path along the alimentary canal as it passes through several specialised organs. The Alimentary Canal is a similar tube whose main purpose is to facilitate food particle circulation and ultimately assist in nourishment.

Check out online study options are a great way to clear the science concepts you need. Study Science class 7th Lesson 2.

Parts of Alimentary Canal 

Mouth: The mouth, also known as the oral cavity or buccal cavity, where the alimentary canal starts, contains teeth and a tongue that help break down food particles.

Pharynx: It is commonly referred to as the throat area. When food is swallowed, it travels via the pharynx.

Oesophagus: The throat and stomach are connected by a lengthy tube called oesophagus.

Stomach: The stomach is a structure that resembles an extended pouch that is situated between the oesophagus and the small intestine. Here, the food is transformed into a liquid suspension to facilitate absorption.

Small Intestine: As a result of the high rate of nutrient absorption in this area, it is sometimes referred to as the “workhouse” of digestion. It is the Alimentary Canal’s longest section.

Large Intestine: The alimentary canal’s terminus is located here. The “leftovers” in this area are used to absorb water and vital nutrients, which are eventually expelled through the anus

The Structure and Parts of Stomach

• The lower surface of the stomach’s curve to the left and the upper surface to the right is referred to as the lesser and larger curvatures, respectively. 
• The fundus, body, and pylorus are its three parts. The fundus, which is the main part of the stomach, is elevated above the esophageal entrance. 
• The stomach’s body and pylorus are it’s middle and base, respectively. 
• The incisura angularis is the point where the body region and the proximal antrum converge.
• The muscularis mucosa, a thin layer of smooth muscle, is composed of the inner mucus epithelium, a bigger loose connective tissue called laminar propria, and the innermost layer of the gastrointestinal wall, known as the mucosa.
• Connective tissue, blood vessels, alveolar tissue, and Meiisner’s nerve plexus make up the submucosal layer.

Which are the Parts of the Alimentary Canal and What are their Functions?

Parts of Alimentary Canal	Structure	Functions
Buccal Cavity	The vestibule and actual oral cavity make up the mouth.  A hard palate is the roof of the mouth, which divides the nasal cavity from the oral cavity. The muscular tongue has numerous taste buds and covers the base of the mouth. Dentin makes up teeth, which are covered in enamel, the toughest tissue.	Ingestion of food. Tongue helps in producing the sense of taste by detecting chemicals present in food. Teeth chew and grind the food material into smaller pieces. During mastication, incisors are used for cutting the food pieces, canines for tearing, premolars and molars for chewing and grinding.
Pharynx	It is a muscular structure resembling a tube.  It connects to the oesophagus and the trachea, two passages.	Here, swallowing is carefully timed to prevent food particles from entering the trachea.
Oesophagus	It is a muscular, extensible, mucus-coated tube that runs from the pharynx to the stomach.  At each end, a muscular sphincter protects it.	Peristalsis causes the bolus to move toward the stomach. The lower or cardiac sphincter stops food from passing from the stomach back into the oesophagus.
Stomach	Just behind the diaphragm is where the stomach is located. Chief cells, which secrete the enzymes found in gastric juice, parietal cells, which secrete hydrochloric acid, and intrinsic factors, which work in conjunction with vitamin B12 to preserve the lining of the stomach wall, cover the inner surface of the stomach and its glands.	Releases hydrochloric acid, which helps to break down food particles, and activates dormant pepsinogen to produce pepsin, which aids in the breakdown of proteins.  Along with food, it also contributes to bacterial death.
Small Intestine	In the abdominal cavity, the small intestine looks like a lengthy, coiling loop.  There is a brief duodenum section, then the jejunum region, and the longest region, the ileum.  The mucosal layer, which is the small intestine’s innermost layer, is covered in numerous microscopic folds known as villi.  The vermiform appendix, a structure that resembles a worm and is located at the back of the small intestine, has no known physiological function.	The small intestine’s surface area is increased by microvilli, which improves food absorption.  In the small intestine, the presence of secretory cells at the base of crypts prevents bacterial development.  The duodenum is where food is continuously broken down, whereas the jejunum and ileum primarily help the body absorb the food that has been digested.
Large Intestine	It resembles a large muscular tube connecting the rectum and small intestine.  It consists of the anus, colon, rectum, and caecum.  There are sigmoid, transverse, ascending, and descending sections in the colon.  The caecum is a structure resembling a pouch.	The lubricating mucus covered in faeces is produced by the existing intestinal mucus glands.  Here, undigested food stuff concentrates and salts and water are absorbed.  The rectum acts as a holding area for faces.

Summary

Because of their complicated body plans, humans have a digestive tract with two openings: a mouth at one end and an anus at the other. The lower surface of the stomach’s curve to the left and the upper surface to the right are referred to as the lesser and larger curvatures, respectively. In the abdominal cavity, the small intestine looks like a lengthy, coiling loop. The lubricating mucus covered in faces is produced by the existing intestinal mucus glands.

Frequently Asked Questions (FAQs)

1. What is the Function of the Epiglottis?
Ans. Epiglottitis is a flap-like structure that covers the glottis, the windpipe’s entrance, when food is swallowed. This stops the food from choking and entering the windpipe.

2. What Function does Meiisner’s Nerve Plexus Serve?
Ans. Meissner’s nerve plexus controls the gastrointestinal tract’s secretions and local blood flow and aids in the start of the peristaltic movement.

3. Where are Delta Cells Found and what do they do?
Ans. The pancreatic islets of Langerhans contain delta cells. Somatostatin, a hormone that prevents the body from producing other hormones, is produced by these cells.

4. What Pigments are Present in Bile, and where do they Come From?
Ans.  The bile pigments include greenish biliverdin and yellowish bilirubin. Dead red blood cells’ haemoglobin is degraded, and the bile pigments that result are expelled.

5. What Function does E. coli Serve in the Human Digestive System?
Ans. E. coli is a type of bacteria that helps with digestion, breaking down food particles for absorption in the small intestine and producing vitamin K.

Introduction

Agriculture has played a significant role in the rise of human civilization, but organic farming of domesticated species has produced food surpluses that have enabled people to live in urban areas. Agriculture is the art and science of creating and cultivating soil, increasing yields, and keeping animals. Agriculture and farming have historically been essential to human life. The expansion of agriculture and farming was a factor in the development of civilization.

What is Agriculture? 

Agriculture is characterized as the practice of growing plants and animals for human consumption. Various parameters need to be considered in agriculture, such as the type of crop, soil characteristics, environment, and so forth. Farmers decide which crop should be cultivated at what time and location based on these parameters. Aside from that, reasonable soil, environment, and season are insufficient to produce a high-quality product. It necessitates several tactics that need to have been used.

Want to get an “A” on your Science exams? Let our expert teachers be your guide toward improving your grades and reaching your highest potential. Watch the related video of this chapter in Class 8th Science lesson no 1.

Importance of Agriculture

Social and Economical Aspect:

• Agriculture increases the availability of food, which improves population nutrition and promotes population health. 
• A small number of people cannot do agriculture. Each of its processes requires the input of numerous persons. Consequently, this results in the creation of jobs.

Environmental Aspect:

• Waste management depends heavily on agriculture. The biodegradable wastes can be transformed into manure, which the plants can use as a source of food.
• With the right treatment, bare soil can be turned into crops, ensuring agriculture’s efficient use of land resources. 
• It significantly contributes to preserving the microclimate of any location and raises the standard of the ecosystem as a whole.

What are the Basic Agricultural Practices?

Those consecutive actions that are taken to guarantee the proper production of crops are referred to as “agricultural practices.” To guarantee a yield of great quality, this must be done. The next section has a quick discussion of the steps.

Steps of Agricultural Practices

• Preparation of soil:
• • It is crucial to prepare the soil to make sure it is rich, well-drained, well-aerated, uniform, and can hold enough moisture. This stage is essential because the soil must survive numerous adverse situations. After all, it is exposed to them. 
  • Typically, the preparation is carried out with the aid of various tools, such as a hoe and a plow.
  • To provide the best aeration, the soil must be dug out and loosened.
  • To spread the dirt equally and avoid lumping, leveling is done after plowing. 
  • Finally, there is a chance that the soil has run out of nutrients, which could be bad for plant growth. Manure and fertilizers are thus applied to restore it.
• Seed selection and sowing

• Choosing the right seeds is crucial to getting a good crop. 
• A quality seed, also known as an HYV or High Yielding Variety seed, guarantees improved plant growth, increased disease resistance, and increased yield. 
• The chosen seeds must be planted in the prepared field after being chosen. 
• Sowing is the distribution and burying of seeds into the soil, whether by hand or with the aid of machines.
  
• Irrigation
• To meet the crops’ water needs, the best possible amount of water is applied to the soil where the crops are growing. 
• A source of water, such as ponds, wells, rivers, etc., is typically supplied by a variety of channels, such as canals or pipelines.
• Crop maintenance
• • Considering that the crops must grow for a long period and are exposed to the elements, they need some maintenance. 
  • In essence, they can be destroyed by the numerous pests, birds, rodents, etc. that are likely to attack them.
  • Unwanted plants known as weeds can encroach on cropland and compete with crops for nutrients, stifling the development of crops. 
  • To protect them, it is therefore imperative to apply weedicides, insecticides, etc. 
  • To stop bird assaults, farmers frequently construct scarecrows.
• Harvesting
• • It is the process of gathering the crop’s valuable components, and it is typically carried out after the crop is fully mature and has reached its ideal development stage. 
  • It can be carried out manually with implements like a sickle or with the aid of machines.
• Storage

• In this last step, the harvested goods are moved to the granaries or storehouses before being distributed to the market. 
• To prevent desiccation, it is essential to dry the items before storing them, especially grains and pulses.
• The items are additionally fumigated to deter rodent and pest infestations.

What are Sustainable Agricultural Practices?

The concept of sustainability is the prevention of resource depletion by the adoption of specific actions that preserve both the health of the natural world and the future of humanity. Some of the measures taken in agriculture are discussed below.

• Making sure that soil is properly used and prepared to prevent erosion.
• Reducing water use through the application of new methods and tools.
• Drop-by-drop watering is done with drip irrigation, which is time-controlled. In the revolutionary practice of hydroponics, nutrients are dissolved in water and fed to plants to provide them with nutrition.
• The use of biodynamic farming methods is recommended.
• Crop rotation proposes that different crop types should grow in a specific region.
• Promoting the expansion of the pests’ natural predators to reduce the need for pesticides, weedicides, and other chemicals.

Summary

Agriculture is characterized as the practice of growing plants and animals for human consumption. Agriculture increases the availability of food, which improves population nutrition and promotes population health. The biodegradable wastes can be transformed into manure, which the plants can use as a source of food. It is crucial to prepare the soil to make sure it is rich, well-drained, well-aerated, uniform, and can hold enough moisture.  Crop rotation proposes that different crop types should grow in a specific region.

Frequently Asked Questions 

1. Define Pesticides?
Ans. Pesticides are a class of chemicals that include insecticides, herbicides, and fungicides that are used to control pests (harmful organisms) in agriculture. Examples include glyphosate, DDT, etc.

2. Why is it no Longer Advisable to use Fertilizers Today?
Ans. Fertilizers are extremely damaging to the environment. Overuse of fertilizers creates contaminants that travel via the water and air. They obliterate the water and soil microorganisms. They contribute to a phenomenon known as “biomagnification.” So it is not recommended to use more fertilizers.

3. Which Crop Diseases are Prevalent?
Ans. Common bacterial diseases include fire blight, necrosis, and Granville withering. Exfoliation, wheat black rust, and other common fungi-caused illnesses are only a few examples.

 4. What is the Indian “Green Revolution”?
Ans. With the use of technology, agricultural systems in India were transformed into modern industrial systems during the Green Revolution of the 1960s. This period included the use of HYV, mechanized farming tools, irrigation systems, fertilizers, and pesticides.

5. Define Genetically Modified Crops?
Ans. Genetically modified crops are those whose genomes have undergone genetic engineering modifications to exhibit desired features like higher nutrient production and pest resistance. For example, BT brinjal.