Blog

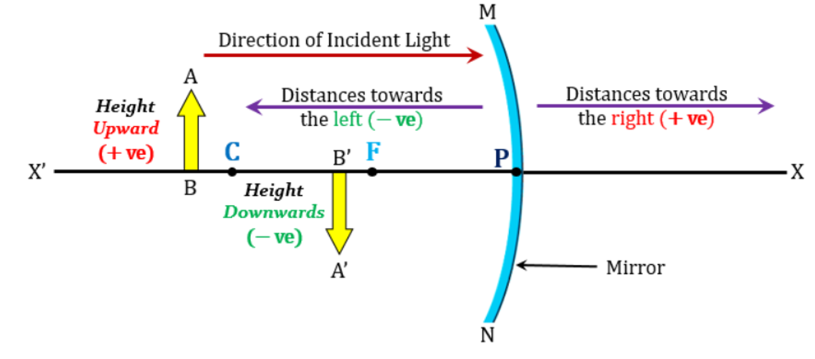
Introduction

The most fundamental application of percentages is to compare two amounts while setting the second amount to 100. The use of percentages is widespread and varied aside from this. For instance, a lot of statistics in the media are expressed as percentages, including bank interest rates, retail discounts, and inflation rates. Percentages are essential for understanding the financial aspects of daily life.

The Latin word “per centum,” which means “per hundred,” is where the word “percent” originates. The task of comparing unlike fractions is very challenging. Because percentages are the numerators of fractions with a denominator of 100. Percentages have a wide range of applications in daily life, including making simple comparisons, allocating discounts in marketing, and calculating profits and losses for businesses.

Percentages

Per means “out of” in percentage, and cent means a century. In essence, the whole is always set to 100, and the relationship is between a part and the entire. The ratio known as a percentage has a denominator of 100 and the percentage symbol %.

The percentage formula is as follows:

How to find percentage from data?

To find percentage from a given data, we first need to find the fraction of the quantity from the given data. By dividing the number by a whole and multiplying the result by 100, any fraction can be expressed in percentages. Consider a society with 1000 members, 650 of whom are voters. Then the percentage of voters out of all the residents is,

% Of voters = × 100

= × 100

= 65%

Percentage of a Number

When a number is divided into 100 equal parts, the percentage of that number is the sum of those 100 parts. Calculating percentages involves multiplying the total number by the percent expressed as a fraction. For instance, let’s say we need to find 30% of 600. We can figure it out as:

30% of 600 = 600 ×  = 180

Here, 600 is total, so 30% of 600 is 180.

Applications of Percentages

One of the most useful mathematical ideas is the percentage, which has applications in practically every branch of science as well as in everyday life.

To compare fractions

Fractions can be converted to percentages to create a clear comparison representation. This is very useful when the denominators of two fractions have different values. For instance, suppose you need to compare the fractions 2/5 and 1/4. We use percentages because making a direct comparison in this situation is very difficult. For 2/5, the percentage form is 40%, and for 1/4, the percentage form is 25%. We can categorically state that 2/5 is greater than 1/4.

To estimate increment or decrement

Any change in a quantity can be expressed in terms of a percentage. For instance, a 20% decrease would occur if a person’s salary was Rs. 5000 per month one year and Rs. 4000 the following.

The formula to calculate % change in a quantity is

Change% = × 100

To calculate ‘How much’ or ‘How many’

Sometimes numbers are expressed as percentages, for example the case of a city where 40% of the people are vegan. Therefore, the percentage will enable us to determine the precise number of vegans.

The formula to calculate the number from percentage is as follows,

Quantity =  × Total

To calculate profit or loss in percentage, to mark discounts etc.

If the selling price and cost price are known, the seller can use percentages to determine its loss or profit. For instance, a seller may charge Rs. 5000 for a fan while only paying Rs. 4000. The profit margin in this case is 25%.

Solved Examples

Example: What is the discount given on an article marked Rs. 6000 with a discount of 30%.

Solution: The discount on the article is given by

Discount% = × 100

Discount = × Marked Price

Substituting values

Discount = × 6000 = Rs. 1800

A discount of Rs. 1800 is given.

Example: By what percentage is Amit’s salary, Rs. 35000, is less than from Sagar’s salary, Rs. 40000?

Solution: The difference between Amit’s and Sagar’s Salaries is

Sagar’s Salary – Amit’s Salary = 40000 – 35000 = Rs. 5000

The percentage difference between their salaries

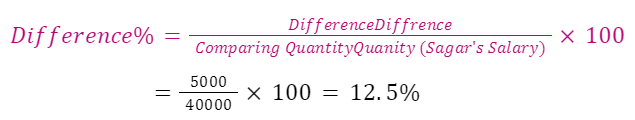
Thus, Amit’s salary is 12.5% less than Sagar’s salary.

Summary

When portions of a quantity are given, we have seen how to convert ratios into percentages. We discussed the formula for calculating the percentage of a number. An increase or decrease in a specified quantity can also be expressed as a percentage. The profit or loss in a specific transaction can be expressed in terms of percentages.

Frequently Asked Questions

1.What is the Importance of Percentage in Sciences other than Mathematics?

Ans. Percentage plays an important role in many aspects of business science, physical science, chemical science etc. In business science (statistics in particular) percentage is used to represent the parts of a data. In physical science percentage is used in various formulae, and derivations to represent efficiency, error and other such things. In chemical science percentage is used to calculate the concentration of different chemicals and composition of solutions etc.

2.How is Percentile Different from Percentage?

Ans. The value in the distribution or level at or below which a specific percentage of the score lies is represented by the percentile. For every hundred, which is the measurement unit, is referred to as the percentage.

3.What is the Relationship between Percentage and Probability?

Ans. Probability of an event can also be expressed as a percentage. For example, if the probability of an event is x, then the percentage probability is given by

% Probability = 𝑥 x 100%

Read More: Ratio and Percentage Formula and Examples

Introduction

Pythagoras, a Greek philosopher who was born around 570 BC, is remembered by the theorem’s name. The theorem has likely been proved the most times of any mathematical theorem using a variety of techniques. The proofs are numerous, some of which go back thousands of years, and include both geometric and algebraic proofs. The Pythagorean theorem is extremely useful when determining the shortest distance between two points or the degree of the mountain slope. In a right-angle triangle the square of the hypotenuse is said to be equal to the sum of the squares of the two legs.

Right Angle Triangle

A triangle with a right angle is one in which one angle is 90 degrees. We refer to this triangle as a right-angle triangle since 90 is also referred to as the right angle. Triangle sides with a right angle were given unique names. The side directly opposite the right angle is known as the hypotenuse. Based on the values of the various sides, the right triangles are divided into isosceles and scalene types.

Properties of Right-Angle Triangle

• The height, base, and hypotenuse of a right-angle triangle are its three sides. 
• The two adjacent sides are referred to as base and height or perpendicular.
• Three similar right triangles are formed if we draw a perpendicular line from the vertex of a right angle to the hypotenuse.
• The radius of a circle whose circumference includes all three vertices is equal to one-half the length of the hypotenuse.
• The triangle is known as an isosceles right-angled triangle, where the adjacent sides to the 90° are equal in length if one of the angles is 90° and the other two angles are each equal to 45°.

Pythagoras Theorem

Pythagoras is a potent theorem that establishes the relationship between the sides of a right-angle triangle. According to Pythagoras’ theorem –

“Square of the hypotenuse is equal to the sum of the square of the other two legs of the right angle triangle”. Mathematically, it may be expressed as

              Hypotenuse² = Perpendicular² + Base² 

Area of the Right-Angle Triangle

The area of the right-angle triangle is the region enclosed within the triangle’s perimeter. The formula for a right-angle triangle’s area is.

Area of right-angle triangle = (Base × Perpendicular)

Facts

• A triangle must be a right triangle if it obeys Pythagoras’ theorem.
• The longest side of a triangle is the one that makes the largest angle.
• When the midpoint of the hypotenuse of a right-angled triangle is joined to the vertex of the right angle, the resulting line segment is half of the hypotenuse. In other words, the center of the hypotenuse is the circumcenter of the right-angled triangle.
• If two sides of a right angle are known, we can find the other side using Pythagoras’ Theorem.
• From the provided value of sides, we may determine whether a right-angle triangle is possible.

Summary

A right-angled triangle is one in which one of the angles is a right angle (90 degrees), and the hypotenuse is the side opposite to the right angle. The hypotenuse square of a right-angled triangle is equal to the sum of the squares of the other two sides, according to Pythagoras’ Theorem.

Solved Examples

Example 1: In the right-angle triangle, If PQ = 5 cm and QR = 12 cm, then what is the value of PR?

Solution:  By Pythagoras theorem, we have, 

   Hypotenuse² = Perpendicular² + Base²

PR² = 5² + 12²

PR² = 25 + 144

PR =  = 13 cm

Hence, the value of PR is 13 cm.

Example 2: If a triangle has three sides 9cm, 5 cm, and 7 am respectively, check whether the triangle is a right triangle or not.

Solution: According to the theorem, if the square of the longest side equals the sum of the squares of the other two sides, a triangle is said to be, a right triangle. 

9² = 5² + 7² 

81 = 25 + 49

81 ≠ 74

 Thus, 81 is not equal to 74. Hence, the given triangle is not a right-angle triangle.

Frequently Asked Questions

1.Which Side of a Right-Angled Triangle is the Longest?

Ans: The hypotenuse of a right-angled triangle is its longest side.

2.What is a Right-Angled Triangle’s Perimeter?

Ans: The perimeter of a triangle is the sum of all sides.

Perimeter = base + perpendicular + hypotenuse.

3.Can there be two Right Angles in a Triangle? Explain.

Ans: No, there can never be two right angles in a triangle. A triangle has exactly three sides and interior angles that add up to 180 degrees. This means that if a triangle contains two right angles, the third angle must be zero degrees, which means that the third side will overlap the opposite side. Therefore, a triangle with two right angles is not possible.

Introduction

An engine used to convert mechanical energy into electrical energy is an AC generator. Steam turbines, gas turbines, water turbines, and other similar devices all generate this energy. It creates a sinusoidal waveform of alternating current. Alternators are another name for AC generators. The electromagnetic induction law of Faraday is the foundation of an AC generator. According to this rule, anytime a conductor is exposed to a variety of magnetic fields, an electromotive force (EMF) is generated across it. This EMF is referred to as an induced EMF. Electromagnetic induction is the term for this phenomenon. Induced electromagnetic induction is the process by which a coil develops a potential difference as a result of changes in the magnetic flux flowing through it. Several types of AC generators, including polyphase generators, rotating field generators and spinning armature generators.

For more details watch the video of the Science Course for classes 6th, 7th, and 8th.

What is an AC Generator?

An AC generator is an engine that converts mechanical energy into electrical energy in the form of an alternating driving force. To provide a consistent magnetic field, an AC generator uses two magnet poles.

AC Generator Parts and Function

An electromagnet with two poles, the North Pole and the South Pole, is a component of an AC generator.  Below is a discussion of certain AC generator components, including the rotor, slip rings, and armature loop.

a. Field

The output voltage of an AC generator is obtained from the source using conductor loops. The field’s main function is to provide a magnetic field that will stimulate the gadget.

b. Armature

The armature coil is a coil that is part of the generator and produces output voltage. An armature coil’s job is to move electricity through the generator.

c. Prime Mover 

The primary mover of an AC generator is either an engine or a turbine. It serves as the appliance’s power supply.

d. Rotor 

A rotor is a revolving component with magnetic field spirals. It generates the necessary output voltage.

e. Stator

A stationary part holding the armature spirals is called a stator. A stator includes three different parts. They are stator frame, stator core, and armature spirals.

1. Stator frame: A frame that grips the stator core and armature spirals.
2. Stator core: There are slots in the inner part of the core that hold the armature spirals. A steel or iron is coated on the walls of the stator core to decrease the eddy current losses.
3. Armature winding: They are bounded on the stator core.

f. Slip Rings

There are two small rectangular blocks fixed with slip rings called carbon brushes. They are attached to the galvanometer.

Principle of Electric Generator

The basis of AC generators is Faraday’s law of electromagnetic induction. A current-carrying coil placed in a consistent field of force produces the driving force that is referred to as the law.

Construction and Working of an AC Generator 

An AC generator consists of a rectangular coil with two magnet poles attached to it on either side. Two rings are used to fasten the coil’s (or loop’s) perimeter. The rings are joined together with brushes. When a conductor travels in a magnetic field, an electric 

The generator induces a current in it.

Between the magnet’s poles, a rotating rectangular coil, also known as an armature, is used. The magnetic field’s vertical axis is the centre of rotation. The flux in contact with the armature changes as it rotates constantly. The alteration in flux results in the generation of an emf. As a result, the galvanometer, slip rings, and carbon brushes produce an electric current. While direct current only travels in one direction, alternating current sometimes flips direction.

The production of the AC generator shown in the above graph is described as

1. Induced EMF is zero when the coil is at point A because it moves equidistantly from the magnetic field’s curve at that point.
2. A gradient of 90o is created between the coil‘s motion and the magnetic field as it moves from point A to point B, and induced EMF is at its highest level during this time.
3. Moving the coil from A to B results in the same motion being equally far from the magnetic field and no generated EMF.
4. The induced EMF is once more at its highest when the coil is moved from C to D since its motion is antiparallel to the magnetic field and its angle is 270o.
5. The coil completes one cycle and moves equally far from the magnetic field when it moves from D to A. Induced EMF is therefore zero.

Advantages of AC Generator Over DC Generator

Category	AC Generator	DC Generator
Output Voltage	Higher Output Voltage.	It cannot generate a higher output voltage as it damages the functioning of the commutator.
Construction	Simpler construction	Construction is complicated due to a commutator.
Functioning	Works on the principle of electromagnetic induction.	DC generator functioning is more complex than an AC generator.
Maintenance	It demands less maintenance.	It demands more maintenance than an AC generator.
Cost	Cheaper	Costs higher than AC generator
Efficiency	Transmission efficiency is higher as AC reduces transmission losses.	Transmission efficiency is lower.

You can also read “What is AC Voltage Capacitor?” for explanation of AC voltage.

Summary

A generator is an engine that changes one type of energy into another. Large currents are produced by electric generators for usage in industrial and domestic applications. There are two different kinds of electric generators: DC generators, which convert mechanical energy into direct current. A generator of alternating current that converts mechanical energy. On the Faraday law of EMI theory, an AC generator was placed. In an AC generator, the flux in contact with the armature varies as it rotates continuously. The shift in flux causes an emf to be generated. As a result, the galvanometer, slip rings, and carbon brushes produce an electric current. As an AC generator produces higher output voltage, it is easier to build, requires less maintenance, is more efficient, and is less expensive than a DC generator. Large currents are produced by electric generators for usage in industrial and domestic applications.

Frequently Asked Questions 

1. Can we Generate EMF without Rotating the Coil in an AC Generator? Explain.

Ans: Yes, emf may be produced without the coil revolving. If the armature is made to move at a velocity perpendicular to the magnetic field, Emf can also be produced.

2. What is the reason for Heat Loss in the Generator?

Ans: Reasons for the heat loss in the generator can be, (a) generation of the by-products like carbon dioxide, and molecular friction, which can reduce the efficiency. The heat loss hinders the efficiency of the generator. So, the efficiency is never 100%. 

3. What is the Driving Force?

Ans: Induced emf is also termed as the driving force and can be expressed as, 

                                                      ε = N B Aωsinωt

where N is the number of turns in the coil, B is a magnetic field, A is an area, ω is the angular velocity

So, in an AC generator, the induced emf is proportional to the applied magnetic field.

4. Give examples of DC Sources.

Ans: The electrical appliances like radios, televisions, and solar panels. DC only travels in one direction and lacks any polarity.

Introduction

In simple words, a reflecting surface is a mirror. The research about mirrors dates back centuries, in Germany, mirrors were first created 200 years ago. Famous chemist Justus Von Liebig discovered mirrors in the year 1835, where the transparent glass was converted into mirrors by applying a coating of silver on one side of it. There are several proofs of using polished metal surfaces as mirrors in ancient civilizations. There are some types of mirrors that can reflect sound, which is an intriguing feature of mirrors, known as acoustic mirrors. In World War 2, those that could hear the sounds made by enemy aircraft were used.

What is Mirror?

A reflecting surface is a mirror. The law of reflection governs how a mirror functions. According to the law of reflection, when a light ray strikes a reflective surface, the incident light ray, the reflected light ray, and the normal all lie in the same plane, and the angle of incidence and angle of reflection are both equal.

Improve your Science concepts. Study Science Subject for classes 6th, 7th, and 8th.

Types of Mirrors

There are three types of mirrors that are widely used

a. Plane Mirrors

A smooth reflecting flat surface characterises plane mirrors. We utilise these common mirrors most frequently in our daily life. The reflection of the image in a plane mirror is in the same proportion as the original, but the images are inverted from left to right.

b. Convex Mirrors

Convex mirrors are spherical mirrors. These mirrors have an outward curvature. Convex mirrors provide a simulated, erect, and reduced image. These also go by the name of diverging mirrors.

c. Concave Mirrors

Concave mirrors are spherical mirrors as well, but they have an inward curve. The positioning of the object affects the concave mirror’s ability to produce an image. These also go by the name of converging mirrors.

Mirror Formula

The relationship between an object’s distance, an image’s distance, and the focal length of the mirror is given by the mirror equation/mirror formula. If the distance between the object and the mirror is u, the distance between the image and mirror is v, and f is the focal length of the mirror. Then the mirror formula can be expressed as

                                                                                                                      1⁄f = 1⁄u + 1⁄v

What is Magnification?

Magnification is an increase in the size of the image that a spherical mirror produces about the size of the item. The height of the picture to the height of the object is known as the magnification ratio.

Magnification Formula for the Mirror?

The magnification formula of the mirror can be given as,

                                                                                                m = h‘⁄ h

Where m is the magnification, h’ is the height of the image, and h is the height of the object.

The Magnification Formula of the Mirror can also be given as,

                                                                                           m = –v ⁄ u

where m is the magnification, v is the distance between the image and mirror, and u is the distance between the object and mirror.

Therefore, if the height of the object and image are equivalent, then the magnification will be equal to 1. Magnification will be greater than 1, or the image will be enlarged, if the image size is larger than the object size. Image size will be reduced if the image is smaller than the object, or if the magnification is less than 1.

Concave mirrors can either generate an erect or inverted picture depending on the object’s location, while convex mirrors always provide an upright image. As a result, depending on where the item is maintained, the magnification of a convex mirror is always positive, whereas the magnification of a concave mirror can be either positive or negative. Convex mirrors usually create pictures with lower quality, therefore their magnification is less than 1.

Summary

Concave, convex, or plane surfaces can all reflect light, including mirrors. The relationship between an object’s distance, an image’s distance, and the focal length of the mirror are known as the “mirror equation” or “mirror formula.” Magnification is an increase in the size of the image that a spherical mirror produces about the size of the item.

Frequently Asked Questions (FAQs)

1.What is the Focal Length of a Mirror?

Ans: Focal length is the distance between the Centre of the mirror and the focus of the mirror. And Focus is the point through which the reflected light rays pass when incident light rays are parallel to the principal axis. The focus is on the midpoint of the pole and centre of curvature. We can find the focal length of any mirror using the below formula

                                                                                                           1⁄f = 1⁄u + 1⁄v

In most cases, the focal length is given in millimeters/centimeters. We may determine the angle of view, how much of the scene will be reflected in the mirror, and the mirror’s magnification by looking at the focal length.

2. What is Normal?

Ans: Normal is a line that is drawn perpendicular to the mirror’s surface. The term “Normal line” refers to this line. The incident angle and reflected angle are split into two equal angles by the normal line. It is a fictitious line. The angle of incidence and angle of reflection are terms used to describe the angle between an incident ray and the normal and the angle between a reflected ray and the normal, respectively. To understand what occurs when the angle of incidence, angle of reflection, and angle of refraction vary, a normal is drawn.

3. What is the relation between Focal Length and Magnification?

Ans: Magnification decreases as focal length increases, and thus the mirror magnification is inversely related to the focal length of the mirror. 

Since, the mirror formula can be expressed as,

                                                                     1⁄f = 1⁄u + 1⁄v

And the formula for the magnification of the mirror is,

                                                                   m = –v ⁄ u

Thus, by combining the above two equations, we can get,

                                                                     m = –f ⁄ f-u

Therefore, mirror magnification decreases with increasing focal length, while mirror magnification increases with decreasing focal length. The relationship between the mirror’s magnification and focal length is shown above.

Introduction

Two lines can intersect at any point or come together at a common point to form an angle. An angle is defined as having two arms that extend outward, and its measurement is expressed in degrees. Angles in pairs are the related angles. Any pair of angles that have a specific relationship between them is therefore referred to as related angles. A specific name refers to these angles. Since the angles are related to a particular circumstance, they are known as related angles.

Related Angles

Related angles are those that have a particular relationship with one another. Each pair of connected angles is given a unique name. There is a specific standard for the associated angles.

Types of Related Angles

The related angles have specific names depending on the type of criteria. When the sum of the two angles is 90 degrees, they are said to be complementary angles. If the sum of the two angles is 180 degrees, they are said to be supplementary angles. In a plane, two angles are said to be adjacent if they share a common vertex, a common arm, and non-common arms that are on the opposite side of the common arm. Due to their shared arm, adjacent angles always lie next to their other pair. The two adjacent angles are regarded as a linear pair of angles when the sum of their respective measures equals 180 degrees. Since their non-common arms are two rays pointing in opposite directions, they are known as linear pairs of angles. When a transverse crosses parallel or non-parallel lines, various angles are created. Alternate exterior angles, alternate interior angles, vertically opposite angles, and corresponding angles are the different types of angles.

Complementary Angles

Complementary angles are those where the sum of the measures of two angles is 90 degrees.

Supplementary Angles

These angles are referred to as supplementary angles when the sum of the measures of two angles is 180 degrees.

Adjacent Angles

If two angles in a plane share a vertex, a common arm, and their non-common arms are located on opposite sides of the common arm, then the angles are said to be adjacent.

Adjacent Angles: Linear Pair

If two adjacent angles share a common vertex, a common arm, and non-common arms that are oriented in opposition to one another, they are referred to as linear pairs of angles.

Alternate Exterior Angles

The angles outside the parallel lines and on the opposing sides of a transversal that intersects parallel lines are referred to as alternate exterior angles. Every other exterior angle is equal.

Alternate Interior Angles

The angles inside the parallel lines and on the opposing sides of a transversal that intersect parallel lines are referred to as alternate interior angles. All of the interior angles alternately are equal.

Vertically Opposite Angles

The angles are formed by two lines’ intersections, which are opposite. The angles that are vertically opposite are always equal in size.

Corresponding Angles

The angels that are lying parallel to the lines and on the same side of the transversal are always equal. Corresponding angles is the name given to these angles.

Interesting Facts about Related Angles

The linear angles’ and supplementary angles’ combined measures are equal. But the specifications for each of these angles vary. The placement of the angles is what causes this. A common arm will always connect the linear pair of angles. The supplementary angles, however, don’t always follow the same pattern. As a result, while all supplementary angles are not linear pairs, all linear pairs are supplementary angles.

Solved Examples

Example: Solve for x in the following images.

Solution: 

1.This is a linear pair that lies on line AB.

∠AOC + ∠COB = 180°

120° + x = 180°

x = 180 – 120

x = 60°

1.This is a pair of vertically opposite angles

x = 90°

1.Here, we have no direct connection between a given angle and the angle measured x.

Thus, we will use corresponding angles to find ∠CPO, to use the relation between ∠CPO and x.

∠CPO = ∠AOE

∠CPO = 130°

Now, ∠CPO and ∠OPD are a linear pair on the line CD.

∠CPO + ∠OPD = 180°

130 + x = 180

x = 180 – 130

x = 50°

Summary

There are specific requirements for the related angles. There are always two of them. The angles are referred to as supplementary angles if the total of the pair of angles is 180 degrees. The complementary angle pairs also add up to 90 degrees. The angles that are next to each other are those that have a common arm and other arms that are on different sides of the common arm. Adjacent angles make up the linear pair of angles. The linear pair of angles add up to 180 degrees.

Frequently Asked Questions (FAQs)

1.What are Related Angles?

Ans. Related angles are a pair of angles that have some sort of relation in their geometric structure, which gives them a relationship mathematically using a simple equation.

2.What is the Relationship between Angles on the Same Side of Transversal?

Ans. Angles on the same side of the transversal are shown below,

These angles are supplementary to each other, i.e., the sum of these two angles is 180 degrees.

In a pair of lines and a transversal, if corresponding angles are equal. What does it say about the pair of lines?

If in a pair of lines and a transversal, if the corresponding angles are equal, the pair of lines are parallel.

3.Are all Supplementary Angles Linear Pairs?

Ans. No, all supplementary angles are not linear pairs, since by definition linear pairs are the adjacent angles whose sum is 180 degrees, but for supplementary angles, the condition of adjacent angles need not be fulfilled.

Introduction

To measure the focal length, the distance of the object or image from the mirror, and the mirror’s magnification when studying the reflection of light by spherical mirrors and the generation of pictures by spherical mirrors, several sign conventions must be learned. A spherical mirror‘s pole, sometimes referred to as the origin or origin point, serves as the source of all signals. This sign convention is known as the New Cartesian Sign Convention.

Sign Convention for Reflection by Spherical Mirrors

The sign convention for the mirror was developed with the notion that items are always placed on the left side of the mirror, causing incident light to pass from left to right. For spherical mirrors, the following sign convention applies:

• From the pole, every measurement is taken.
• When measured in the direction of the incoming light, distances are thought of as positive; but, when measured in the opposite direction, they are thought of as negative.
• Upward values are positive and descending values are negative when measuring distances perpendicular to the main axis.

Sign Convention Diagram

Sign Convention for Concave and Convex Mirror

Concave Mirror Sign Convention

• The distance of the object seems to be negative since it is always in front of the mirror.
• The concave mirror’s focal length and radius of curvature are both viewed as negative since the focus and centre of curvature are in front of the concave mirror.
• The distance is determined as – (negative) when the image forms in front of the mirror and as + (positive) when it does so behind the mirror (positive).
• When an image is upright, height is positive; when it is inverted, height is perceived negatively.

Convex Mirror Sign Convention

• The object distance is displayed as negative since the object is always in front of the mirror.
• The radius of curvature and focal length are viewed as + (positive) in the case of a convex mirror since the centre of curvature and focus is located behind the convex mirror.
• Since convex mirrors always form an image behind a mirror, the image’s distance is considered to be positive.
• Since an upright image always forms when using a convex mirror, the image’s height is seen as positive.

Mirror Formula

The distance between an object’s main axis point and the mirror’s pole is referred to as the object distance and is presented by u. The image distance is the distance between a spherical mirror‘s pole and the location of an item on its primary axis and marked with v. Therefore, the formula for the focal length (f) in a spherical mirror can be expressed as                                                                                                                                                                                                      1⁄f = 1⁄u + 1⁄v

Summary

To understand the relationship between the object distance, its image distance, and focal length, the Sign convention is a crucial component of this topic. Additionally, due to the Cartesian system we utilise in the unique mirror sign convention, all mirrors have distinct signs for many variables. We put up a relationship between them using the mirror formula to gain a clearer image, and we can utilise this relationship to solve our numerical difficulties.

Frequently Asked Questions (FAQs)

1. Is the Object Distance Positive or Negative in the Concave Mirror?

Ans: A concave or convex mirror’s object distance is always negative because objects are always positioned on the left side of the mirror, and a spherical mirror’s sign convention dictates that distances to the left of the mirror are always negative. When an image forms on a concave mirror, the image distance v will be negative if it does so on the left side and positive if it does so on the right.

2. What is a Virtual Image?

Ans: Anything that is placed in front of a mirror produces an image. The image is a real image if the object’s light rays strike the mirror, reflect off of it, and then coalesce to form the image. If the image must be produced by extrapolating the reflected light beams backwards rather than converging, it is referred to as a virtual image. Any kind of mirror, whether concave, convex, or planar, may create a virtual picture. These pictures are displayed on the lens or the mirror.

3. What is the Sign Convention we use in the Concave Mirror?

Ans: The object’s symbol is interpreted negatively since it is constantly placed in front of the mirror. The focal length and radius of curvature have negative signs because the concave mirror‘s centre of curvature and focus are in front of it. An image’s height is seen positively while it is upright and negatively when it is inverted. When an image forms in front of the mirror, the distance is estimated as – (negative), and when it forms behind the mirror, the distance is calculated as + (positive) (positive).

Introduction

The Mughal Dynasty, which controlled India from the 16th to the 18th century, was founded by Babur. It is one of India’s longest-reigning dynasties was the Mughals. Except for a few regions in south India, they controlled most of the Indian subcontinent. One of India’s most powerful dynasties, the Mughals were the first to rule the nation on their own. Before the Mughals, all earlier dynasties originated outside of India and maintained their cultural allegiance to their nations. They governed for 200 years and seven generations, claiming India as their nation. 

The Mughal emperors who governed India are as follows-

Babur

Babur (1526-30)

• Babur was the son of Umar Sheikh Mirza, the former ruler of Fergana, which is situated to the north of the Hindukush Mountain. He was only 12 years old when he ascended to power.
• Babur‘s Timurid lineage has led him to look toward India constantly. Punjab was important to him because Taimur formerly ruled there.
• He advanced deeper into northwest India, conquering Sialkot and Lahore.
• Babur was waiting for the ideal time to conquer the interior of India. To assault Ibrahim Lodi, he received an invitation from Dauat khan Lodi.
• Babur defeated Ibrahim Lodi in the pivotal battle of Panipat (1526) and took control of Delhi, and Agra.
• Babur imported gunpowder to India, which led to a new style of warfare.
• He defeated Afghans in Ghagara, Rajputs of Chanderi (1528), Rana Sanga at the Battle of Khandwa (1527), and Ibrahim Lodi in the Battle of Panipat (1526). (1529).
• Babur laid the foundation of the Mughal Empire in India.

For more help, you can Refer to Lesson 4 –The Mughal Empire in Social Studies Class 7. Checkout the video Lesson for a better understanding.

Humayun

Humayun (1530-40 & 1555-56)

• Humayun is the son of Babur, and he gained control post the demise of King Babur.
• He initially had a tough time due to the abrupt death of Babur. 
• Also, the elderly Afghans were regaining their footing, and an Afghan soldier named Sher Shah Suri became the Mughal empire’s main enemy. Humayun had to deal with many challenges.
• During the battles of Chausa (1539) and Kannauj (1540), Humayun was defeated and hence, he had to depart for Iran after leaving Delhi.
• He gradually took over Lahore and Delhi after Sher Shah’s demise.
• He passed away in 1556.

Akbar

Akbar (1556-1605)

• Akbar was the son of King Humayun and under the leadership of Bairam Khan, Akbar ascended to the throne following the death of Humayun.
• He defeated Hemu at the Second Battle of Panipat in 1556 with the aid of Bairam Khan, regaining control of Delhi.
• In India, Akbar is regarded as the most significant and influential Mughal emperor.
• He implemented a policy of religious tolerance and used marriage as a diplomatic tool to solidify his connection with the Rajput kings. A Hindu princess was his bride.
• During Akbar’s reign, the Mughal empire grew rapidly. From 1556 to 1605, he ruled over the whole Indian subcontinent.
• Jizyah was dismissed, and Hindu rajas were assigned to positions of authority in his court.
• He founded an Order called Din-e-Ilahi that was based on the Muslim Sufi brotherhood and was open to everyone.

Jahangir

Jahangir (1605-27)

• Jahangir was King Akbar’s son who ascended to the throne in 1605, post the death of King Akbar.
• Because he was the son of a Rajput princess, he followed the policy of fostering stronger ties with Hindu emperors.
• His biggest accomplishment was seizing control of Mewar, which Akbar had previously been unable to do.
• The ruler of Mewar was Rana Amar Singh, and despite Jahangir’s three repeated assaults, he was unable to overthrow Rana.
• When a cease-fire was finally reached, Karan Singh, the son of Rana Amar Singh, visited Jahangir and was warmly welcomed by the emperor.
• He recovered his Mewar domains and made Karan sing a Mansabdar of 5000 ranks.
• In 1627, he passed away.

Shah Jahan

Shah Jahan (1627-58)

• Shah Jahan was the son of King Jehangir and in 1627, he was crowned emperor.
• He began expanding the Mughal sphere of influence in the south. He took control of Bijapur and Golkonda.
• Shah Jhan had a passion for architecture and constructed the Taj Mahal, Moti Masjid, Jami Masjid, and the Red Fort in Delhi.
• Paintings and literary works flourished during his era. In his court, he keeps a magnificent collection of jewels.
• He controlled the Mughal empire until his son Aurangzeb rose in rebellion and imprisoned him for the rest of his life in 1658.
• In jail, he passed away.

Aurangzeb

Aurangzeb (1658-1707)

• He was one of Shah Jahan’s four sons. He imprisoned his father, the emperor, and had all of his brothers murdered. Furthermore, he ruled for a very long time (1658-1707).
• In 1663, he put an end to the Ahom uprising, which broke out again in 1680.
• He laid down severe policies, that were implemented against Sikhs and Hindus.
• Aurangzeb faced opposition from Shivaji and the Marathas.
• He murdered Guru Tegh Bahadur Singh in front of a throng as part of his extremely harsh attitude toward Sikhs.
• He was an orthodox king who once more began the Jizya and imposed high levies.
• After his death in 1707, the Mughal empire collapsed under the weight of his policies, which had brought his enemies together.

Mughal Tradition of Succession

• Compared to other dynasties, the Mughal tradition of succession was particularly unique.
• Primogeniture, the custom of selecting the firstborn son to succeed the parents as monarch, was not practised by the Mughals.
• The Mughals adhered to Timurid norms, which mention each son’s equal claim to the throne. Coparcenary inheritance is the term used.
• The Mughal dynasty’s violent power struggles were because of the equal claim of each son to the same throne. A new revolt sprang out whenever the emperor appeared frail or passed away, and princes began battling with one another for the throne.
• There were several plots and brutal fights during the Mughal succession.
• The emperor used to assign his sons the roles of governors and split his territories among them. The princes had duties to curb the rebellion and protect the empire.
• However, as the princes grew more powerful, they frequently revolted against the monarch and occasionally engaged in conflict among themselves.

Summary

India was made into a vast empire by the Mughals, and during their rule, there were numerous administrative and cultural changes. Hindu rajas were permitted to work in the Mughals’ intricate bureaucracy. The Mughals made their contemporary Rajput rajas into high officers known as Mansabdar and for the first time established a good relationship with them. Mansabdars were aristocrats with the authority to levy taxes.

Frequently Asked Questions:

1.Who was Todar Mal?
Ans: Todar Mal was the revenue officer in Akbar’s court and was highly regarded by the emperor. He was a truthful person.

2.What does the term Sulh-i-Kul mean?
Ans: The word, which means “global peace,” is Persian. This was begun by Akbar; it forbade discrimination based on religion. In Akbar’s view, justice applied to all people.

3.What modifications to the nature of warfare did Babur make?
Ans: Babur introduced gunpowder to India.

Introduction

Babur founded the Mughal empire in 1526 after defeating Ibrahim Lodi in the First Battle of Panipat. In order to establish the empire, Babur had to command a number of military campaigns. Expeditions of Babur include-

• The Battles of Khanwa (1527)
• The Battles of Chanderi(1528)
• The Battles of  Ghagra (1529).

It took almost two decades for Akbar, who rose to the Mughal throne in 1556, to establish his authority and bring central and northern India under his control. His reign saw some significant military campaigns, such as the Second Battle of Panipat in 1556 and the Battle of Haldighati. A number of military conquests were led by Akbar’s successors, Jahangir, Shahjahan, and Aurangzeb, to further the empire’s reach in Mewar, Deccan, Kangra, and Bengal.

Mughal Military Campaign

Gunpowder tactics, in which the Mughals employed cannons to beat their enemies, and well-trained cavalry were the reasons behind the military campaigns’ success. We shall examine in depth the three occasions when the Mughal military campaigns refused to carry on campaigns due to the fear of seasons in those regions.

• A campaign headed by prince Murad Bakhsh in Balkh
• Mughal’s Military campaign in Kashmir
• Mughal Conquest of Assam

A Campaign Headed by Prince Murad Bakhsh in Balkh

• The Mughal emperor Shahjahan led a military expedition in the seventeenth century under the command of his younger son prince Murad Bakhsh to conquer the Uzbek city of Balkh (modern-day Afghanistan). 
• This territory belonged to the Mughals and was taken by Uzbeks under Babur. Balkh’s monarch fled as soon as the Mughal army arrived, and Murad quickly took control of the region.
• Murad eventually made the decision to leave the area. So, he asked for permission to move away from that location.
• Winter was about to arrive in Central Asia at the time, and it was difficult to survive with a sizable force. This was the reason for the request for relocation.
• It was very challenging for them because of the surrounding snow, which could close roads for months and complicate logistics by making it difficult to feed both the sizable army and the horses used for the cavalry.
• Shahjahan rejected his son’s petition and instructed him to stay in position. Murad still left his subordinates there and began his return trip.
• As a result of this, Shahjahan expelled Murad from his court and his mansab was called.

Mughal’s Military Campaign in Kashmir

In 1586, the Chak dynasty of Kashmir was overthrown by the Mughal emperor Akbar.A military expedition to conquer Kashmir was planned under the leadership of Muhammed Qasim Khan. Because of the harsh winter, Mughal troops gradually began to refuse to advance during the capture of Kashmir, forcing Qasim Khan to go out and fight with the enemies on his own. The Mughal soldiers in Kashmir struggled to survive the bitter weather, rough terrain, and unbearable conditions with little to no food supplies.

The Mughal warriors were used to a hotter, more open environment, hence this campaign was difficult for them.

Mughal Conquest of Assam

• The Mughal marched in Assam and Aurangzeb dispatched an army in 1662 with Mir Jumla as its supreme commander.
• The Mughals 1663 sent an army to Assam. The Mughal army successfully conquered the region and compelled the Ahoms to seek sanctuary in the highlands.
• At the conclusion of this campaign, Aurangzeb sent an order to Assam from the Mughal court to select two officials to serve as subedar and faujdar. But, due to the difficulties of the climate they had to endure during the conquest, such as rain and floods, the commanders declined to take the position.
• Ahom took advantage of the circumstance and left their hiding place to begin attacking the Mughal invaders after seeing the helplessness of the Mughal forces.
• In addition, the warriors’ line of communication with one another and the supply of food grains were disrupted by the constant, heavy rain.
• The imperial army fled from Assam as a result of all of these.

Summary

The Mughal military campaigns began in the latter part of the fourteenth century and lasted virtually until the seventeenth. Even though the Mughals were successful in almost all of their conquests, they occasionally faced difficulties in the form of internal insurrection and persistent external pressure. Additionally, environmental considerations presented challenges for the Mughal army. As a result, campaigns like those in Kashmir and Balkh by Murad occasionally had to be abandoned due to unfavourable circumstances. Although many difficulties were faced by the Mughals, their reign is still considered the most powerful in the history of India.

Frequently Asked Questions

1.Who were the Ahoms?
Ans: The tribal communities that moved to Assam were known as Ahoms. They conquered Assam’s traditional landowner elite, known as bhuiyans. The Chhutiyas and Koch-Hajo were also captured by them in the sixteenth century. In the end, they conquered a number of local tribes and established a new, sizable state in the Brahmaputra valley.

2.When and between whom was the Haldighati Fight Fought? Who Emerged Victorious from the Conflict?
Ans: In 1576 CE, Rana Pratap and Akbar’s Rajput armies engaged in combat at Haldighati. Rana Pratap was defeated by the Mughal army under Raja Man Singh’s leadership.

3.Who was Faujdar in the Mughal Era?
Ans: The head of a garrison in the military was known as the “Faujdar” during the Mughal dynasty. These faujdars were later elevated to the position of district chiefs, or sarkars, during Akbar’s rule.

Introduction

Numerous developments occurred at the turn of the 19th century. The world witnessed the effects of modern ideas after the French Revolution, and a wave of modern thought swept the globe. Science witnessed a number of inventions and an influx of contemporary ideas. Two of these cutting-edge concepts rose to the top. A liberal and a radical were ones and the same. These concepts were the result of the industrial revolution’s mechanisation of manufacturing. The liberal philosophy supported the development of property through increasing output.

Industrial Society and Social Change

With the development of the steam engine, the manufacturing process underwent a dramatic transformation, sparking the industrial revolution. The ancient feudal societies were transformed into industrial societies at the height of the industrial revolution in the early 19th century. England was the first European nation to transition into an industrial civilization, and it was here that the first industries were established.

It was a period of building new industries, new cities, and enlarged railroads. It caused a movement from the countryside to the metropolis in pursuit of factory labour, bringing both men and women to the workplace. The unemployment rate rose as the number of workers rose. Long working hours and low pay made it difficult to improve living circumstances. Cities’ housing and sewage issues worsened, and slums began to develop. Instead, because they could now turn their labour into wealth, the workers saw the industrial revolution as a chance to improve their social status.

Coming of Socialism in Europe

The social dynamic shifted as industrial societies emerged in Europe. Villagers abandoned farmland and moved to cities in quest of employment. By the middle of the nineteenth century, socialism had spread throughout Europe. Even though they were creating jobs for people and amassing property for their own use rather than for the benefit of others, socialists were opposed to private ownership. 

Socialists supported local government control over the land. Varied socialists held different opinions; some believed that socialism could be attained by individual effort. The earliest socialists aimed to establish collective production and create a cooperative society; thinkers like Robert Owen and William Morris were among them. Others thought that creating cooperatives fell under the purview of the government.

Following the arrival of Karl Marx, socialism underwent significant growth. He was a German sociologist who immigrated to Britain and rose to prominence as a socialist. He asserted that large manufacturers and private property owners control the current industrial society. He referred to that class as the “capitalist” class and asserted that these powerful capitalists exploit their employees. He referred to contemporary industrial civilization as a capitalist one. It was communism that Marx ultimately wanted to see in society. Marx urged the working class to seize control of the state until communism was achieved because of this.

What is Socialism?

The idea of socialism gained popularity in the 19th century, although its roots may be seen in the writings of classical philosophers like Plato, who discussed a communal society in his work “Republic.” A theory that favours collective ownership above private ownership is known as socialism. In socialism, the society as a whole has authority over the property for the benefit of all of its members. It is not individualistic; instead, it views the community as a whole and emphasises communal goods.

The idea of socialism as an ideology was never fully explored by earlier thinkers like Saint Simon and Robert Owen, who instead focused on collective community. It wasn’t until Karl Marx and his work the critique of political economy that socialism emerged as the dominant ideology.

Marx’s central thesis is that there will inevitably be a class war between the capitalist class and the working class, which will lead to a revolution. One significant way that socialism differs from capitalism is that it emphasises economic equality together with social and political equality.

Spread of Socialism

Marx was crucial in making socialism more widely accepted. In 1864, he created the First International or International Working Men’s Association. It was a group of labour leaders who weren’t fully dedicated to socialism or revolution. This demonstrates Marx’s determination to spread the concept of socialism. The socialist movement had spread throughout Europe by the 1870s. The First International was continued as the Second International on July 14, 1889, due to its success. It was an alliance of socialist and labour parties that carried on the first international mission.

Workers began forming worker unions and cooperatives throughout Europe, particularly in nations like England, Germany, France, and Italy. They formed groups and began organising to fight for their rights, better living and working circumstances, and pay that was fair. The labour union and other labour organisations in England were combined to become the labour party in 1905. The social democratic party took power in Germany. In 1905, the French Socialist Party was also established. The goal of all the numerous types of socialism that emerged over time was to put an end to the class struggle.

Summary

The philosophy of socialism first appeared in Europe in the 19th century. It was brought on by the negative consequences and declining living conditions of industrial workers. According to socialism, a state is a tool for the exploitation of the working class. The concept of class conflict is central to socialism. It asserts that the stronger class has always been taken advantage of by the dominant class. The worker class is taken advantage of by capitalists in today’s capitalist society.

FAQs

1.What is the difference between Socialism and Capitalism?
Ans. According to capitalism, a person is free to amass as much wealth as he likes, and it would be under his control. Capitalism gives primacy to the right to property. Socialism rejects the idea of concentrating wealth in the hands of a small number of people and is opposed to private ownership. Socialism gives the group a higher priority than the individual.

2.What type of Government did the Socialists Support?
Ans. To socialists, the government should assist in the creation of cooperatives and fight to improve a lot of the working class, according to socialists. Socialists favour public management of the available resources.

3.Explain Fabian Socialism.
Ans. This particular brand of socialism emerged in Britain. Instead of discussing the revolution to bring about socialism, it focuses on political parties and seeks to gain power through their sway.

Introduction

The pivotal event that fundamentally altered the nature of politics on a worldwide scale was the Russian Revolution. The Bolsheviks, a Marxist revolutionary group, destroyed the Tsarist government in Russia while the world watched in horror. Early in 1917, the Revolution began, and it lasted until 1923. Two revolutions and the start of a civil war in Russia were part of this insurgent period. It developed over time as a result of the Tsar’s monarchical government’s inefficiency and dishonest practices, growing dissatisfaction among racial minorities, peasants, the military, and workers, Russia’s involvement in World War I, and the dire state of the Russian economy. All of these issues ultimately resulted in a violent Revolution.

Economic and Social Conditions

Before the Russian Revolution of 1917, society was split into royalty and aristocracy, which made up only 12.5% of the population, and peasants, who made up about 82% of the population and the working class, which made up 4%. Russia was unable to participate in the huge Industrial Revolution that other regions of Europe saw. Thus, the middle-class population in Russia did not increase significantly. Only 1.5% of the population was represented. 

Due to the lack of middle-class people, a small number of people have come to control much of the money and power. As a result, the powerful population was ruled by autocratic kings. The majority of the landowners were members of the nobility and royalty. Therefore, those who suffered the most during the Tsarist dictatorship were the rural peasantry and the urban working class. Early 19th-century Russia had extremely low social conditions, from the life expectancy rate to literacy, schools, roads, hygiene, and sanitation.

Russia began to experience industrialization in the early 20th century. It resulted in a number of political and social reforms. Still, agricultural labour was more important in Russia. The peasants who farmed the land were released from serfdom in 1861 by the earlier Tsar Alexander II, but they were never given the opportunity to become proprietors. They laboured in the fields of other landowners since they lacked land. As the government paid the landowners, peasants were given land to work on. The peasants were consequently compelled to reimburse the government for this money. Their discontent was unrestrained. Due to the fact that the majority of lands were privately owned, the peasants attempted to protest this injustice and called for land reform at the beginning of the 20th century. Poor, disgruntled peasants began to migrate to cities almost as soon as the 19th century ended. They were exposed to cosmopolitan ideology and industrialised urban culture.

Policy of Russification

The “Russification” strategy of the Tsar forced numerous nationalities to renounce their culture and languages, which infuriated them. Even Russians had a limited range of privileges. They were supposed to carry out all their responsibilities and demonstrate their unwavering commitment to the rulers. As a result, Tsar Nicholas II’s rule was becoming less and less popular with the populace, which had earlier supported him with slogans like “One Tsar. One Church. One Russia.”

The First World War

In 1914, the First World War added fuel to the already-burning inferno. Russia’s decision to join the conflict increased the need for industry workers to generate war materials. The already irate employees grew enraged. People in general were backing the workers because they shared their opposition to Russia’s involvement in the conflict. The unskilled peasants enrolled as factory workers, while the workers were forced to serve in the military. Millions of Russian soldiers died in World War I before the end of 1916. Russia experienced a severe famine that affected the entire nation. Because of the paucity of military supplies and equipment, which made their defeats worse, the military also began to revolt.

Implications

The military was ordered by the administration to shoot the demonstrators, but they refused. The Russian army’s uprising in February 1917 in and around Petrograd served as the catalyst for the revolution. The troops believed that if the Tsar resigned, Russia’s situation would improve. As a result, the Tsar relinquished his position of authority, and the Russian Provisional Government, which served capitalist interests, took over. The outcomes did not satisfy the working-class folks. Later, the working class joined forces with the extreme-left Bolsheviks to start the infamous October Revolution, which was followed by the Russian Civil Wars, which ultimately resulted in the foundation of the Soviet Union.

Summary

The Russian Revolution was a noteworthy occurrence that forever changed the course of human history. Beginning with the February Revolution, it underwent a number of changes that eventually resulted in the October Revolution, the Russian Civil War, and the transfer of power to the Bolshevik party, which created the Soviet Union. Before the revolution, Russian society was in a precarious state. The Tsarist regime’s careless, dishonest, and inadequate governance, Russia’s involvement in World War I despite its economic ruin, the growing discontent of the peasants, workers, militaries, and ethnic minorities, and differences in political opinions among various groups all contributed to the legendary Russian Revolution of 1917.

Frequently Asked Questions 

1.Before the 1917 Revolution in Russia how was the Situation of Socialist Parties?
Ans. Prior to 1914, the Russian government outlawed all political parties, although in the late 19th century, the Socialists were still actively operating in Russia’s rural districts. The socialists founded the Russian Social Democratic Workers Party in 1898. It adhered to Marxist principles. In 1900, the Socialist Revolutionary Party was also founded.

2.What is Duma and why was it Built?
Ans. Following the people’s strike, the Tsar published the “October Manifesto,” in which he proposed creating a democratic, elective parliament that would give the people more control. The name of this democratic legislature was Duma. However, the Tsar disbanded the first two Dumas because he believed they were not working with him.

3.How did the Revolutionary Tribunal Operate?
Ans. The Revolutionary Tribunals were established during the Russian Revolution and Civil War in order to combat the counter-revolutionaries. It was attempting to stop the elements who wished to destroy the revolution while also advancing it unhindered. When the Provisional Government of Russia was unable to administer justice for the Russian people, it operated as a supporting institution.

4.What Function did the Church Services during the Russian Revolution?
Ans. The Russian Orthodox Church collaborated with the Tsar. By claiming that the Tsar was chosen by God in their official theology, they strengthened the dictatorial rule of the Tsar. They claimed that any demonstrations against their “little father” would be viewed as an insult. Churches received funding for advancing the Tsar’s agenda.