Blog

काव्य को सुनने या पढ़ने में उसमें वर्णित वस्तु या विषय का शब्द चित्र में बनता है। इससे मन को अलौकिक आनंद प्राप्त होता है। इस आनंद और इसकी अनुभूति को शब्दों में व्यक्त नहीं किया जा सकता, केवल अनुभव किया जा सकता है, यही काव्य में रस कहलाता है। 

किसी विनोदपूर्ण कविता को सुनकर हँसी से वातावरण गूँज उठता है। किसी करुण कथा या कविता को सुनकर ह्रदय में दया का स्त्रोत उमड़ पड़ता है, यह रस की अनुभूति है। 

रस के मुख्यतः चार अंग या अवयव होते हैं

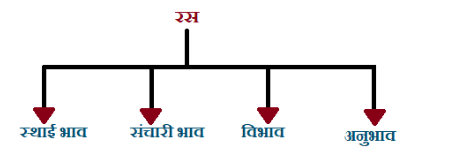
1. स्थायीभाव
2. विभाव
3. अनुभाव
4. व्यभिचारी अथवा संचारी भाव

1. स्थायी भाव

स्थायी भाव का अभिप्राय है- प्रधान भाव। रस की अवस्था तक पहुँचने वाले भाव को प्रधान भाव कहते हैं। स्थायी भाव काव्य या नाटक में शुरुआत से अंत तक होता है। स्थायी भावों की संख्या नौ स्वीकार की गई है। स्थायी भाव ही रस का आधार है। एक रस के मूल में एक स्थायीभाव रहता है।

रसों की संख्या भी ‘नौ’ है, जिन्हें ‘नवरस’ कहा जाता है। मूलतः नौ रस ही माने जाते है। बाद के आचार्यों ने दो और भावों (वात्सल्य व भगवद् विषयक रति) को स्थायी भाव की मान्यता प्रदान की। इस प्रकार स्थायी भावों की संख्या ग्यारह तक पहुँच जाती है और जिससे रसों की संख्या भी ग्यारह है।

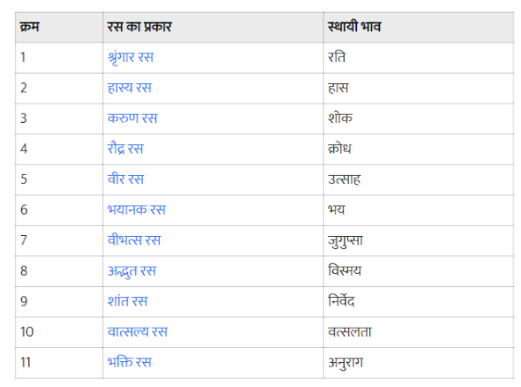
रस और उनके स्थायी भाव

   रस                 स्थायी भाव

1.श्रंगार               रति

2.हास्य              हास्य

3.करुण            शौक

4.रौद्र                क्रोध

5.अद्भुत          विस्मय 

6.वात्सल्य         स्नेह 

7.वीभत्स           घृणा 

8.शांत              निर्वेद

9.वीर             उत्साह

10.भक्ति रस    अनुराग

2. विभाव

जिस वस्तु या व्यक्ति के प्रति वह भाव प्रकट होता है उसे विभाव कहते है।

विभाव दो प्रकार का होता है:

1. आलम्बन विभाव– जिसके कारण प्रति हृदय में स्थायी भाव उत्पन्न होता है, उसे आलम्बन विभाव कहते हैं।
2. उद्दीपन विभाव– भावों को उद्दीप्त करने वाले कार्यों या वस्तुओं को उद्दीपन कहते है। ये आलम्बन विभाव के सहायक एवं अनुवर्ती होते हैं। उद्दीपन के अन्तर्गत आलम्बन की चेष्टाएँ एवं बाह्य वातावरण- दो तत्त्व आते हैं, जो स्थायी भाव को और अधिक उद्दीप्त, प्रबुद्ध एवं उत्तेजित कर देते हैं। 

3. अनुभाव

आलम्बन की चेष्टाएँ (कोशिश करने के लिए, इच्छा) उद्दीपन के अन्तर्गत मानी गई हैं, जबकि आश्रय की चेष्टाएँ अनुभाव के अन्तर्गत आती हैं।

4. संचारी भाव अथवा व्यभिचारी भाव 

स्थायी भाव को पुष्ट करने वाले संचारी भाव कहलाते हैं। ये सभी रसों में होते हैं, इन्हें व्यभिचारी भाव भी कहा जाता है। इनकी संख्या 33 मानी गयी है।

रसों के प्रकार (Ras ke Prakar)

1. श्रृंगार-रस
2. हास्य रस
3. करुण रस 
4. वीर रस
5. भयानक रस
6. रौद्र रस
7. वीभत्स रस
8. अद्भुत रस
9. शांत रस
10. वात्सल्य रस
11. भक्ति रस

(1) श्रृंगार-रस(shringar ras)

श्रृंगार रस को रसराज की उपाधि प्रदान की गई है। 

इसमें नायक नायिका के मिलन और विरह वेदना की स्थिति होती है।

इसके प्रमुखत: दो भेद बताए गए हैं:

(i) संयोग श्रृंगार – जब नायक-नायिका के मिलन की स्थिति की व्याख्या होती है, वहाँ संयोग श्रृंगार रस होता है।

(ii) वियोग श्रृंगार (विप्रलम्भ श्रृंगार) – जहाँ नायक-नायिका के विरह-वियोग, वेदना की मनोदशा की व्याख्या हो, वहाँ वियोग श्रृंगार रस होता है। 

(2) हास्य रस (hasya ras)

किसी व्यक्ति की अनोखी विचित्र वेशभूषा, रूप, हाव-भाव को देखकर अथवा सुनकर जो हास्यभाव जाग्रत होता है, वही हास्य रस कहलाता है। 

बरतस लालच लाल की मुरली धरी लुकाय

सौंह करै भौंहन हंसै दैन कहै नटिं जाय।।

यहाँ पर कृष्ण की मुरली को छुपाने और उसे माँगने पर हंसने और मना करने से हास्य रस उत्पन्न हो रहा है।

(3) करुण रस (Karun Ras)

प्रिय वस्तु या व्यक्ति के समाप्त अथवा नाश कर देने वाला भाव होने पर हृदय में उत्पन्न शोक स्थायी भाव करुण रस के रूप में व्यक्त होता है। 

अभी तो मुकुट बँधा था माथ, 

हुए कल ही हल्दी के हाथ।

खुले भी न थे लाज के बोल,

खिले थे चुम्बन शून्य कपोल। 

हाय! रुक गया यहीं संसार,

बना सिन्दूर अनल अंगार ।

यहाँ पर एक सुहागन के बारे में बताते हुए कह रहे है की अभी तो उसके हाथों में हल्दी लगी थी और बोलने में भी शर्म थी। उसके माथे का सिंदूर इसके पति के मरने के कारण लाल आंगर बन गया है। 

इसलिए यहाँ पर करुण रस है।

(4) वीर रस(veer ras ki paribhasha)

युद्ध अथवा शौर्य पराक्रम वाले कार्यों में हृदय में जो उत्साह उत्पन्न होता है, उस रस को उत्साह रस कहते है। 

हे सारथे ! हैं द्रोण क्या, देवेन्द्र भी आकर अड़े, 

है खेल क्षत्रिय बालकों का व्यूह भेदन कर लड़े।

मैं सत्य कहता हूँ सखे! सुकुमार मत जानो मुझे,

यमराज से भी युद्ध में प्रस्तुत सदा जानो मुझे।

यहाँ पर श्री कृष्ण के अर्जुन से कहे गए शब्द वीर रस का कार्य कर रहे है।

वीररस के चार भेद बताए गए है:

1. युद्ध वीर
2. दान वीर
3. धर्म वीर
4. दया वीर।

(5) भयानक रस(Bhayanak Ras ki Paribhasha )

जब हमें भयावह वस्तु, दृश्य, जीव या व्यक्ति को देखने, सुनने या उसके स्मरण होने से भय नामक भाव प्रकट होता है तो उसे भयानक रस कहा जाता है। 

नभ ते झपटत बाज लखि, भूल्यो सकल प्रपंच। 

कंपित तन व्याकुल नयन, लावक हिल्यौ न रंच ॥

इस वाक्य में वातावरण के अचानक बदलने और शरीर में कम्पन और आंखों में व्याकुलता के द्वारा भयानक रस दिखाया गया है।

(6) रौद्र रस(Raudra Ras)

जिस स्थान पर अपने आचार्य की निन्दा, देश भक्ति का अपमान होता है, वहाँ पर शत्रु से प्रतिशोध की भावना ‘क्रोध’ स्थायी भाव के साथ उत्पन्न होकर रौद्र रस के रूप में व्यक्त होता है। 

श्रीकृष्ण के सुन वचन अर्जुन क्रोध से जलने लगे । 

सब शोक अपना भूलकर करतल-युगल मलने लगे ॥

संसार देखे अब हमारे शत्रु रण में मृत पड़े। 

करते हुए घोषणा वे हो गये उठकर खड़े ॥ 

उस काल मारे क्रोध के तन काँपने उनका लगा। 

मानो हवा के जोर से सोता हुआ सागर जगा ॥ 

मुख बाल-रवि सम लाल होकर ज्वाल-सा बोधित हुआ।

प्रलयार्थ उनके मिस वहाँ क्या काल ही क्रोधित हुआ ॥

यहाँ पर श्री कृष्ण की निंदा और अपमान सुनकर कृष्ण में रौद्र रस्बकी उत्पत्ति होती है।

(7) वीभत्स रस (Vibhats Ras)

घृणित दृश्य को देखने-सुनने से मन में उठा नफरत का भाव विभाव-अनुभाव से तृप्त होकर वीभत्स रस की व्यञ्जना करता है।

रक्त-मांस के सड़े पंक से उमड़ रही है,

महाघोर दुर्गन्ध, रुद्ध हो उठती श्वासा। 

तैर रहे गल अस्थि-खण्डशत, रुण्डमुण्डहत,

कुत्सित कृमि संकुल कर्दम में महानाश के॥ 

यहाँ पर माँस, दुर्गन्ध आदि के कारण उठी नफरत के भाव को वीभत्स रस कहा गया है।

(8) अद्भुत रस (Adbhut ras ki paribhasha)

जब हमें कोई अद्भुत वस्तु, व्यक्ति अथवा कार्य को देखकर आश्चर्य होता है, तब उस रस को अद्भुत रस कहा जाता है। 

एक अचम्भा देख्यौ रे भाई। ठाढ़ा सिंह चरावै गाई ॥

जल की मछली तरुबर ब्याई। पकड़ि बिलाई मुरगै खाई।। 

यहाँ पर मछली के अद्भुत कार्य की उसे बिल्ली ने पकड़ा और मुर्गे ने खाया के कारण अद्भुत रस उत्पन्न हो रहा है।

(9) शान्त रस(shant ras )

वैराग्य भावना के उत्पन्न होने अथवा संसार से असंतोष होने पर शान्त रस की क्रिया उत्पन्न होती है। 

बुद्ध का संसार-त्याग-

क्या भाग रहा हूँ भार देख? 

तू मेरी ओर निहार देख-

मैं त्याग चला निस्सार देख। 

यहाँ पर बुद्ध के संसार त्यागने से उत्पन्न रस को शांत रस कहा गया है।

(10) वात्सल्य रस (vatsalya ras)

शिशुओं के सौंदर्य उनके क्रिया कलापों आदि को देखकर मन उनकी ओर खींचता है। जिससे मन में स्नेह उत्पन्न होता है, वह वात्सल्य रस कहलाता है।

अधिकतर आचार्यों ने वात्सल्य रस को श्रृंगार रस के अन्तर्गत मान्यता प्रदान की है, परन्तु साहित्य में अब वात्सल्य रस को स्वतन्त्रता प्राप्त हो गयी है। 

यसोदा हरि पालने झुलावै।

हलरावैं दुलरावैं, जोइ-सोई कछु गावैं । 

जसुमति मन अभिलाष करैं।

कब मेरो लाल घुटुरुवन रेंगैं, 

कब धरनी पग द्वैक घरै।

यहाँ पर यशोदा के कृष्ण को पालने में झुलाने, उसे देखकर गाना गाने और उससे स्नेह करने को वात्सल्य रस कहा गया है।

(11) भक्ति रस (Bhakti Ras)

जब आराध्य देव के प्रति अथवा भगवान् के प्रति हम अनुराग, रति करने लगते हैं अर्थात् उनके भजन-कीर्तन में लीन हो जाते हैं तो ऐसी स्थिति में भक्ति रस उत्पन्न होता है। उदाहरण-

जाको हरि दृढ़ करि अंग कर्यो। 

सोइ सुसील, पुनीत, वेद विद विद्या-गुननि भर्यो। 

उतपति पांडु सुतन की करनी सुनि सतपंथ उर्यो । 

ते त्रैलोक्य पूज्य, पावन जस सुनि-सुन लोक तर्यो। 

जो निज धरम बेद बोधित सो करत न कछु बिसर्यो । 

बिनु अवगुन कृकलासकूप मज्जित कर गहि उधर्यो। 

इस वाक्य में आपने देव , आराध्य शिव के लिए भक्त की भक्ति को दर्शाया गया है, जो भक्ति रस का कार्य कर रहा है।

अधिकतर पूछे गए प्रश्न 

1.रस क्या होता है? 

उत्तर: ‘रस’ शब्द रस् धातु और अच् प्रत्यय के संयोग से बना है। काव्य को सुनने या पढ़ने में उसमें वर्णित वस्तु या विषय का शब्द चित्र में बनता है। इससे मन को अलौकिक आनंद प्राप्त होता है। इस आनंद और इसकी अनुभूति को शब्दों में व्यक्त नहीं किया जा सकता, केवल अनुभव किया जा सकता है, यही काव्य में रस कहलाता है। 

2.रस के अंग कितने होते हैं?

उत्तर: रस हिंदी व्याकरण के 4 अंग होते हैं-

 (1) स्थायी भाव

(2) विभाव

(3) अनुभाव

(4) संचारी भाव

3.रस के कितने भेद हैं?

उत्तर: रस के ग्यारह भेद होते है- 

(1) श्रृंगार रस

 (2) हास्य रस

 (3) करुण रस 

(4) रौद्र रस

 (5) वीर रस

 (6) भयानक रस

 (7) वीभत्स रस

 (8) अद्भुत रस

 (9) शांत रस

 (10) वत्सल रस 

 (11) भक्ति रस।

4. रौद्र रस का स्थाई भाव क्या है?

उत्तर: रौद्र रस का स्थाई भाव ‘क्रोध’ है।

5. श्रंगार रस का स्थाई भाव क्या है?

उत्तर: श्रंगार रस का स्थाई भाव ‘रति’ है।

Introduction

When a number (n) is multiplied three times, the result is known as the cube of that number. As a result, the cube of the number (n) is \({n^3}\) or n-cubed. Select the number 4 as an example. We already know that . As a result, 64 is known as the cube of 4. The cube root of a number, on the other hand, is the inverse of the cube of a number and is denoted by \(\sqrt[3]{{}}\) In the same example, 4 is called the cube root of 64. Let’s go ahead and learn more about the numbers’ cubes and cube roots.

What is a cube of a number?

A cube number is an outcome of multiplying an integer by the same integer three times. They also go by the name “perfect cubes,” or cube numbers. For example, \(4 \times 4 \times 4 = {4^3} = 64\). A  number multiplied by the same number three times is called a cube number, or a number with the exponential power of three. Because a negative number produces a negative number when it is multiplied by the same negative number three times, cube numbers of positive numbers are positive, while cube numbers of negative numbers are negative. For example, \({\left( { – 6} \right)^3}\)

In geometry, a cube’s volume is equal to the product of its length, breadth, and height. The length, breadth, and height are all equal inside the cube because it is a cube. The cube’s volume is therefore equal to , which  is its length, height, and width. This implies that a cube’s volume is a cube number.

What are the cube roots?

When we hear the word cube root, the first two words that come to mind are cube and roots. In this sense, the concepts are somewhat similar; “root” refers to the primary source of origin. As a result, we only need to consider “which number’s cube must be chosen to get the given number.”

In a nutshell, the cube root of any number is the factor that is multiplied three times to obtain the specific values. Keep in mind that a number’s cube root is the inverse of the number’s cube.

Cube roots by prime factorization

The prime factorization method can be used to calculate the cube root of a number. Begin by determining the prime factorization of a given number to find its cube root. Then, divide the obtained factors into groups, each having three identical factors. Then, to get the answer, eliminate the symbol of the cube root and multiply the factors. If any factor remains that cannot be equally divided into sets of three, the given number isn’t a perfect cube, and we cannot determine its cube root. 

Example: How to determine the cube root of 10648.

 

\(\begin{array}{l}\sqrt[3]{{10648}} = \sqrt[3]{{2 \times 2 \times 2 \times 11 \times  \times 11 \times  \times 11}}\\\;\;\;\;\;\;\;\;\;\;\; = 2 \times 11 = 22\end{array}\) 

Cube roots by estimation

If a number has several digits, it will be difficult for you to use the prime factorization and long division methods to compute the square and cube roots of the number. You will thus attempt to estimate the cube root and square root values for these numbers. Factorization becomes challenging as the number of digits rises. Estimating a square root and a cube root in such circumstances is a wise move.

The following step can be used to determine a large integer’s cube root using the estimation method if it is claimed that the provided number is a perfect cube.

Step 1: Starting with the rightmost digit, create a group of three digits starting with any cube number, such as 19683, whose cube root needs to be found.

Step 2: The unit’s digit of the necessary cube root will be provided by the first group. Since the unit digit is 3, we need to find the cube root of the cube which also has unit digit 3, i.e., \({7^3} = 343\) has unit digit 3. Hence, our unit digit for the cube root is 7.

Step 3: Now take the second group, i.e., 19, and find the cube root that is just smaller than 19 ( second group ).

\({2^3} < 19 < {3^3}\).

8 or  is just smaller than 19 hence our tenths place digit is 2.

Hence, the cube root of 19683 is equal to

\(\sqrt {19683}  = 27\)

Solved examples

Example 1: Determine the following:

1. \(\sqrt[3]{{729}}\)

Solution: We will be using the prime factorization method.

From it, we will get

Now operate both the sides under the cube root.

\(\begin{array}{l}\sqrt[3]{{729}} = \sqrt[3]{{3 \times 3 \times 3 \times 3 \times 3 \times 3}}\\\;\sqrt[3]{{729}} = 3 \times 3 = 9\end{array}\)

2. \(\sqrt[3]{{1728}}\)

Solution: We will be using the prime factorization method.

From it, we will get

Now operate both the sides under the cube root.

\(\begin{array}{l}\sqrt[3]{{1728}} = \sqrt[3]{{2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 3 \times 3 \times 3}}\\\;\sqrt[3]{{1728}} = 2 \times 2 \times 3 = 12\end{array}\)

3. \(\sqrt[3]{{2744}}\)

Solution: We will be using the prime factorization method.

From it, we will get

Now operate both the sides under the cube root.

\(\begin{array}{l}\sqrt[3]{{2744}} = \sqrt[3]{{2 \times 2 \times 2 \times 7 \times 7 \times 7}}\\\;\sqrt[3]{{2744}}\; = 2 \times 7 = 14\end{array}\)

Example 2: Determine the cube root of 59319 using estimation.

Solution:

The given number is 59319

First, we have to make the group of three from the right side. So we have the first group (319) and the second group (59).

To find the unit digit of the cube root, we have to find the cube that has the unit digit equal to the unit digit of the first group.

\({9^3} = 729\)

The cube of 9 has the unit digit 9, so our unit digit of the cube root is 9.

Now take the second group 59 and find the cube root that is just smaller than 59.

\({3^3} < 59 < {4^3}\).

27 or \({3^3}\) is just smaller than 59, hence our tenth place digit is 3.

Hence, the cube root of 59319 is equal to

\(\sqrt {59319}  = 39\)

Summary

When we hear the word cube root, the first two words that come to mind are cube and roots. In this sense, the concepts are somewhat similar; “root” refers to the primary source of origin. As a result, we only need to consider “which number’s cube must be chosen to get the given number.” The cube root of any number is the factor that is multiplied three times to obtain the specific values. Keep in mind that a number’s cube root is the inverse of the number’s cube.

When we say n is a cube root of m, then we can denote it as \(\sqrt[3]{m} = n\), with a small 3 written on the top left of the sign. The radical sign \(\sqrt[3]{{}}\)  is used as a cube root symbol for any number. Another way to express cube root is to write 1/3 as a number’s exponent. In cube roots, negative values are allowed, unlike in square roots,

For example, \(\sqrt[3]{{ – 216}} =  – 6\)

If you’re struggling with the concept of finding the cube root of a number, don’t worry – we’re here to help! Check out our video lesson no. 15 in 88guru’s online Math tuition for 8th class students.

Frequently Asked Questions

1. State the definition of cube root.

Ans: The cube root of any number is the factor that is multiplied three times to obtain the specific values. Keep in mind that a number’s cube root is the inverse of the number’s cube.

2. How is a cube root different from a square root?

Ans: A cube root is a number that when cubed yields the wanted number, whereas a square root yields the wanted number when squared. Furthermore, in cube roots, negative values are allowed, unlike in square roots.

3. What is the name of the method used for finding cube roots?

Ans: The prime factorization method is used to calculate the cube root of a number.

4. What is the cube root of 125?

Ans: 125 is a perfect cube, and 5 is the cube root of 125.

5. How Can a Cube Root Be Simplified?

Ans: The prime factorization method can be used to simplify the cube root. First, prime factorize the given number and then extract the common factors in groups of three. To find the answer, multiply these common factors by two.

Introduction

The three dimensions of a cuboid are known as the length, breadth, and height, and the volume of the cuboid depends on these parameters. As is the norm, the volume is measured either in cubic units of length like \({cm^3}\), \({m^3}\),  etc., or we can measure the volume in units of litres and millilitres. The choice is a matter of convenience.

What is a Cuboid

A cuboid is a solid rectangular box with six faces, all of which are rectangles. The rectangles that lie opposite to each other are parallel while those that are adjacent intersect each other at right angles. You can think of a cuboid as a solid rectangle in three dimensions. The figure given below illustrates it better.

A cuboid

The cuboid shown above has six rectangular faces denoted as a, b, c, d, e, and f. The front and back faces, a and b respectively, are congruent rectangles that are parallel to each other. Likewise, the top and bottom faces, c and d respectively, lie parallel to each other and are congruent, just as the side faces e and f are parallel to each other.

What is the volume of a Cuboid?

As previously mentioned, the volume of a cuboid measures the space it occupies in three-dimensional space and is dependent on its dimensions. For a cuboid, the volume is simply the product of its length, breadth, and height. That is,

𝑉=𝑙𝑒𝑛𝑔𝑡h ×𝑏𝑟𝑒𝑎𝑑𝑡h× h𝑒𝑖𝑔h𝑡  

This volume can be measured in any unit of volume like \({cm^3}\), litres, millilitres, etc. The figure given below shows the 3 dimensions.

Cuboid dimensions

Notice how this formula also means that the volume equals the area of the base times the height of the cuboid. Thus, calculation of the area of a cuboid is a fairly easy task. However, it must be noted that the units must be consistent while performing any calculations. If the dimensions aren’t provided in the same units, we can end up with skewed and wrong results.

Also Read: How to Calculate the Volume of a Sphere

Solved Examples

1. A cuboid has dimensions 10 cm x 5 cm x 4 cm. Find its volume.

Solution

Given length = 10cm, breadth = 5cm, and height = 4cm.

We have the formula for the volume, which says that 𝑉=𝑙𝑏h 

. And since all measurements are provided in cm3 only, no unit conversions are required. Therefore,

𝑉=𝑙𝑏h 

𝑉=10×5×4 

𝑉=200  \({cm^3}\)

Therefore, the volume of the cuboid is 200 \({cm^3}\).

2. Given a cuboid with length, breadth, and height of 7m, 300cm, and 2m respectively, find its volume in cubic metres.

Solution

Given length = 7m, breadth = 300cm, and height = 2m, we need to calculate the volume. However, this time, one of the dimensions is provided in centimetres instead of metres and we will need to convert it before applying the formula. We know that

1 𝑚=100 𝑐𝑚 

∴300 𝑐𝑚=3 𝑚 

Now we can apply the formula we have.

𝑉=𝑙𝑏h 

𝑉=7×3×2 

𝑉=42  \({m^3}\)

Word Problems

1. How much water can be poured into a cuboidal tank that is 6m long, 5m wide, and 3m high?

Solution 

Given length = 6m, breadth = 5m, and height = 3m. All units are consistent, and we can directly apply the formula. Thus,

𝑉=𝑙𝑒𝑛𝑔𝑡h× 𝑏𝑟𝑒𝑎𝑑𝑡h × h𝑒𝑖𝑔h𝑡 

𝑉=6×5×3 

𝑉=90 \({m^3}\)

Therefore, the volume of the tank is 90 \({m^3}\).

Summary

This tutorial discussed the cuboid shape and its volume. We learned that the volume of a cuboid is simply the product of its dimensions, which include the length, breadth, and height.

Frequently Asked Questions

1. What is the shape of the face of a cuboid and how many faces does a cuboid have?

A cuboid is a solid rectangle, and it has six faces. Pairs of opposite faces are congruent to each other.

2. What is the difference between a cube and a cuboid?

A cube is a special type of cuboid whose length, breadth, and height are all equal, i.e., it has square faces. On the other hand, a cuboid has rectangular faces with differing length, breadth, and height.

3. What is the difference between the volume of a cube and the volume of a cuboid?

There isn’t much difference in the way volumes are calculated for the cube and the cuboid. In fact, the formula for the volume of a cube is 𝑉= \({a^3}\)

, which is basically the same as that for the cuboid since here, the length, breadth, and the height are all equal to a.

4. How many sides, faces, and vertices are there in a cuboid?

A cuboid has 12 sides, 6 faces, and 8 vertices.

Introduction

A sphere is a three-dimensional object which has a circular cross-section everywhere, and its volume is the space it occupies. This volume is determined by the radius of the sphere and is measured in cubic units. You can find a large number of practical examples of spherical objects, which include cricket balls, basketballs, volleyballs, and so on.

What is a Sphere

A sphere is a three-dimensional solid figure that has a round shape and every single point on the surface is equidistant from its centre. The distance between the centre and any point on the surface is known as the radius and commonly denoted by “r”. Owing to its unique shape, the sphere is one of the very few shapes in geometry that have no edges or vertices. Depending upon the way the sphere is created, we can classify it into solid sphere or a hollow sphere.

Sphere

The image above shows a sphere with a few cross-sectional areas, and we can notice that when sliced in any direction, we get a circle. In fact, if viewed in two dimensions, a sphere would look just like a circle. The main difference is that a sphere is a three-dimensional figure and thus, has a specific volume. On the other hand, a circle is two-dimensional and has no volume. The figure below shows a sphere with its centre and radius marked, along with a point on its surface.

Sphere

What is the volume of a Sphere?

Solid Sphere

The sphere occupies a finite amount of space in the three-dimensional space. This is measured by its volume, and it depends upon how large the sphere is, or in other words, the radius of the sphere.
The formula for calculating the volume of a sphere is given by:

\(V = \frac{4}{3}\pi {r^3}\)

Here, r represents the radius of the sphere, which is half of its diameter. π is a universal constant whose value is approximately equal to 3.14. In terms of the diameter, we can write the volume as

\(V = \frac{1}{6}\pi {d^3}\)

The above formula also shows us that the volume of the sphere depends on the third power of the radius. This means that even a slight increase in radius will drastically increase the volume of the sphere. Mathematically, we can write that

\(V\alpha {r^3}\)

Volume of Hollow Sphere

The formula we just saw was valid for a solid sphere. However, we can also have a hollow sphere, which is a solid sphere from which, a smaller sphere has been taken out and we are left with a shell. In that case, we can simply subtract the volume of the sphere that was taken out. Let R be the outer radius of the sphere and r be the inner radius. We can then write

\((V = \frac{4}{3}\pi ({R^3} – {r^3})\)

Solved Examples

1. Calculate the volume of a sphere of radius 5 cm.

Solution

We are given that the radius is r = 5cm. The volume of a sphere is given by the formula

\(V = \frac{4}{3}\pi {r^3}\)

Hence, we have,

\(\begin{array}{l}V = \frac{4}{3} \times 3.14 \times {5^3}\\V = 523.59c{m^3}\end{array}\)

2. A hollow sphere is constructed such that its inner and outer radii are 3cm and 5cm, respectively. Find its volume.

Solution

Given that the radius of the inner sphere r = 3cm. The volume of a hollow sphere is given by the following formula:

\(V = \frac{4}{3}\pi ({R^3} – {r^3})\)

Here, R = 5 cm. Therefore, we have

\(\begin{array}{l}V = \frac{4}{3} \times 3.14 \times ({5^3} – {3^3})\\V = \frac{4}{3} \times 3.14 \times (125 – 27)\\V = \frac{4}{3} \times 307.72\\V = 410.3c{m^3}\end{array}\)

Hence, the volume of the hollow sphere \( = 410.3c{m^3}\).

Hence, the volume of the hollow sphere \( = 410.3c{m^3}\).

Word Problems

1. How much air can a spherical balloon of radius 7m hold without bursting?

Solution

Given that the radius of the sphere, r = 7m. The balloon can only hold as much air as its volume before it bursts. Thus, our job is to find its volume. We know that

\(\begin{array}{l}V = \frac{4}{3}\pi {r^3}\\V = \frac{4}{3} \times 3.14 \times {7^3}\\V = 1436.7{m^3}\end{array}\)

Thus, the balloon can hold a maximum of \(1436.7{m^3}\) of air without bursting.

Summary

This tutorial discussed the basics of sphere, and we developed an understanding of its volume by solving a few examples and word problems.

Frequently Asked Questions 

1. Why isn’t it possible to calculate the volume of a circle?

A circle is a two-dimensional shape that has no defined volume. The space it occupies is given by its surface area and we have no defined volume for a circle.

2. The volume of a sphere depends on which dimensions of the sphere?

The volume of the sphere \( = \frac{4}{3}\pi {r^3}\), so the volume of a sphere depends on only the radius of the sphere. The volume of the sphere ∝ the radius of the sphere

3. Given two spheres of different radii, what would be the ratio of their volumes?

Since the volume of a sphere depends in its radius raised to the third power, the ratio of the spheres’ volumes would be equal to the ratio of the cubes of their radii. That is,

\(\frac{{{V_1}}}{{{V_2}}} = {\left( {\frac{{{r_1}}}{{{r_2}}}} \right)^3}\)

Introduction

The question of how aeroplanes stay up in the air has a very interesting answer. The physics behind it isn’t so complicated and can be easily understood if you understand what aerofoils are.

To understand aerofoils, one must first understand what forces aid in keeping aeroplanes up. There are four such forces known as drag, thrust, weight, and lift. The last one of these is what allows aeroplanes to take off into the air and thus, is the most interesting to understanding. 

Lift is generated when an object travels through air and “pushes” its surrounding molecules to make way for itself. This “pushing” action causes the object to experience aerodynamic force. Physically, this aerodynamic force may be resolved into two components, which are termed drag, and lift. These components act exactly as their name describes, i.e., the effect of lift is to “lift” up the object, while the effect of drag is to slow down its motion. From this basic introduction, it is easy to see that an object can only take off and fly when the lift is greater than the drag. Aerofoils make this balance possible. Let us discuss in detail.

What is Aerofoil? 

The word aerofoil does not refer to a single object. Instead, it refers to the cross-sections of special kinds of shapes which can generate the most favourable ratio between lift and drag forces. A few common types of aerofoils are shown in the image below and you can see how these shapes aren’t straight.

Aerofoil examples

The idea behind aerofoils is to maximize efficiency. It is not possible for any object to travel without experiencing drag force. However, aerofoils are designed so that they maximize lift while minimizing drag. What’s interesting, though, is the fact that aerofoils aren’t necessary for aeroplanes to fly. An aeroplane with flat plate wings can also theoretically take off, but the efficiency would be extremely low. This is what makes aerofoils so useful while designing aeroplanes.

Aerofoil Terminology

There are a few important terms, the understanding of which, is necessary for understanding the working of an aerofoil. The image below shows these terms and they are summarized below:

Aerofoil terminologies

1. Leading edge: Just as the name suggests, the leading edge is in the “lead”. That is, it collides with the air molecules first.
2. Trailing edge: This is the “tail” of the aerofoil and is the rear-most part.
3. Chord line: When we draw a straight line from the leading to the trailing edge, we get the chord line. Its length is known the chord and depending upon the shape of the aerofoil, it can even lie outside the aerofoil.
4. Angle of attack: When an aerofoil moves through the air, it “attacks” or “cuts” through air particles. The angle of attack is the angle made by the direction of the wind and the chord line. Take a look at the diagram for a better understanding.
5. Upper surface: While travelling through air, the upper portion of the aerofoil, experiences lower pressure and the air above it travels at a higher velocity. Thus surface is known as the upper or suction surface.
6. Lower surface: The pressure underneath the aerofoil is higher and thus, the bottom part of the aerofoil marks the lower or pressure surface.
7. Camber line: This line demarks the “center” of the aerofoil and divides it into upper and lower halves. The camber line may be curved depending on the aerofoil’s shapes and its distance from the chord line is a parameter known as the camber.

How does Aerofoil produce lift?

Air flow around aerofoil

The image above shows an aerofoil moving through air and the arrows represent the flow of air. You will notice that air particles tend to follow the same path as the shape of the aerofoil. When aerofoils have a curved shape, the air molecules follow that curved path as well.

When the angle of attack is properly adjusted, the curved flow of the air makes it so that upon collision with the aerofoil, a larger number of air molecules go underneath the aerofoil than above it. This naturally creates a pressure difference between the upper and lower surfaces of the aerofoil, which makes the air below it push it upwards. This pushing force is what we call lift. The curved shape of the aerofoil also minimizes the drag, allowing aerofoils to achieve take off very easily. 

Lift Coefficient

The lift coefficient relates the lift generated by the aerofoil to its area, as well as the velocity and density of the medium the aerofoil is travelling in. It is a dimensionless quantity which is larger when lift achieved is larger, and smaller otherwise.

The following equation sets up the lift coefficient.

Here:

We can derive lift coefficient from it and arrive at the following result.

Where q is the pressure of the fluid. The value of lift coefficient is derived experimentally and it summarizes exactly how the lift generated will depend on various factors.

Types of Aerofoils

We classify aerofoils into two categories based on geometry:

1. Symmetrical Aerofoil

A symmetrical aerofoil

When the upper and lower surfaces of the aerofoil are congruent, it is termed as a symmetrical aerofoil. In such aerofoils, the chord line and the camber line coincide and perfectly divide the aerofoil into equal halves. They are generally used in helicopter blades and produce no lift if the angle of attack is zero.

2. Non-symmetrical Aerofoil

A symmetrical aerofoil

As can be seen from the image above, non-symmetrical aerofoils have unequal upper and lower halves. The chord and camber lines are separated from each other and the latter is curved. While such aerofoils can even work with zero angle of attack, they aren’t very economical.

Summary

Lift, thrust, drag, and weight are important forces which come into play when aeroplanes fly. Lift and drag are connected to each other and in fact, are components of the aerodynamic force that an object experiences while moving through a gluid. Lift pushes the object up, and drag slows it down. Aerofoils refers to cross-sections of shapes that are designed to maximize lift and minimize drag. This happens because aerofoils push a larger amount of air beneath them, leading to a pressure difference. They are classified into symmetrical and non-symmetrical types depending on geometry, and non-symmetrical aerofoils are more efficient but less economical.

 

Frequently Asked Questions

1. Who designed and invented aerofoils?

Max Munk, a German mathematician, first envisioned aerofoils. Later, Hermann Glauert made improvements to their design in the 1920s.

2. Where are aerofoils used?

Aerofoils are used in the wings and rotors of all aircrafts and helicopters. Wind turbines also have an aerofoil shape and the aeronautics sector makes the most use of aerofoils.

3. What is the significance of the four forces that aid an aircraft to fly?

An aircraft’s weight pushes it downwards, while thrust moves it forward. Drag slows it down and lift pushes it upwards. All four forces must be considered when studying aircraft.

4. At what angle of attack is the maximum lift force generated?

The maximum lift force is generated at the critical or stall angle of attack. This angle varies based on various factors, but for most aerofoils, it is between 15-20 degrees.

5. Is the concept of aerofoils applicable in liquids too?

Yes. The principles remain similar when an object moves through a liquid, but in that case, the term hydrofoil is used instead of aerofoil.

Introduction

The accelerometer is a device used to measure the acceleration of an object. The sensors present in an accelerometer allow us to measure and analyse both linear as well as angular acceleration. This device has a wide range of applications in our day to day life and forms a vital component of numerous basic systems and devices. 

An accelerometer measures acceleration forces in terms of the “g” unit, and can perform measurements in one, two, or three planes. It can also trigger a response or alarm if a certain threshold is exceeded. There are three main types of accelerometers: capacitive, piezoelectric, and piezoresistive. Accelerometers are most commonly used in guidance systems and inertial navigation.

What is an Accelerometer?

An accelerometer is a device used to measure and analyse linear and angular acceleration. It is a crucial component for many systems and devices in various aspects of our lives. Acceleration forces can be categorised into two types: static and dynamic.  Static forces, such as friction and gravity, are forces that are continuously applied to an object. Dynamic forces, which are also known as moving forces, are forces that are applied at different rates. One common example could be the vibration of a string. 

In vehicles, accelerometers are used in collision safety systems and can detect rapid deceleration. When a dynamic force is detected, the accelerometer sends an electronic signal to an embedded computer, triggering the deployment of airbags.

How does an Accelerometer work?

• The accelerometer operates on a simple principle: it measures acceleration forces and takes readings in one, two, or three planes. 
• A routine can be triggered once a threshold is exceeded, allowing us to develop smart devices. 
• A 3-axis accelerometer is the most commonly used type of accelerometer. It consists of three separate accelerometers that measure acceleration in the X, Y, and Z planes. 
• The OKYSTAR OKY3230 is a common example of such an accelerometer which, when in a stable position with no external acceleration, will only measure the force of gravity. 
• If a 3-axis accelerometer is positioned such that the X axis points to the left, the Y axis downward, and the Z axis forward, it will provide the following readings.

X = 0g

Y = 1g

Z = 0g

Accelerometer chip

Types of accelerometers

An accelerometer is a device used for measuring the rate of change in an object’s velocity. It uses an electromagnetic sensor to monitor the object or determine its position in space. An accelerometer can measure both static and dynamic acceleration. 

The three main types of accelerometers are:

Capacitive accelerometer: The Capacitive Accelerometer operates on the principle of measuring the change in electrical capacitance to determine the acceleration of an object. Here are a few salient features:

• This is the most widely used accelerometer type, and is considered to be the least expensive and compact in comparison to the other types.
• It is a micro-electromechanical system, composed of components ranging from 1 to 100 micrometres. 
• The working of the accelerometer is based on the displacement of a known mass suspended on springs, where one end of the spring is attached to the mass and the other end is attached to the capacitor.
• Any force experienced by the sensor results in the movement of the mass, causing a change in the distance between the capacitor plates, thereby altering the capacitance. 
• However, it is to be noted that the accuracy of this accelerometer is lower for high amplitude signals and frequencies compared to the other types.

Accelerometer chip

Piezoelectric accelerometer: The Piezoelectric accelerometer measures acceleration by utilising the piezoelectric effect. A few important points to note about it are given below:

• This type of accelerometer is based on a principle that is similar to that of the piezoresistive one. The material, typically PZT, undergoes deformation when subjected to acceleration, causing a change in the electric charge.
• Piezoelectric accelerometers offer high sensitivity and accuracy, making them useful for advanced seismic estimation, crash and impact tests, and other applications that require accurate measurements. 
• They can be employed in a wide range of implementations due to their exceptional performance characteristics.

Piezoelectric accelerometer

Piezoresistance accelerometers: These accelerometers are based on the change in resistance of their components when undergoing acceleration.

• The sensitivity of these devices is dwarfed by that of piezoelectric ones.
• The piezoresistive effect is the change in electrical resistivity of a material when mechanical stress is applied. The accelerometer is able to convert this change in resistance into an electrical signal.
• While the measuring range is high for this type of accelerometers, and we can measure slow-changing signals, they must be kept at a steady temperature and cannot perform well with small signals or changes.

Purpose of accelerometer

An accelerometer in vehicles measures acceleration, which is produced by motion or gravity. Its main task is to convert mechanical motion into electrical signals.

Applications of accelerometer

An accelerometer is a device that can measure acceleration of a body. Its range of application is enormous and the most common example is in inertial navigation. Some other common uses are:

• Airbag deployment in automobiles uses accelerometers.
• It can measure seismic activity and inclination.
• The depth of CPR chest compressions may also be measured via accelerometers.
• Accelerometers are used as orientation sensors in smart devices, allowing for auto rotation.
• A large number of modern electronic devices utilise accelerometers.

Summary

An accelerometer is a device for measuring linear and angular acceleration by analysing force. It operates based on a simple principle and can take measurement in one, two, or three planes. Accelerometers can be classified into three main types: capacitive accelerometers, piezoelectric accelerometers, and piezoresistance accelerometers. The number of uses of accelerometers in science and industry are enormous and the most common use is for the aircraft or the missiles in the inertial navigation systems.

 

Frequently Asked Question

1. What is a gravimeter?

An accelerometer configured specifically for the measurement of gravity is known as a gravimeter.

2. What is the most common use of accelerometers?

Aircrafts, missiles, and navigation systems make the most use of accelerometers.

3. What are MEMS accelerometers?

These are accelerometers that can detect changes in the mico-scale. The acronym corresponds to micro-electro-mechanical systems and these accelerometers are used in a large number of devices.

4. How can an accelerometer be used for hard drive protection?

Ans: If a hard drive undergoes excessive stress or vibration, an accelerometer can detect it and protect the data by separating the reader head from the disc. This prevents scratches and data corruption.

5. What are the key characteristics we need to keep in mind while selecting an accelerometer?

Ans: The bandwidth of the sensor, its sensitivity, frequency response, and the dynamic range are the most important characteristics while choosing an accelerometer for a particular use-case.

Introduction

It is important to understand prime numbers before we start figuring out how to find them. Numbers with only two factors, i.e., 1 and the number itself, are known as prime numbers. When we are given a number that is small, it is easy to figure out whether it is a prime number or not. However beyond two digits, the task becomes difficult and we have different tricks and theorems one can use.

In this article, we will discuss prime numbers as well as their identification, the consecutive prime formula, and also solve a few problems so you can better understand this concept.

What are prime numbers?

For a number to be prime, it should be a whole number divisible only by 1 or by itself. For instance, if we try to find the factors of 89, we will see that it is not divisible by any number other than 1 or itself and thus, is a prime number.

Here are a few properties of prime numbers:

• Any positive integer larger than 2 can be written as the sum of two prime numbers.
• Two prime numbers are always coprime.
• The only even prime number is 2 and all the remaining prime numbers are odd.
• The prime factors of each composite number are distinct.

How to identify if a number is prime

Since a prime number is only divisible by one or itself, an easy check for smaller numbers is to factorise them and check whether they have other factors. This involves the following steps.

Step 1: Find out the factors of the number in question.

Step 2: Determine how many does factors it has.

Step 3: If there is a total of more than two factors, the number isn’t prime.

For instance, 85 has a number of factors and as soon as you encounter the fact that it is divisible by 5, it is no longer prime. However, this method is not suitable for larger numbers since it becomes very time-consuming.

Let’s check 95 now. This time, we will utilise a clever trick that works as follows:

Step 1: Find the square root of the number given. In this case, it is \(\sqrt {95}  = 9.74 \approx 9\)  (we take the integer value).

Step 2: Select all prime numbers below the answer we have just derived (9) and see if they divided the number we are given.

Step 3: Upon doing so, we discover that 95 is divisible by 5 and thus, it is not a prime number.

Consecutive prime formula

While there is no general formula for giving us consecutive prime numbers, we can utilise a few tricks:

• Except for the 2 and 3, all prime numbers can be represented in the form \(6n \pm 1\), where n is a natural number.
• For prime numbers greater than 40, the following formula holds: Let n = 0, 1, 2,….., 39, then \({n^2} + n + 41\) gives us prime numbers.

Solved Examples

Example 1: Is 23 a prime number?

Solution:  To check whether 23 is prime or not, we have two approaches:

Approach 1:

We can check whether it fits on the pattern of \(6n \pm 1\). If we put n = 4, we get \(6n – 1 = 23\) and thus, we can say it may be prime.

Approach 2:

We can factorise 23 and we see that it only has the factors 1 and 23. Thus, both approaches confirm that it is a prime number.

Example 2: Is 61 a prime number?

Solution: For prime numbers greater than 40, we use the formula we just discussed. Let \({n^2} + n + 41\), where n=0,1,2….,39

Upon solving, we find that if n = 4, we get the answer as 61 and thus, 61 is a prime number.

Example 3: Check whether 24 is a prime number.

Solution: We start by finding its prime factors

\(\begin{array}{l}\begin{array}{*{20}{l}}{24{\rm{ }} = {\rm{ }}1{\rm{ }} \times {\rm{ }}24}\\{24{\rm{ }} = {\rm{ }}2{\rm{ }} \times {\rm{ }}12}\\{24{\rm{ }} = {\rm{ }}3{\rm{ }} \times {\rm{ }}8}\end{array}\\24{\rm{ }} = {\rm{ }}4{\rm{ }} \times {\rm{ }}6\end{array}\)

Thus, 24 has numerous factors, including 1, 2, 3, 4, 6, 8, and 12. Thus, it is not a prime number.

Summary

• A whole number divisible only either by one or by itself is called a prime number.
• A prime number larger than one has only one prime factor, i.e., itself.
• Any positive integer greater than 2 can be written as a sum of two prime numbers.
• Two prime numbers are always coprime.
• 2 is the only even prime number.
• The most basic way to check whether a number is prime is to factorize it. If it has more than two factors, it is not a prime number.
• All prime numbers greater than 3 can be written in the form \(\;6n \pm 1\), where n is a natural number.
• Prime numbers greater than 40 can be written in the form \({n^2} + n + 41\), where n goes from 0 to 39.

Frequently Asked Questions

1. What are prime numbers?

Numbers that can only be divided by one or by themselves are called prime numbers.

2. What is the formula to calculate prime numbers above 40?

Prime numbers greater than 40 can be written in the from \({n^2} + n + 41\), where n goes from 0 to 39.

 3. Is it possible that a number is both composite and prime?

No. The conditions of being prime and being composite are contradictory. However, the number 1 is said to be neither prime nor composite.

4. What are composite numbers?

Composite numbers are the opposites of primes. These are numbers which have more than two factors.

5. State some properties of prime nunumbers.

• Two prime numbers are always coprime.
• Any positive integer greater than 2 can be written as the sum of two prime numbers.
• A prime number is a positive integer greater than 1.
• It is only divisible by 1 and itself.
• Every prime number has exactly two distinct factors, namely 1 and the prime number itself.
• There are infinitely many prime numbers.
• The first five prime numbers are 2, 3, 5, 7, and 11.
• Every integer greater than 1 can be expressed as a product of primes, and this factorization is unique up to the order of the factors. This is known as the Fundamental Theorem of Arithmetic.
• Prime numbers are important in number theory and have applications in cryptography and other areas of computer science.

Introduction to the concept of Symmetry

The word “symmetry” is frequently utilized in daily life; instances include the symmetry of butterfly wings, architectural designs, and more. Do you recognize symmetry? When a figure can be folded into two identical halves, we say that it is symmetrical, and as a result, this phenomenon is referred to as symmetry. The line that divides a figure into two identical sections is known as the line of symmetry. In this essay, the two primary symmetries—rotational symmetry and line symmetry—will be adequately explained.

Definition of Line Symmetry and Rotational Symmetry

Line Symmetry

 Line symmetry is a type of symmetry that involves reflections. When an object has at least one line that splits a figure in half, with one half being the mirror image of the other, this is referred to as line symmetry, also known as reflection symmetry. The symmetry line might be vertical, diagonal, horizontal, slanted, etc. An imaginary axis or line that splits a figure into two identical halves is called a line of symmetry.

Rotational Symmetry 

A fixed point is the centre of many objects. A windmill, a car’s wheels, a clock’s hands, a fan’s blades, etc. are a few examples. When anything rotates, its size and shape stay the same. Rotational symmetry is the ability of a shape to retain its appearance after a revolution. Rotations can occur both in a clockwise and anticlockwise direction. A form or item that keeps its appearance after a given amount of rotation by partial turn has been applied has rotational symmetry.

Therefore, a figure is considered to have rotational symmetry if it fits onto itself more than once throughout a full rotation. A square is being spun here. No matter how it is rotated, the square appears unchanged. As a result, the square acquires rotational symmetry.

Line of Symmetry

An imaginary axis or line that can be used to divide a figure into its symmetrical halves is referred to as a “line of symmetry” in mathematics. It is often referred to as the axis of symmetry. The line symmetry is also called a mirror line because it exhibits two coinciding reflections of the same image. Consequently, it also has a form of reflection symmetry. In most cases, it splits an object in half.

Order of Rotational Symmetry

The number of distinct orientations in which a form maintains its inherent shape is related to the order of rotational symmetry of that shape. A complete turn or full turn is a rotation of \(360\)  degrees. In a full turn, there are primarily 4 rotational positions.

rotation of \(90\) degrees.

rotation of \(180\)  degrees.

rotation of \(270\) degrees.

rotation of \(360\) degrees.

Shapes of Line Symmetry and Rotational Symmetry

Now we know that some shapes have line symmetry and some have rotational symmetry. Some shapes, respectively, have rotational and line symmetry. We’ll discuss some items’ symmetry right now, which demonstrates both kind of symmetry.

Square: A square \(ABCD\) will always fit exactly onto itself when rotated through \(90\),\(180\),\(270\), and \(360\) degrees about the point \(O\). It has rotational order symmetries as a result. The diagonals and the lines connecting the middles of the opposing sides make up the square’s additional four symmetry lines.

Rectangle: A rectangle \(ABCD\) will always fit exactly onto itself if it is rotated between \(180\)and \(360\) degrees. It has \(2\) rotational order symmetries as a result. Additionally, it has two lines of symmetry.

Equilateral Triangle: An equilateral triangle ABC always fits exactly onto itself when rotated through \(120\),\(240\), and \(360\) degrees about the centroid \(O\). Therefore, the rotational symmetry is of order \(O\). The triangle additionally has three lines of symmetry along the bisectors of the internal angles.

Interesting facts

• Every single regular polygon is symmetrical in shape. If a figure’s rotational symmetry is \(180\) degrees, it has point symmetry.
• The number of sides equals the number of symmetry lines.

Solved Example

Find out the shapes from below, which do not have rotational symmetry

Solution:

1. As everyone is aware, rotational symmetry is a type of symmetry where, after rotating a shape in a certain direction, the new shape is the same as the original.
2. The preceding figure demonstrates that (b) and (a) lack rotational symmetry as a result.
3. There are more symmetric forms, such as the point, translational, gliding, reflectional, helical, etc., but they fall outside the scope of what is now known.

Conclusion

This article provided comprehensive information on line symmetry and rotational symmetry. The rotational symmetry order was also revealed to us. In addition, we discovered the shapes with rotational and line symmetry.

Frequently Asked Questions 

1. What do line symmetry and rotational symmetry mean?

If a figure is the same on both sides of a line, it is said to be symmetrical. When a figure can be rotated while keeping its original appearance, it exhibits rotational symmetry.

2. What sets lines of symmetry apart from other lines of symmetry?

The line that divides a figure into two identical sections is known as the line of symmetry. If the shape of an object stays the same when a line is drawn through the middle of it, it possesses line symmetry.

3. In mathematics, what is rotational symmetry?

A form is said to have rotational symmetry if it keeps its appearance after a revolution. Rotations can happen both clockwise and anticlockwise. An object or form’s size and shape don’t change while it rotates. Instead, it revolves around a predetermined location known as the rotating center. This phenomenon is referred to as rotational symmetry.

4. Do right triangles have symmetry along their lines?

A right-angled triangle has non-symmetrical lines. A symmetry line is absent. There is only rotational symmetry of order. The right triangle is isosceles if it only contains one line of symmetry.

Introduction

The relationship between a number and its square root is important to understand. Squaring a number means multiplying it by itself, while finding the square root of a positive number involves finding the number that, when squared, results in the original number. For example, if the square of a number p is q, then the square root of q is equal to p. 

As an example, 2 squared is 4, and the square root of 4 is either +2 or -2.

What is a square of a number?

The square of a number is defined as the product of the number with the number itself. This is represented by a superscript 2 in front of the number. Here are a few examples.

• squared is \(2 \times 2 = {2^2} = 4\)
• 3 square is \(3 \times 3 = {3^2} = 9\)
• 4 square is \(4 \times 4 = {4^2} = 16\)

Square roots

What are square roots?

The square root operation is the inverse of squaring a number. Basically, it is the number which, when multiplied by itself, gives the number whose square root we are trying to find. The square root is operated by the radical symbol \(\sqrt {} \) and the number inside the radical is called the radicand.

Hence, given a number , its square root is represented by \(\sqrt p \)  and if we square \(\sqrt p \) we arrive back at the original number. Thus,

\(\sqrt p  \times \sqrt p  = \sqrt {{p^2}}  = p\)

Square root symbol

The square root function, which is a one-one function, takes a positive number and yields its square root. If it is provided a negative number, the answer is complex.

\(f\left( a \right) = \sqrt a \)

Example: The square root of 4 is equal to \(\sqrt 4  =  \pm 2\)

The square root of 9 is equal to = \(\sqrt 9  =  \pm 3\)

The square root of 16 is equal to = \(\sqrt {16}  =  \pm 4\).

Square roots by prime factorization

We can find the square root of a number by using the prime factorisation method.

1. We start by finding out the prime factors of the number.
2. We then group the same factors into pairs of two.
3. We then take one number each from these pairs and multiply them together. The product we thus obtain is the square root we need.

Example: Find the square root of 36 by using the prime factorization method.

Upon factorising 36, we see that the prime factors come out to be

\(36 = 2 \times 2 \times 3 \times 3\)

We now group the same numbers together

\(36 = \left( {2 \times 2} \right) \times \left( {3 \times 3} \right)\)

And then take one number from each pair. The product thus obtained is the square root. Hence

\(36 = {\left( {2 \times 3} \right)^2} = {6^2}\)

Therefore, the square root of 36 is \( \pm 6\).

Square roots by estimation

In various cases, the perfect square root of a number doesn’t exist and we estimate the nearest value. This can be explained by taking the example of 24.

1. Start by finding the nearest perfect squares to 24. These are 25 and 16, whose square roots are 4 and 5.
2. Since \({5^2}\)  is closer to 24, we increase 4 to 4.5 and check again.
3. Again, \({4^2} = 20.25,So\;{5^2}\) is still closer to 24. We adjust again and go from 4.5 to 4.8.
4. This way, we continue till a close enough estimate has been made. In this case, it comes out to be 4.8989

Also read: How to Find Cube Root of a Number

Square roots by Long division method

It is a method used to find the square roots of large numbers by dividing them into parts and getting the exact value of the square root of the number.

Example: Find the square root of 150 using the long division method?

To obtain the square root of a number using long division:

1. Group the digits of the number into pairs starting from the rightmost digit. This is done by placing bars on top of the groups for easy identification.
2. Find the largest perfect square less than or equal to the leftmost pair (which is 1 here) and use its square root as the divisor and quotient (both come out to be 1). Divide the leftmost pair (1 here) by the divisor, and bring down the next pair of digits (50 here). 
3. Bring the last digit of the quotient (1 here) to the divisor (1 again) and using the sum of these two numbers (1+1=2). Now try to find the largest two digit number that starts with 2 and doubling which, will give us a number below the number we have brought down (50 here).
4. Continue the process in this way and add a decimal point in the quotient and zeroes in the dividend if required untill a desired accuracy is reached. The final quotient will become our square root.

The following table better demonstrates this:

Hence, the square root of 150 is equal to 12.247

Solved Examples

1. Find the square root of 144 via prime factorization.

When we factorise 144, we arrive at the following equation

\(144 = 2 \times 2 \times 2 \times 2 \times 3 \times 3\)

We group these factors into pairs

\(144 = \left( {2 \times 2} \right) \times \left( {2 \times 2} \right) \times \left( {3 \times 3} \right)\)

Then take one factor from each pair.

\(144 = 2 \times 2 \times 3\)

Hence, 12 is the square root of 144.

2. Estimate the square root of 30.

The nearest perfect squares are 25 and 36 and therefore, the square root of 30 must lie between 5 and 6. Since \({5.5^2} = 30.25\), the square root of 30 is very close to 5.5. We now try the guess 5.4, whose square is 29.16. To get better accuracy, let us go up to 5.45, whose square is 29.7025. Continuing this way, we get the desired answer as 5.4772.

Summary

This article discussed the following concepts:

1. What is meant by the square and square root of a number?
2. How square roots are represented.
3. Various ways of finding square roots of a number. These included prime factorization, estimation, and long division methods.

 

Frequently Asked Questions

1.What are the methods used in finding the square root of a decimal number?

The square root of a decimal number may be found via long-division or estimation methods.

2. When is prime factorization useful?

Prime factorization is only useful when the given number is a perfect square. Otherwise, it fails.

3. What are perfect squares?

Perfect squares are those numbers whose square roots are whole numbers, rather than decimal numbers.

4. How do we find square roots of numbers which aren’t perfect squares?

Estimation and long division methods can aid us in such scenarios.

Introduction

Under the right circumstances, fire can be a very helpful chemical reaction. It’s useful in a lot of situations, but it can be dangerous if it’s burned improperly. The portable gadget known as a fire extinguisher is used to put out fires of any size. People depend on fire for a wide variety of tasks. Fire is essential for many industrial processes; without it, it would be impossible to imagine things like cooking and lighting. Dry vegetation in woods has caught fire before, posing a threat to wildlife for miles around. Multiple types of fire extinguishers are used to put out the various blazes. Many various kinds of fire extinguishers are available, including those that use water and foam, carbon dioxide, dry chemicals, wet chemicals, water mist, and so on.

What is a Fire Extinguisher? 

To put out a fire, you need an extinguisher, which can contain dry carbon, water, or a chemical. It’s put to use dousing flames caused by things like cooking oil, flammable gases, petroleum, wood, clothing, paint, and so on. These are stashed in convenient, easy-to-reach locations. Classifications of fire depend on the nature of the combustible substance.

Fire Extinguisher

Explain the Principle on which a Fire Extinguisher works 

A fire extinguisher relies on the “fire triangle,” a set of interrelated concepts for its operation.

• When fighting a fire, the primary rule is to extinguish it at its origin.
• The availability of oxygen is the second essential item.
• The third component is the fuel being used in the fire.

Fire Triangle

Types of fire extinguisher

The fire extinguisher is of numerous varieties, since the fire extinguisher acts according to the source of the fire. There are seven distinct varieties of fire extinguisher, each distinguished by the chemical it contains.

1. Water and foam Based: Electric appliance, coal, paper, textile, wood, etc. fires can all be put out with a foam base fire extinguisher. Use a water-based extinguisher for flames involving metal, wood, cooking grease, and similar materials.
2. Carbon Dioxide Based: In this type of extinguisher contains carbon dioxide, which hinders the supply of oxygen and helps cool down fire. This is used for fires caused by electricity. 
3. Wet Chemical-based Extinguisher: This type of extinguisher is used for the fire caused by oils, fats, and in commercial kitchens. It removes the heat based on the fire triangle principle. 
4. Dry Powder Fire Extinguisher: A dry powder is filled in an extinguisher; it hinders the supply of oxygen to cool down the heat generated. It is used in fire caused by metals, like sodium, zirconium, etc. 
5. Clean Agent Fire Extinguisher: It contains a halogenated clean agent i.e., halogen with ozone-depleting hydrocarbons. 
6. Water Mist Extinguisher: They are used to quench fires caused by wood, paper, as well as electric appliances.
7. Dry Chemical Fire Extinguisher: It is filled with a dry chemical that interrupts the chemical reaction that is the cause of the fires

Working of Water Fire Extinguisher 

• Water extinguishers are filled with water and designed in such a way that when the seal is broken it expels the water in force to quench a fire. 
• First, the seal is broken, and the safety pin is pulled out.
• Then, the lever of the extinguisher is squeezed. 
• By squeezing the lever, it forces a pointed rod within the valve, that punctures the cylinder containing high-pressure gas. 
• The Gas-filled in the cylinder is released into the cylinder filled with water and, forces the water downward.
• Pressured water then came out of the pipe, this pressure triggered water to cool down the fire from 4 to 6 feet away. 

Preparation of Soda Acid Fire Extinguisher with diagram and explain How it works?

The Soda acid fire extinguisher is prepared with sodium bicarbonate and diluted sulphuric acid. Let’s check the process of preparation of a Soda acid fire extinguisher.

• First, we need a wash bottle with a nozzle, we fill that bottle with 20 ml of sodium bicarbonate  \(\left( {NaHC{O_3}} \right)\) solution,
• Then, we suspend an ignition tube by a thread that contains a dilute solution of sulphuric acid \(\left( {{H_2}S{O_4}} \right)\)  in the wash bottle,
• The next step is to close the mouth of the bottle, 
• After closing the bottle, we tilt the bottle in such a way that the acid-filled ignition tube reacts with the sodium bicarbonate solution, 
• After some time, we notice that there is discharge coming out of the nozzle of the bottle.
• That discharge is the of carbon dioxide \(C{O_2}\) , and other products are sodium sulphates and water.
• When we take the discharge near the fire it quenches the supply of oxygen within the fire and the fire cools down.
• The Carbon dioxide \(C{O_2}\) released during the reaction work as an extinguisher that hinders the supply of oxygen in fire and hence fire cools down.

\({\bf{2NaHC}}{{\bf{O}}_3} + {{\bf{H}}_2}{\bf{S}}{{\bf{O}}_4} \to {\rm{ }}{\bf{N}}{{\bf{a}}_2}{\bf{S}}{{\bf{O}}_4} + {\bf{2}}{{\bf{H}}_2}{\bf{O}} + {\bf{2C}}{{\bf{O}}_2}\)

Preparation of Soda Fire Extinguisher

Summary

In the above tutorial, we have studied the fire extinguisher. A fire extinguisher is a container that contains different types of elements like foam, wet chemical, dry chemical, carbon dioxide, water, water mist, etc. we must choose a correct fire extinguisher when a fire breaks out because a wrong type of extinguisher can ignite the fire more despite cooling it down. The fire is divided into five classes class A, B, C, D, and K. These are divided according to the type of material causing the fire i.e., wood, paper, electric appliance, oil, fat, metals, etc. These types of fires are quenched by different types of fire extinguishers known as Foam, water, chemical, and carbon dioxide-based extinguishers. 

 

Frequently Asked Questions: 

1. What is the difference between a rechargeable and a non-rechargeable fire extinguisher? 

Ans. Rechargeable fire extinguishers can be refilled and reused, while non-rechargeable fire extinguishers must be replaced after use. 

2. How long does a fire extinguisher last? 

Ans. The lifespan of a fire extinguisher depends on the type of extinguisher and the environment in which it is stored. Generally, fire extinguishers should be replaced every 5-10 years.

3. What is the best way to store a fire extinguisher? 

Ans. Fire extinguishers should be stored in a cool, dry place away from direct sunlight and away from any heat sources.