Blog

Introduction

A plane slanted at a particular angle is known as an inclined plane. Such a plane is connected to the ground on one end while the other end is raised by a given height that is referred to as the slant height. 

The angle of inclination for an inclined plane is defined as that angle at which an object just starts to slide down due to its own weight.

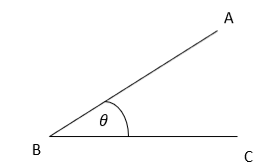Inclined plane AB

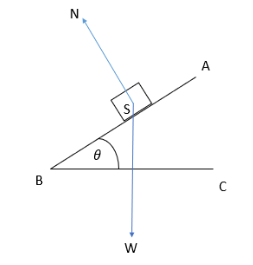
Body on an inclined plane

Normal force in inclined planes

Generally, it is observed that the normal reaction due to gravitational forces acts just opposite to the weight of the body, especially when placed on the ground. However, that is not universally true. In fact, the normal reaction in the case of an inclined plane acts in a direction that is perpendicular to the incline, not the ground.

Frictional force

Friction occurs when two surfaces come into contact and its tendency is to resist motion. Thus, it always acts opposite to the direction of motion of an object. For an object sliding down an inclined plane, frictional force acts up the incline and vice versa.

Gravitational force components

The gravitational force may be resolved into two components when dealing with an inclined plane. 

1. The normal/vertical part acts perpendicularly to the incline and downwards from it. In the diagram below, it is represented as \({W_{V}}\).
2. Similarly, there exists a horizontal component of the body’s weight that acts parallel to the incline and points downwards. It is represented by \({W_{H}}\)in the diagram.

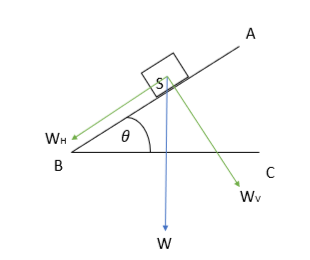
Resolution of gravitational force

The body is at equilibrium

In the diagram,

N= normal force

W= weight of the body (gravitational force)

\({W_{H}}\)=Horizontal component of the gravitational force

\({W_{V}}\)= Vertical component of the gravitational force

f= frictional force

And we are given that the body is at equilibrium. In such a case,

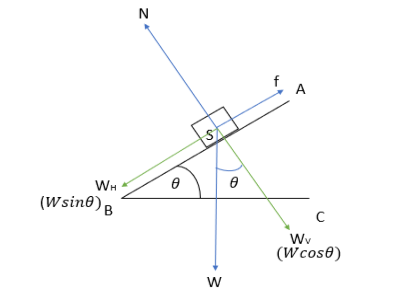
Body in equilibrium at incline

We can equate the horizontal and vertical forces. Let us start with the horizontal ones:

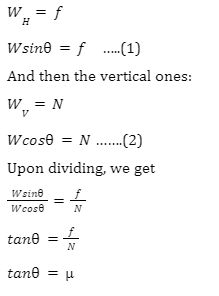
The quantity μ is known as the coefficient of friction.

Equilibrium of a body on an incline plane:

Two limiting cases of equilibrium exist on an inclined plane:

1. The body is moving up the incline or,
2. It is falling down the incline.

A body moving down the incline.

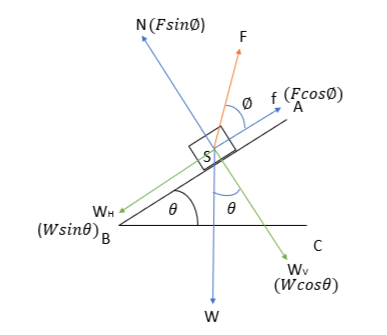
When the body moves down the incline, we have

N= normal force

W= weight of the body (gravitational force)

\({W_{H}}\)=Horizontal component of the gravitational force

\({W_{V}}\)= Vertical component of the gravitational force

f= frictional force

F= external force

Applying the conditions of equilibrium,

A body moving down the incline.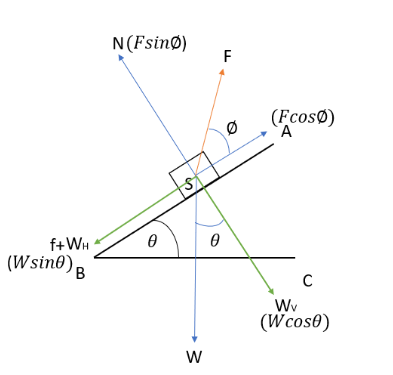

As before,

N= normal force

W= weight of the body (gravitational force)

\({W_{H}}\)=Horizontal component of the gravitational force

\({W_{V}}\)= Vertical component of the gravitational force

f= frictional force

F=external force

We proceed just as in the previous example.

Solved problems on inclined plane

1. If a block kept on an inclined plane will start slipping, find the angle of inclination given that the coefficient of static friction = 1.73.

We are given the value of = 1.73. We can use the fact that

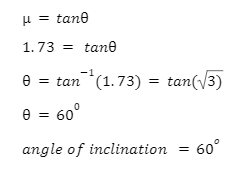
2. If a block of mass 10 kg remains at rest on an incline of\({45^{0}}\), find the force of friction. (Take\(g=10 m{s^{ – 1}}\))

Given that, the block is at rest so that net force parallel to the incline is zero.

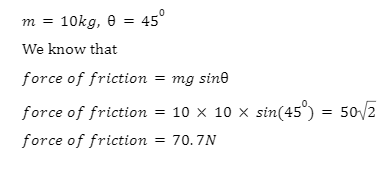
Summary

An inclined plane is a sloping surface designed to move heavy machinery and tools that cannot be lifted directly. Various types of inclined surfaces such as ramps, stairs, and slides exist. 

The primary benefit of an inclined plane is that it helps us move large objects by applying a lesser amount of force. The angle of inclination plays a critical role in determining how much force we must apply and if we would be able to move the object in question at all. For the object to not fall down back on us, we must move it up the incline at a certain angle of friction.

Frequently Asked Questions

1. How many components of gravitational force do we have on an inclined plane?

There are two components we can resolve the gravitational force into:

1. Horizontal component and,
2. Vertical component.

2. Write down two functions of an inclined plane?

Inclined plane has a large number of uses, with the primary ones being,

1. They function as simple machines.
2. They help us move heavy objects upward with ease.

3. What are the forces experienced by an object moving on an inclined plane?

The object experiences gravitational force, normal reaction, and frictional force.

4. In what direction do frictional forces act?

Frictional forces always act opposite the direction of motion of an object.

5. What is the angle of inclination?

It is that angle at which, when a body is placed on an inclined plane, it will start sliding down due to its own weight.

Introduction

A wave is defined as the propagation of a continuous disturbance across two points. They can propagate with, or without a medium in between the given points and on this basis, they are broadly classified as follows:

1. Mechanical waves: A wave that requires a medium to propagate. For sound waves cannot travel in vacuum.
2. Electromagnetic waves: These waves need no medium to travel and thus, can travel in vacuum as well. Light is a common example of electromagnetic waves. They can also be defined as a pulse of energy that traverses through vacuum or a given medium.

Waves generally travel in the form of crests and troughs and are characterised by  various factors like amplitude, velocity, frequency, etc. In simple terms, the amplitude is a measure of the energy they carry. 

Define the Amplitude of a wave

The amplitude of a wave is a measure of the energy transferred by it and is defined as the distance from the axis to the bottom or top of a peak or valley of the wave. Generally, this value is expressed in metres (m), though other measurements exist as well.  Amplitude determines how much the wave rises and falls and waves with higher amplitudes carry more energy than those with lower ones. 

Mathematically, a sinusoidal wave can be represented by the following equation:

We can define amplitude in another way. It can be understood that the amount of displacement of a particle in the wave is an indication of the energy required to create its motion. This quantity of energy is expressed as the amplitude of the wave.

Sound

Sound is a form of energy that causes objects to vibrate. It can be transferred across two locations through a medium that may be solid, liquid, or gas.  Sound waves are longitudinal in nature and thus, move in the form of compressions and rarefactions. When an object produces sound, its vibrations transfer energy to the molecules of the medium around it, which then propagate and reach our eardrums. Our ears convert these vibrations into signals that our brain can interpret as sound.  The range of sound frequencies audible to humans is 20Hz to 20KHz, and frequencies above and below this range are known as ultrasound and infrasound, respectively. 

Ultrasound waves

Ultrasonic waves mostly find use in the medical field in the diagnosis of various diseases. Processes like ultrasonography utilize ultrasounds.

Infrasonic waves

These are sound waves with frequencies below the 20 Hz mark, which are generally produced in natural phenomenon like volcanic eruptions, earthquakes, etc.

Define Amplitude in Physics?

In physics, amplitude refers to the maximum distance or displacement travelled by a vibrating body or wave from its resting point. All waves possess an amplitude and it is an important characteristic that defines waves. 

Amplitude modulation is a technique used to modulate the amplitude of a given wave.  Generally, a low amplitude wave is modulated using a carrier wave. This process allows us to transmit data across locations. Amplitude modulation has several applications such as signal transmission, radio broadcasting among others.

Characteristics of Sound

• Pitch: Pitch refers to the subjective sensation of the frequency of a sound wave. A high-frequency sound wave produces a high pitched sound, while a low-frequency sound wave produces a low pitched sound. Pitch or frequency is measured in Hertz (Hz).
• Loudness: The loudness of sound is determined by the amplitude or size of the sound wave. A larger size or amplitude corresponds to a louder sound. Loudness is measured in decibels (dB).
• Amplitude: Amplitude is the maximum displacement of the particles from their mean position as sound waves travel through the medium. It is expressed in metres.
• Wavelength: Sound is a longitudinal wave and it travels across two points via a medium in the form of compressions and rarefactions. It is characterised by a certain wavelength, which is defined as the distance between two consecutive compressions or rarefactions. Typically, these wavelengths lie between 1.7 cm to 17 metres. 

Wavelength is connected to speed and frequency of sound via the following relation:

  \[\lambda  = \frac{v}{f}\]

• Frequency: The number of compressions or rarefactions that a sound wave produces in unit time is known as the frequency of the wave. It is expressed in Hertz (Hz), which is equal to one second inverse.

  \[f = \frac{1}{T}\]   

• Time period: The time taken for the particles of the medium to undergo a complete cycle from one compression to the next is known as the time period. Time period and frequency are inversely related. Its unit is second.

\[T = \frac{1}{f}\] 

• Velocity: The velocity of the wave measures how fast the disturbance in the medium travels between two locations. It can vary depending on the medium in question and is expressed in (\(m{s^{ – 1}}\))

  Velocity=Displacement/ time

Summary

Waves are a common phenomenon that we encounter in our day-to-day lives. For instaande , the light waves produced by the sun, the waves in the ocean, and the sound waves we hear. In terms of physics, waves are a way of transferring energy via a disturbance. 

Sound waves are generated by a vibrating body that transfers energy to the molecules of the medium that surrounds it. This energy in the form of vibration then propagates through the medium. Sounds can take many forms, such as pleasant sounds, noise, music, etc. Understanding the characteristic properties of sound waves is essential for the creation of music and for other applications.

 

Frequently Asked Questions

1. State the differences between pitch and loudness?

2. Are pitch and frequency different?

Frequency is a measure of how often a particular event occurs whereas pitch is a concept that is closely related to frequency. Even though the two properties are related, there is no mathematical relation for the same. 

Note that while frequency is relevant for all types of waves, including mechanical and electromagnetic waves, the pitch is a challenging concept to define and is relevant only for sound waves.

3. What is the hearing range of the human ear?

Sound waves in the 20 Hz to 20,000 Hz regime are audible to the human ear. It might be interesting to note that while some newborns can hear slightly above the 20 kHz mark, but they lose this sensitivity with age.

4. What is the relation between wavelength, velocity, and frequency of a wave?

\[v = f\lambda \]

From the above relation, it is evident that wavelength and frequency are inversely related. Note that the frequency of a wave never changes. The velocity and wavelength increase or decrease in different media.

5. What are the three ways in which the above equation can be written?

Introduction

In 1820, Hans Oersted conducted a famous experiment using a compass needle and a current-carrying conductor. He observed that when no current was flowing through the conductor placed near the compass, the latter would always point towards the north pole. However, when the conductor was carrying a current, the needle deflected in a particular direction.

He found that the direction of deflection was tangent to a circle, which suggested that current-carrying wires produce a magnetic field around them (Figure 1). This magnetic field due to a urrent-carrying conductor can be calculated using the Biot-Savart law.

To estimate the magnetic field due to a current element, one can first calculate the differential field \(d\overrightarrow B \) and then integrate it over the loop. However, if we have a symmetry in the system, our calculations can be simplified using Ampere’s law.

Who Was André-Marie Ampere?

André-Marie Ampère, a French physicist and mathematician, displayed prodigious talents and began his study of mathematics at the early age of 12. His interest in the field of electromagnetism was sparked by Oersted’s discovery that electric currents produce magnetic fields.

Ampère expanded on Oersted’s work and demonstrated that current-carrying wires either repel or attract one another, depending on whether they were carrying current in the same or in opposite directions. One of his most significant contributions to the field is known as “Ampere’s Law” and in honor of his work, the SI unit of electric current is named after him.

Statement of Ampere’s Circuital law

Ampere’s law can be stated as follows: “The line integral of the magnetic field around any closed loop is proportional to the current passing through the loop.” If there are multiple currents passing through the loop, the algebraic sum of these currents must be taken into account and the loop considered for the calculation is called an “Amperian loop” or “Amperian coil.”

Note that the choice of the loop is aribtary and depends upon our ease of calculation.

Mathematical Form of Ampere’s Circuital Law

If we are given that a current  is flowing through a given loop C, th

\[\oint {\vec B}  \cdot \overrightarrow {dl}  = {\mu _0}{i_{enc}}\]

Line Integral of \(\overrightarrow B \) – The entire current loop can be divided into infinitesimally small subelements \(d\overrightarrow l \) . To calculate the total contribution, we simply integrate the tangential component of \(\overrightarrow B \)  across the length of the loop.

Net current \({i_{enc}}\) – This is the current that is enclosed by the loop. Note that only those currents need to be taken into account which are inside the area of the loop.

From figure  \({i_{enc}} = {i_1} + {i_2}\) only

Ampere’s circuital law

Direction of Integral – We can calculate the direction of the current and magnetic field using the right hand rule. If we curl our right hand such that our thumb points in the positive direction of current, our fingers will then point along the direction of magnetic field.

Inconsistency of Ampere’s Circuital Law

Take a look at the figure below and try to apply Ampere’s law to it. The circuit consists of a capacitor in a circuit wherein, a current \({i_c}\) is flowing. 

Ampere’s circuital isn’t always valid.

Let us take two surfaces 

1. \({S_1}\): A simple circular loop wherein, \({i_{enc}}\)  is simply \({i_{c}}\).
2. The surface \({S_2}\)which is bulged out to the right. Since no current can flow in the gap of the capacitor, \({i_{enc}} = 0\).

Thus, we arrive at a discrepancy wherein, the line integral of magnetic field is both zero and non-zero.

Modified Ampere’s Circuital Law or Ampere – Maxwell’s Circuital Law

Maxwell modified Ampere’s law to remove the aforementioned discrepancy by introducing a term known as the displacement current. It is defined as:

                                 

Where E is the electric field passing through the loop. Notice how this term vanishes when the electric field is constant in time, leading us back to the original Ampere’s law. The modified form thus becomes

                               

And the capacitor problem from before can now be solved:

Correction to Ampere’s law

This time, we notice that inside a capacitor, an electric field exists which varies in time and thus, the discrepancy has now been resolved.

Application of Ampere’s Circuital Law

There are a plethora of situations wherein, Ampere’s law comes in handy. As the first take example, let us calculate magnetic field due to a long wire at a distance r (r >> R)

The magnetic field due to current-carrying wire.

The wire has cylindrical symmetry and we create a circular Amperian loop. Using the right hand rule, the direction of magnetic field comes out to be tangential to every point on the loop and thus,

Ampere’s Law then states that

$$
\begin{gathered}
\oint \vec{B} \cdot \overrightarrow{d l}=\oint B d l=B \oint d l=B \cdot 2 \pi r=\mu_0 I \\
B=\frac{\mu_0{ }^i}{2 \pi r}
\end{gathered}
$$ 

This well-known result can also be verified via Biot-Savart law.

Solved Examples

Example 1. $$
\text {  Find the value for } \vec{B} \cdot \overrightarrow{d l} \text { in surface } 1 \text { and } 2 \text { in units of } \mu_{0^{\circ}}
$$

Ans: Loop S1 contains two currents of values 1A and 5A. Thus,

$$
\vec{B} \cdot \overrightarrow{d l}=6
$$

Similarly, S2 has two currents, but one of them is in the negative direction. Therefore,

$$
\vec{B} \cdot \overrightarrow{d l}=5-2=3
$$

Example 2: A long straight wire of 2cm radius carries a current of 10A. Find the magnetic field at a distance of 8cm from it.

Ans: Using the equation previously derived,

$$
B=\frac{\mu_0{ }^2}{2 \pi r}=\frac{4 \Pi \times 10^7 \times 10}{2 \pi  \times 8 \times 10^{-2}}=\frac{20 \times 10^{-3}}{8}=2.5 \times 10^{-5} \text { Tesla }
$$

Summary

Ampere’s law is a useful tool for estimating the magnetic field due to current distributions when the system exhibits some degree of symmetry. When time varying electric fields are present inside the loop, Ampere’s law fails to produce reasonable results. To address this limitation, Maxwell introduced the concept of Displacement current and a simple demonstration can be made using a capacitor. 

Ampere’s law is particularly useful in estimating the magnetic field due to linear current carrying wires, where the magnitude of the field is inversely proportional to the distance at which it is being calculated.

Frequently Asked Questions 

1. Apart from current carrying wires, what other sources can produce magnetic fields?

Time varying electric fields can produce magnetic fields.

2. Is ampere’s law universally true?

No. The law fails for dynamic cases and is only valid when no time-dependence exists.

3. Is it possible to derive Biot-Savart law from Ampere’s law?

Ampere’s law itself was derived using Biot-Savart law and thus, it is possible to interchange between the two.

4. For the case of electrostatics, is there a law equivalent to Ampere’s law?

Yes, Gauss’ law is almost congruent to Ampere’s law in electrostatics.

5. Summarize Ampere-Maxwell’s law?

Ampere Maxwell’s law proves how a changing electric field can produce a magnetic field, just as a changing magnetic field can induce an electric field (Faraday’s law).

Introduction

Three-dimensional (3D) shapes are solids with three dimensions: length, breadth (width), and height. The word “3D shapes” refers to three dimensions. Every 3D geometric shape takes a certain amount of space depending on its dimensions, and in daily life, we are surrounded by many 3D shapes. Cubes, cuboid forms, cones, and cylinders are a few examples of 3D shapes.

3D shape example

There are several three-dimensional (3D) shapes with various bases, volumes, and surface areas. Let’s talk about each one individually.

Sphere

A sphere has a round shape. It is a 3D geometric shape with equidistant points from its centre at every point on its surface. Though it resembles a spherical, our planet Earth is not one. Our planet has a spheroid form. Although a spheroid resembles a sphere, it differs in radius from the centre to the surface at different points. 
Also read : how to calculate volume of a sphere

Cube and cuboid

The three-dimensional (3D) shapes cube and cuboid share the same number of faces, vertices, and edges. The primary distinction between a cube and a cuboid is that a cube has six square faces, whereas a cuboid has six rectangle faces. The volume and surface area of a cube and a cuboid are different. A cube has the same length, breadth, and height, whereas a cuboid has varied length, width, and height.

Cylinder

A cylinder is a 3D form that has one curved surface, two circular faces—one on top and one on bottom—and two round faces. There is a height and a radius to a cylinder. The perpendicular distance between the top and bottom faces of a cylinder is its height. 

Cone

Another three-dimensional shape is the cone, which has a flat base (of circular shape) and a pointed apex. The cone’s top, pointed end is referred to as the “Apex.” A cone’s surface is also curved. Similar to a cylinder, a cone can be divided into two types: an oblique cone and a right circular cone.

Pyramid

A pyramid is a polyhedron with a flat-faced, straight-edged base and an apex. They can be divided into regular and oblique pyramids depending on how closely their apex aligns with the middle of the base.

• Tetrahedron is the name given to a pyramid having a triangle-shaped base.
• A square pyramid is a pyramid with a quadrilateral foundation.
• Pentagonal pyramids are pyramids with a pentagonal foundation.
• A hexagonal pyramid is one with a base that resembles a standard hexagon.

Prism

Prisms are solids with flat parallelogram sides and identical polygon ends. The following are some traits of a prism: It has a constant cross-section the entire way through.Prisms come in a variety of shapes, including triangles, squares, pentagons, hexagons, and more. Regular prisms and oblique prisms are two other main categories for prisms.

3D images

The three dimensions of a three-dimensional object are length, width, and height/depth. They therefore have features like faces, edges, and vertices. All objects that we can touch are three-dimensional, and three-dimensional figures have an inner and an outside.

3D shape nets

A flattened three-dimensional solid is referred to as a net. Similar to how a two-dimensional outline can be folded and combined to create a three-dimensional image. To generate three-dimensional shapes, nets are utilized. More than one net may be present in a three-dimensional shape.

Their nets are what create 3D objects. A net is produced if we take a cardboard box, cut the edges, and flatten it. We may also do the opposite, enlarging the flattened box and glueing it back together to create a 3D cuboid-shaped object. Architects, civil engineers, and graphic designers all employ 3D drawing.

Items with three dimensions

Only distinguishing characteristics that distinguish 3D objects from 2D objects are the width and depth. 3D objects occupy space and have distinct three dimensions, length, breadth, and width. A Rubik’s cube, a book, a box, a carrot, an ice cream cone, and a barrel with a cylinder shape are examples of 3D items that are all around us.

Solved examples

Example 1:

If the side length of a cube is 6 cm, calculate its volume.

Solution:

Side length, a = 7 cm, as stated.

We are aware that a cube’s volume equals three cubic units.

Consequently, \({7^3} = 7 \times 7 \times 7 = 343c{m^3}\)

Consequently, a cube has a volume of \({216 cm^3}\).

Example 2:

Identify the entire surface area of a sphere with a 3 cm radius. Use (π = 3.14)

Solution:

Radius, r = 3 cm, is provided.

The following is the formula to determine a sphere’s total surface area:

TSA of a sphere equals four \({r^2}\) square units.

TSA of the sphere is \(4 \times 3.14 \times {3^2}c{m^2}\)

Sphere TSA = 113.04  \({cm^2}\)

Consequently, a sphere has a total surface area of 113.04\({cm^2}\).

Example 3:

Find the volume of a cuboid with the following measurements: 4 cm, 6 cm, and 12 cm.

Solution:

The dimensions of a cuboid are 4 cm, 6 cm, and 12 cm.

We are aware that a cuboid has a volume of lbh cubic units.

Thus, the cuboid’s volume is equal to (4)(6)(12) \({cm^3}\)

V = 288 \({cm^3}\)

Consequently, the cuboid has a 288 \({cm^3}\) volume.

Frequently asked questions

1.What three-dimensional shapes are there?

In geometry, three-dimensional shapes are those that have length, breadth, and height as their three determined dimensions.

2.What kinds of three-dimensional shapes are there?

Cone, cylinder, cuboid, cube, sphere, rectangular prism, and pyramid are some examples of the various three-dimensional shapes.

3.Does the square have three dimensions?

The shape of a square is two dimensional rather than three dimensional.

4.What is the name of a round object that is three dimensional?

A sphere is a three-dimensional circular form. A football is a spherical item, for instance.

5.What kinds of forms have three dimensions?

Numerous examples of three-dimensional shapes can be found in the real world, including Rubik’s cubes.

If you need extra assistance with topic, You can checkout Solid Shapes( 3D Shapes, Euler’s Formula) in our Class 8 Math course, where we delve into these concepts in depth. By referring to this lesson, you’ll gain a deeper understanding of the material and boost your exam performance. Join our online Math tuition now for personalized attention, expert guidance, and regular assessments to track your progress. Don’t hesitate – start acing your Math class today!

Introduction

The Ampere is one of the seven fundamental units, which include metre, kilogram, second, Kelvin, mole, and Candela. It is used to measure the flow of electric current and is abbreviated as A or amp. Different systems of units like KGS, CGS, and International SI use different units for current and other basic quantities, and conversions can be made between these units. 

An ammeter is a device that measures electric current in amps flowing through a circuit.

What is Ampere?

Ampere, named after Andre-Marie Ampere, is a unit used to measure electric current. It is abbreviated as amp or A. Ampere was a French physicist and mathematician and is considered the father of electromagnetism. 

Initially, the unit Ampere was defined as an electric current equivalent to the flow of  \({10^{19}}\) elementary charges in 1.602176634 seconds. Later, the unit of charge was defined as the coulomb, and Ampere was defined as the flow of one coulomb of charge per second.

1A = 1 C \({\sec ^{ – 1}}\)

A – Ampere (unit of current)

C – Coulomb (unit of charge)

s – second (unit of time)

In the CGS system, the unit of electric current is the “statampere,” which is approximately equal to 10-10 A, while in the International System of Units (SI), one Ampere is defined as the flow of one coulomb of charge per second.

Prefixes of Ampere

To reduce the number of zeros in numerical equivalences, multiples and submultiples of units can be used. These are commonly expressed using prefixes and we list a few here. 

The most common of these are A, kA, MA, mA, and μA and conversion between these sub units is easy.

Ampere Conversion Table

Conversion of Ampere into milliampere

Conversion of Ampere into microampere

Conversion of Ampere into kiloampere

Conversion of Ampere into Megaampere 

Conversion of Watt, Volt, and Ohm into Ampere 

Conversion of Watt into Ampere 

Unlike Ampere, Watt is a unit of power and we can calculate power from current as follows:

Without knowing voltage or resistance, power cannot be calculated solely from the current. For instance, for a device consuming 3000W of power at 100V, the current is:

Conversion of volt into Ampere 

Once again, Volt is a unit of voltage, not current. We can calculate voltage from current given either the power or the resistance. Here is an example. For a 400W devices operating at 20V, the current is:

Conversion of ohm into Ampere 

Ohm measures resistance and Ohm’s law states that

Ammeter

An ammeter is an electronic device designed to measure the flow of electric current in a circuit, which is usually measured in amperes and thus, the name ammeter is given to them. To measure the current, ammeters are connected in series with the circuit and owing to their low resistance, they do not experience significant voltage while performing the measurement. 

Ammeters are available in different ranges, with some used to measure smaller currents in the milliampere (mA) or even the microampere (μA) range. They can be designed to measure both AC as well as DC current.

Types of Ammeter

Ammeters are classified as below

1. Moving coil ammeter
2. Electrodynamic ammeter
3. Moving iron ammeter
4. Digital ammeter
5. Hotwire ammeter
6. Integration ammeter

1. Moving coil ammeter 

A moving coil ammeter is a type of ammeter that can measure both AC and DC current using magnetic deflection. As implied by the name, the coil in this ammeter rotates freely between permanent magnets, owing to the interaction between the current passing through the coil and the magnetic field across it. The current flowing through the circuit is denoted by a pointer connected to this coil.

2. Electrodynamic ammeter 

This ammeter can also measure AC and DC current with an accuracy of 0.10% to 0.25%. The field produced by a fixed coil is used to rotate another coil here, which can denote the value of current. 

3. Moving iron ammeter 

This type of ammeter can also work on both AC and DC. Here, a specially prepared soft iron moves freely between the poles of a permanent magnet or electromagnet. It can be further classified into repulsion or attraction type.

4. Digital ammeter 

A digital ammeter displays the exact value of the current on a digital display. To measure the current, a shunt resistor is added in series with the circuit, and the voltage across the shunt is calibrated to correspond to the current. The voltage is then converted to a digital signal using an analog-to-digital converter and displayed on the screen.

5. Hot wire ammeter 

The heat produced across the wire causes it to expand, which can measure the value of AC or DC current across the circuit.

Summary

The ampere is the standard SI unit of electric current, and is defined as the flow of electric charge in an electric circuit. An ammeter is an instrument used to measure the flow of current in a circuit, and can measure current in a wide variety of subunits like milliamperes, microamperes, and nanoamperes. Ammeters can work in AC and DC circuits.

Current measured in amperes can be converted into milliamperes, microamperes, and nanoamperes, and one can calculate the power and resistance in circuits given two of the three quantities (voltage, current, resistance). Various types of ammeters, such as moving coil ammeters and digital ammeters, are available to measure current in different scenarios.

 

Frequently Asked Questions

1. What does Ampere denote?

André-Marie Ampère, a French physicist and mathematician, is considered the father of electromagnetism and the unit of current, ampere (amp), was named after him. One ampere is defined as the flow of one coulomb of charge per second.

1A = 1C / 1s

2. List two advantages of digital Ammeters over analog ones.

Given below are two advantages of a digital ammeter.

1. Digital ammeters can even work with a small power supply and their accuracy is very high.
2. They are reliable, economical, and last a longer period of time.

3. Why is the connection of the ammeter necessarily in series? What would happen if we connected it in parallel?

An ammeter is a device that measures the current flowing in a circuit, typically measured in amperes. To accurately measure the current, the ammeter must be connected in series with the circuit components. 

Connecting an ammeter in parallel would result in a drastic increase in current since the resistance is very low, which can generate excess heat and potentially harm the device.

4. Discuss the working of a moving coil ammeter?

A moving coil ammeter is one of the various types of ammeter that can measure both AC and DC current. It uses magnetic deflection, with a coil that rotates freely between permanent magnets. The interaction of magnetic field produced with the magnetic field of the magnets causes a deflection in the coil, which can denote current flow.

5. How to convert a moving coil galvanometer into an ammeter?

A moving coil galvanometer can be converted into an ammeter by connecting a low resistance in parallel with it.

There are two types of shapes: two-dimensional shapes and shapes in flat-plane geometry. They can have any number of sides, and their sides can be either straight or curved. Polygons are plane geometric shapes comprised of lines. Polygons include shapes like triangles and squares. For instance, we can state that 2-D figures are those paper drawings that simply have length and width.

Define Plane

A plane is a two-dimensional surface that can stretch indefinitely in both directions and is measured by two linearly independent locations. In algebra, the points are plotted on a number line that runs continuously and infinitely from left to right, up and down, and in all directions. Two planes can cross each other, be identical to one another, and be in parallel with one another. A plane consists solely of a surface with no depth or width. There are only ever two dimensions. If you imagine a wall and extend it indefinitely, it will turn into a plane.

Plane Figures and Shapes

Squares, rectangles, triangles, circles, pentagons, octagons, hexagons, ovals, and other shapes are examples of plane figures. Circles and ovals are not polygons, but shapes like squares and rectangles that gather together are known as polygons.

A closed two-dimensional or flat surface figure is referred to as a plane shape, as opposed to a solid shape. Instead of having edges and faces, they have a number of thin lines that meet to form a corner or a vertex. Triangles, squares, rectangles, circles, and ovals are some common plane shapes. If we looked closely at a piece of paper, we would see its length and width but not its depth; therefore, since they are created by combining two straight or curved lines, they are closed objects. They are also referred to as polygons or planned geometric shapes.

Examples of Plane Shapes

Squares, rectangles, triangles, circles, pentagons, octagons, hexagons, ovals, etc. are examples of plane shapes.

Triangle: A triangle is a polygon with three sides and three angles.

Quadrilateral: A closed polygon with four sides is referred to as a quadrilateral. Trapezium, Square, Rectangle , rhombus, etc are the examples of quadrilaterals.

Circle: A figure is referred to as a circle if all of its points are equally spaced from a fixed point. The fixed point is referred to as the circle’s center.

Pentagon: A shape is referred to as a pentagon if it has five sides. 

Hexagon: A shape is referred to as a hexagon if it has six sides.

What are Solid Shapes?

What kind of device, a laptop or computer, are you using to read this? Cuboidal! That is correct! Describe a cuboid. It has a strong form. The same applies to cones, cylinders, etc. Solids are shapes that can be observed and measured in three dimensions. Solid shapes are characterized by their length, width, and height, which can also represent thickness or depth. When a two-dimensional object is folded into a three-dimensional shape and put down flat to reveal each face, the result is known as a net pattern. A net is a 3D figure that has been unfolded. Faces, vertices, and edges are the three primary characteristics of solid forms.

Plane Figures and Solid Shapes in your math class? Don’t worry – our online Math tuition can help! We provide comprehensive lessons on these topics, covering everything from basic shapes to more complex geometric figures.

Solid Shapes Examples

Cubes, cuboids, pyramids, prisms, cylinders, spheres, cones, torus, trapezoids, rhombus, parallelograms, and quadrilaterals are a few examples of solid shapes. A pen is made up of two cylinders, and a dome is made up of a hemisphere on a cylinder or a cone. It can also be formed up of two or more actual figures.

Cuboids: Cuboids can be found in everyday objects like bricks, tiffin boxes, books, matchboxes, etc.

Sphere :Globes, marble, oranges, and bubbles are all examples of spheres in everyday life.

Cone: Ice cream cones, traffic cones, party caps, and other objects in everyday life are examples of cones.

Difference between Solid and Plane Figure

Interesting Facts

• When a specific shape is made repeatedly without any gaps or overlapping and covers a plane, the result is a tessellation. Only squares, equilateral triangles, and rectangular hexagons can form regular tessellations.
• Natural tessellation examples include the hexagonal cells in a honeycomb design or the diamond-shaped pattern on a snakeskin.

Solved Examples

1. A cube with a side length of 6 cm has what size surface area?

Ans: The surface area of a cube is \(6{a^2}\).

The area of the surface area is \(6 \times {\left( 6 \right)^2} = 216c{m^2}\)

2. If the radius of a circle is 7 cm, then what is the area of the circle?

Ans: The area of a circle is \(\pi {r^2}\)

The area of a circle is \(\pi {7^2} = \frac{{22}}{7} \times {7^2} = 154c{m^2}\)

Key Features

• Two linearly independent points can be used to measure a plane, which is a two-dimensional surface.
• Squares, rectangles, triangles, circles, pentagons, octagons, hexagons, ovals, and other shapes are examples of plane figures.
• A plane shape is a closed, two-dimensional or flat surface figure.

 

Frequently Asked Questions

1. How has geometry and math gotten so much attention because of the ancient Japanese technique of origami?

Ans: Geometry, mathematics, and engineering have all taken a keen interest in origami, the art of folding paper into three dimensions. It offers a fascinating method for converting a flat plane shape into a solid shape. For instance, methods have been devised for the deployment of airbags in a car and stent implantation from a folded state. A crease pattern can also be folded into a 2D representation. Additionally, it is used to double the cube and trisect an angle.

2. What is Euclidean geometry?

Ans: The study of solid and flat shapes using the axioms and theorems developed by the Greek mathematician Euclid is known as Euclidean geometry (c.300 BCE). The solid and plane geometry is known as euclidean geometry. Angles and circles are two instances of Euclidean geometry. The discipline known as parabolic geometry is based on Euclid’s five postulates. There are two types: solid geometry, which is based on Euclidean geometry in three dimensions, and plane geometry, which is based on Euclidean geometry in two dimensions.

3. What is the point?

In a plane, a point is a dot that has no length, breadth, or height. It establishes a plane’s location. There are two different kinds of points: coplanar and non-coplanar points, as well as collinear and non-collinear points. Non-collinear points do not sit on the same line as collinear points, which are located there. Non-coplanar points do not lie on the same plane as coplanar points, which are parallel to one another.

Introduction

The term “food chemistry” is used to describe the study of the chemical reactions that take place in the preparation and consumption of food. The composition and functional qualities of foods and food products at different stages are the primary areas of study. While food supplies important elements such proteins, carbs, fats, vitamins, lipids, and minerals. The right nutrients should be included in the diet. Plants and animals are both examples of sources that can be used to create food. Because of the biochemical process it triggers in the body, this food is a rich source of fuel. Sugar, a simple type of carbohydrates, is converted into energy during respiration. Response as follows:

Enzymes and preservatives like flavours, food additives, and colours are also found in food. Manufacturers add preservatives and create new food variations to extend the shelf life of these products. Preservatives extend the shelf life of food without adding any nutritional value, similar to how milk is transformed by fermentation or enzymatic action into curd and cheese. Because of this, food science and chemistry have a positive effect on a wide range of aspects, including:

• Techniques for enhancing food’s shelf-life and avoiding the activity of microbes. 
• Methods for food processing and avoiding food deterioration. 
• Most importantly, food safety and quality enhancer methods.

What is Food Chemistry?

It alludes to the chemical composition of the meal and all of the interactions it has with the body and the environment. Chemical composition, how it is altered by cooking, and how it reacts with the human body are all topics covered. Proteins, carbs, and lipids can all be found in their purest forms in biological items like milk, meat, lettuce, poultry, and so on. Hence, food chemistry is concerned with all modifications made to foods and the improvement of their quality through various methods of food processing.

Chemical in Food

What do Food Chemists do?

A good food chemist should know the science behind food and its application. 

1. He should be able to develop improved food and beverages. 
2. He should be able to analyse methods like canning, heat processing, freezing, and packaging. 
3. He must be aware of the effects of processing on the taste, appearance, freshness, aroma, and vitamin and mineral content of food.

Components of Food

The main component is the necessary diet that is required in a large amount by the body. 

Different Chemicals in Food

The other components or chemicals of food help in various functions of the body and their small quantities are enough.

Other chemicals listed below as preservatives added to food are unhealthy.

Food Components Can Be Broadly Differentiated Into Two Categories.

The food components are divided into two categories: Macronutrients and Micronutrients.

Summary

To learn about the science behind the components of food and their qualities, one must study food chemistry, a large field. It goes through every conceivable structural and molecular shift. A food chemist can oversee these modifications to ensure they don’t compromise the food’s safety or nutritional value in any way. In order for the body to develop and function normally, it need a diet that is both varied and complete.

Frequently Asked Questions

1. Why are preservatives bad for food?

Ans: Some chemicals (present in preservatives) can cause toxic effects like kidney damage, liver disease, DNA damage or impairment of the nervous system, and gastrointestinal symptoms. 

2. What is an alternative for no chemical food?

Ans: Organic food is an alternative, since it has no chemicals  like pesticides or artificial fertilisers. 

3. Why does organic foods spoil faster?

Ans: Organic food is healthy as they are not treated with preservatives or waxes. Therefore, due to the absence of chemicals or preservatives, the shelf life of food decreases and spoils the food at a faster rate. 

Introduction

What happens to a food’s composition, chemistry, and physics while it’s prepared for storage and later consumed is the focus of food chemistry. Recent decades have seen significant expansion in the field of food chemistry. The science of food chemistry investigates the chemical and physical changes that occur in food over time.

The study of compounds used for food preservation through additives is also a part of this field of study. Maleic acid was initially extracted from apples by scientist Carl Wilhelm Scheele in the early 17th century. Then, for ages, scientists have explored food chemistry, searching for new additives and preservatives to boost food quality.

What is Food Chemistry?

The study of foods and their non-living and living constituents is the focus of food chemistry, a scientific discipline in the field of food science. Carbohydrates, lipids, proteins, flavouring compounds, food additives, etc. are all areas where it crosses with biochemistry.

In addition to fats, proteins, and carbs, water is a crucial aspect of every balanced diet.

It discusses the components of food in terms of their content, structure, and physical and chemical qualities. 

In 1950, numerous scientists sought to uncover the root of food additives to combat food contamination. Chemical and physical thermodynamics, quantum mechanics, biopolymer science, colloidal interaction, etc. all contribute to the overarching concept of food chemistry.

Examples of Food Chemistry

Food chemistry is seen in day to day life. Some of the examples are:

• The fermentation of milk, or the creation of curd, and the use of lemon juice to keep apples from browning provide useful analogies.
• In order to determine whether or not a food is safe to eat, food chemists analyse its chemical components. It extends the shelf life of food and is utilised in the preservation process.
• Natural chemicals and enzymes are employed extensively in the food industry to create novel products, such as yeast’s application in baking and lactobacillus’ application in the production of curd from milk.
• Sodium nitrate and vinegar (acetic acid) are just two of the many substances found to extend the shelf life of pickles and other foods.
• Preservatives and other food additives are used to extend the shelf life of fruit juices.

Components of Food

Water is the primary component of most of the foods we eat, however the amount varies widely. Carbohydrates, fats, and proteins are also important parts of a balanced diet. Minerals, vitamins, enzymes, etc., are examples of foods’ ancillary components.

Water: 

Depending on the cuisine, the amount of water in it might range between 40-95%. In the processes of emulsification, freezing, baking, and gel formation, water plays a critical role.

Proteins: 

Amino acids form complicated proteins. These amino acids rebuild bones, muscles, and skin. 50% of a live cell weighs these. It’s required for body growth, hence food contains it. Legumes, grains, beans, peanuts, meat, fish, milk products, and soya milk contain it. Carbon, hydrogen, nitrogen, and oxygen comprise a protein molecule. Food sources provide eight important amino acids. Leucine, valine, tryptophan, tyrosine, lysine, methionine, isoleucine, and phenylalanine.

Carbohydrate: 

Carbohydrates are organic compounds found in many food components like sugar, starch, dextrins, Celluloses, pectins, etc. These are the main source of energy. The carbohydrates are of three types:

1. Monosaccharides,: Glucose, Fructose
2. Disaccharides: Sucrose
3. Polysaccharides: Starch, Glycogen, Cellulose, etc, 

Lipids: 

Food contains oils, fatty acids, and steroids from grains, animal fats, milk products, soybeans, meat, waxes, etc. These are water-insoluble, non-polar dietary compounds that boost energy. Cell membranes need it to store energy.

Vitamins: 

Vitamins are required in a very small amount in our body. These are essential for various metabolic activities of the body. Examples of vitamins are: 

1. Water-Soluble: Vitamin-B (Thiamine, Riboflavin, Niacin, Biotin, Pantothenic Acid, Folic Acid), and Vitamin-C (Ascorbic acid).
2. Fat-Soluble: Vitamin-A, Vitamin-D, Vitamin-E, And Vitamin-K.

Minerals: 

Minerals are also crucial to our health and are found in many different foods. Excessive use can be harmful to health, thus only a modest amount is needed. Calcium, magnesium, potassium, copper, iron, and zinc are all examples of minerals that play an important role in human health.

Structure 

Let’s understand food components by their structure.

Carbohydrates: A single carbohydrate molecule is calles a monosaccharide, while two or more carbohydrate molecules are called disaccharide and polysaccharide. 

Carbohydrates

Proteins: Proteins are the chain of amino acids bonded by the peptide bond between the amino group and the carboxylic group. 

Lipids: Lipids are of two types saturated and unsaturated fatty acids. Triglycerides are formed by one molecule of glycerol and three molecules of fatty acids. In the reaction, the R, R’, R” are the chains of 10 to 20 carbon. 

Summary 

Food chemistry is the study of the chemical and physical modifications made to foods and their constituents. Additives, preservatives, flavouring agents, enzymes, minerals, and vitamins are now included included in the field of food science. Carbohydrates make up a sizable portion of the food we eat.

Some of the most important vitamins for our bodies are carried by lipids, which are present in oil cereals, meat, milk, and dairy products.

Frequently Asked Questions 

1. How is a mixture of oil and water stabilized in food chemistry?

Ans. Emulsifiers are the chemical components used for mixing two food containing oil and water. One of the natural emulsifiers is Lecithin found in egg yolk and plant tissues which are used to make mayonnaise and salad dressings. 

2. What is the importance of phosphorus?

Ans. Phosphorus is an important macro mineral in our body, it is found in many foods like fats from animal meat, fish, egg, and milk. It is important for DNA and RNa production.

3. What is aromatic food?

Ans. Aromatics are vegetables, herbs, and spices that add aroma and flavor to dishes. They consist of mainly phenols.

Introduction

Mankind has only recently begun to utilise fluorine. Materials containing fluorine were infrequently used in antiquity. Smelting fluorite was an economic focus for Georgius Agricola, who investigated its application in the 16th century. Both the word “fluorite” and “fluorine” were created by Agricola. In the later part of the 18th century, hydrofluoric acid was uncovered. Much like chlorine, fluorine was discovered to be bound in compounds in the nineteenth century. Calcium fluoride, or fluorite, is a mineral that can be discovered. Fluorine is difficult to separate because of its strong bonds and the toxicity of hydrogen fluoride. Electrolysis of potassium fluoride and hydrogen fluoride produced elemental fluorine in 1886, and the discovery was made by French chemist and Nobel laureate Henri Moissan. During World War 2, massive amounts of fluorine were produced and utilised by the Manhattan Project. Polytetrafluoroethylene (Teflon) plastic and refrigerant gases were both developed by DuPont this century (Freon).

What is Fluorine?

Gaseous halogen the element fluorine can be found in the 17th group of the periodic chart. The element has an atomic number of 9. One of fluorine’s defining characteristics is that it is the most electronegative element in the periodic table. Under normal conditions, it presents as a pale yellow diatomic gas that is highly toxic. At 3.98 on the Pauling scale, fluorine has the highest electronegativity of any element.

Electron Configuration And Chemical Properties of Fluorine

The gas fluorine, which belongs to the 17th group, has an atomic number of 9. The halogen nature of fluorine gives it a valency of one. Due to its one electron deficit, it accepts electrons from other substances. They accept electrons, making these compounds oxidising agents. Don’t forget that electron donors always act as reducing agents and electron acceptors as oxidising ones. Because of its high electronegativity, fluorine is the most powerful oxidising agent among the halogens. An electrical configuration of 1s22s22p5 describes fluorine.

Fluorine 

Properties of Fluorine

Fluorine shows different physical and chemical properties. 

Chemical Properties of Fluorine

• Fluorine is one of the most powerful oxidising agents since it is a strongly electronegative element. According to the Pauling scale, fluorine has an electronegativity of 3.98.
•  The strong force of attraction between the nucleus and the electrons caused by their small size results in a very high energy requirement to extract an electron. Fluorine has an initial ionisation energy of 1680.6 KJ/Mol. Thus, it takes 1680.6 KJ of energy to remove an electron from a mole of fluorine. 
• Fluorine has a standard potential of 2.87 V. Compared to all other factors, this is the highest. 
• There is only one stable isotope of fluorine, which is fluorine 19.

Physical properties of Fluorine

• Fluorine is the lightest of all the halogens, with an estimated atomic mass of 19 particles. 
• In its natural state, fluorine can be found as a gas. It is a light gas with a pale-yellow colour. 
• Fluorine has a boiling point of -188° C and a melting point of 219.6° C.

The Atomic Radius of Fluorine

The atomic radius of fluorine, a very small element, is extremely small. A fluorine atom has a very strong nuclear force because of this. The smallest halogen atom is fluorine, which has an atomic radius of only 147 pm.

What is the Atomic Mass of Fluorine?

The lightest halogen gas, fluorine, weighs only 19 amu; specifically, it is 18.99 amu. Conventionally, we round it off and count it as 19.

Fun Facts About Fluorine

• In the crust of the earth, fluorine is the 13th most abundant element.
• Fluorine is a very reactive element that is never discovered in its pure form. It is always present in some combination with another element.
• Water can be burned by fluorine with a brilliant blaze.
• Fluorine can also be found in the earth’s crust in addition to the air. Coal and other elements contain fluorine in trace amounts. 
• Fluorine is nearly non-existent in the air. 50 parts per billion roughly. Before the Second World War, fluorine was not well recognised in the business.
• Fluorine hadn’t been produced commercially until that point. Everyone just understood fluorine as an element that can combine to form salts. Uranium hexafluoride, however, was discovered to have nuclear capabilities and be a source of energy during World War 2. Fluorine has since been produced industrially at an exponential rate. 
• Animals require ion fluoride, which helps to strengthen their teeth and bones. In some places, it is added to drinking water. 

Summary

Fluorine is one of the halogen family members in the periodic table. Fluorine exists as yellow gas having an unpleasant smell when it is at room temperature. It is harmful to breathe in the gas. Fluorine becomes a yellow liquid when it cools. Fluorine-19 is the only stable isotope of the substance. The most significant source of fluorine is fluorspar.

 

Frequently Asked Questions

1. What are the principle sources of Fluorine?

Ans: The principal source mineral, fluorite, was originally reported in 1529 by Georgius Agricola, known as the “father of mineralogy,” and the word “fluorine” is derived from this Latin stem. Fluorite, according to him, is an addition known as a flux that aids in melting ores and slags during smelting.

2. Why is Fluorine so important?

Ans: Our bones’ ability to remain firm depends on fluorine. If we use fluoridated toothpaste twice a day, it can also prevent tooth decay. Too much fluorine absorption can affect the kidneys, bones, nerves, and muscles in addition to causing osteoporosis and tooth decay.

3. What are the safety precautions for handling fluorine?

Ans: Use and store fluorine in a ventilated gas cabinet or fume hood. When a gas cabinet is warranted (e.g., cylinders larger than lecture bottle size that are used in a fume hood), install a fluorine gas monitoring system. Follow all applicable recommendations for storage and handling of compressed gases.

Introduction

The chemical symbol for flerovium is Fl, and the atomic number of flerovium is 114. Super heavy describes this element’s status as one of the heaviest in the periodic table.

It’s also a highly radioactive substance or component. It wasn’t until 1998, in a Russian research facility, that this element was found.

The p-block is represented by elements in the periodic table by those in group 14, period 7. In its electronic form, flerovium has the formula\(\left[ {{\bf{Rn}}} \right]{\rm{ }}{\bf{5}}{{\bf{f}}^{14}}{\bf{6}}{{\bf{d}}^{10}}{\bf{7}}{{\bf{s}}^2}{\bf{7}}{{\bf{p}}^2}\). Since it is the most massive element in the carbon (C) family, it is a member of that family. Its radioactivity means that only a little amount of this element may ever be produced.

What is Flerovium?

With an atomic number of 114 and the symbol, flerovium is one of the heaviest known elements (Fl). To be specific, this element belongs to the p-block. It is part of period 7 and the 14th group. Then it must be one of the elements of the carbon group. It’s also the heaviest member of the carbon family. As a man-made substance, it is also highly (very) radioactive (does not occur naturally on the surface of the earth).

At the time of its discovery in 1998, the element was given the name flerovium in honour of the flerov laboratory of nuclear reactions in Dubna, Russia (Asia). However, over time, the name was changed to the flerov to honour the Russian physicist Georgy Flyorov. According to estimates, its mass will be 289.

How Scientists Discovered Flerovium Elements?

In 1998, researchers at Russia’s Joint Institute for Nuclear Research in Dubna successfully synthesised flerovium. They pounded plutonium atoms with calcium ions.

One atom of flerovium-289, an isotope with a half-life of around 21 seconds, was created in this process.

What are the Uses of Flerovium?

Due to it being the heaviest element and the radioactive, Flerovium has very few applications. This substance has zero practical applications outside of academic institutions. No biological function is served by it Its formation in nuclear reactors is possible. Very few flerovium atoms have been created or identified so far. Because of its hazardous properties, it is also not used in commercial applications (as it is a radioactive element).

Flerovium Chemical Properties

• Flerovium is the bulky member present in group 14 elements found below lead.
• The chemical behaviour of the element is expected to be very distinctive.
• The 7s orbitals (s, p, d, f…) are very (largely) highly (more) stabilized (stable) in flerovium, therefore a very large \(s{p^3}\) (type) orbital (orbits) hybridization is needed to achieve a +4-oxidation state (O.S.).
• Flerovium is predicted to be more stable (most) than lead (Pb) in its +2-oxidation state while at a +4 (O.S.)-oxidation state it should be highly (very much) unstable.

Physical Properties of Flerovium

Some of the physical properties of Flerovium element are as follows-

• Appearance- Liquid phase at STP (predicted)
• Melting Point (M.P.)- It has a melting point of around 200K or -73 °C or -100 °F.
• Boiling Point (B.P.)- It has a boiling point of around 380K or 107 °C or 224°F.
• Density- It has a density of approximately 9.928 \(g/c{m^3}\).
• Crystal Structure- Flerovium has a face-centred cubic lattice type.

General Properties of The Fl Element

Flerovium is a rarely used heavy material. Its atomic number is 114 and the molar mass is predicted to be 289. It is denoted or represented by the symbol Fl. It is a carbon group element that lies in the p-block of the periodic table. Its colour is predicted (assumed) to be silvery-white, grey, or metallic. Sometimes it is also known as Ununquadio. Flerovium is a radioactive synthetic element with five known isotopes so far. 

Fun Facts About the Fl Element 

• Flerovium is considered a metal due to its high density and it is an extremely radioactive metal.
• This metal or element can be rarely produced in nuclear reactors.
• Its production is very expensive.
• It is obtained by bombarding plutonium ions and calcium.
• It is a p-block element present in the carbon group.

Summary

Flerovium represented or denoted by the symbol (Fl) is one of the heaviest known elements with the atomic number (Z) 114. It is a p-block element. It lies in group 14 and period 7. That means it is a carbon group element. And it is the heavier element in the carbon group and the p-block. It is also an extremely (very much) radioactive man-made element (does not occur naturally on the surface of the earth). At the time of discovery, it was named after (the place where it was produced) flerov laboratory (lab) of nuclear reactions located in Dubna, a place in Russia, where this element (metal) was produced (discovered) in the year 1998. Element is produced by bombarding a target (aim) of plutonium-244 (\(Pu_{94}^{244}\)) with the nuclei (accelerated) of calcium (\(Ca_{20}^{48}\)):

 

Frequently Asked Questions

1. How many isotopes of Flerovium are known?

Ans: Flerovium has seven known isotopes, and possibly 2 nuclear isomers. The longest-lived isotope is \({}^{289}Fl\) with a half-life of 1.9 seconds, but the unconfirmed \({}^{290}Fl\) may have a longer half-life of 19 seconds.

2. Who discovered flerovium and when?

Ans: A team of scientists from JINR (Joint Institute for Nuclear Research), located in Dubna, a place in Russia discovered the flerovium (element) in the year 1998.

3. Write the reaction involved in the formation of flerovium.

Ans: The reaction involved in the formation of flerovium is –