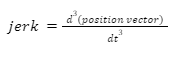Introduction
Acceleration is a physical quantity that describes change in velocity over a given time interval. It is a vector quantity with both magnitude and direction, and is measured in metres per second squared (\(m/{s^2}\)). Acceleration can be thought of as the derivative of velocity or the second derivative of position.
An object moving at a constant velocity has zero acceleration. Thus, acceleration occurs when an object changes its speed or direction, and it is a measure of an object’s ability to reach a given speed.
There are two types of acceleration: average and instantaneous. Graphs, such as velocity-time, position-time, and acceleration-time graphs, can be used to mathematically represent the motion of an object and develop a better understanding of its motion.
What is the Acceleration-Time Graph?
The acceleration-time graph is a pictorial representation of an object’s motion wherein, time is taken on the X-axis as the primary variable, and acceleration is represented on the Y-axis as a function of time.
The area of this graph gives velocity, whereas its slope leads us to a physical quantity that is known as jerk.
Acceleration-Time Graph Explanation
Since the acceleration in such graphs is shown as a function of time, they can be used to understand how an object’s acceleration varies over time. If the graph is going down with time, it means the object is losing acceleration.
When an object undergoes negative or reverse acceleration, it is said to experience retardation.
Special cases in acceleration-time graph
- When particle moving with constant acceleration: If the acceleration of a particle is a constant given by at time , which does not change with time, it will be represented by a horizontal line in the graph.
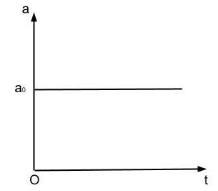
Uniform acceleration
- When a particle is moving with increasing acceleration at constant rate: Acceleration that is increasing at a constant rate will be shown by a straight line making an acute angle with the x-axis or the horizontal.
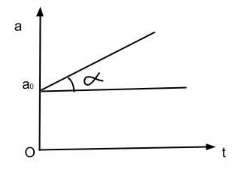
Increasing acceleration
- When a particle is moving with decreasing acceleration at constant rate: If the acceleration is decreasing at a constant rate, it is bound to reach zero after a given time interval. Thus, such a graph is a straight line making an obtuse angle with the x-axis.
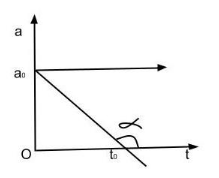
Decreasing acceleration
Vertical Axis
The acceleration of an object is displayed on the Y-axis of a graph, with time on the X-axis. This allows us to see how acceleration changes with respect to time.
Acceleration-time graph
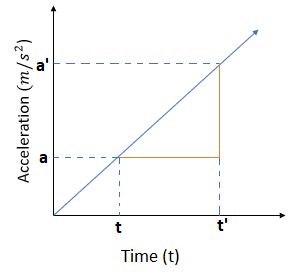
Slope of the Acceleration Graph
Given a graph, we can calculate its slope, which would allow us to measure its steepness. For an acceleration-time graph, the slope represents the change in acceleration over time, which is known as jerk. In mathematical terms, it is the third derivative of the position vector. The sensation of jerk is experienced when there is a change in acceleration with respect to time.
\(\begin{array}{l}Slope = \frac{{\Delta y}}{{\Delta x}}\\jerk = \frac{{Change\;in\;acceleration}}{{change\;in\;time}}\end{array}\)
Acceleration-time graph
Jerk: Jerk is the rate of change of acceleration. The derived unit of jerk is
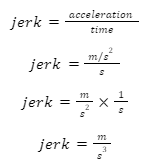
Thus, its unit is \(m/{s^3}\).
The dimension of jerk:
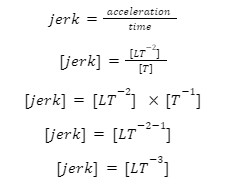
Example of jerk: Suppose a car is in motion with a given acceleration and the driver suddenly notices a speed bump. He will slow down rapidly and thus, the car’s acceleration changes abruptly in a short period of time. This sudden change in acceleration creates a jerky motion for objects inside the car, which is an example of jerk in action.
Area Under the Acceleration Graph
When we calculate the area under an acceleration-time graph, we arrive at the object’s velocity. This is easy to prove since area of a curve is given by xy.
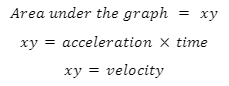
Velocity: Velocity represents the time rate of change of an object’s displacement.
\(Velocity = \frac{{displacement}}{{time}}\)
Its SI unit is and dimension is \(\left[ {L{T^{ – 1}}} \right]\).
Important Things To Remember In Acceleration Time Graph
- The slope of an acceleration-time graph gives us jerk.
- Two objects have coinciding acceleration-time curves when their accelerations are the same.
- Motion with constant acceleration would yield a straight line curve with zero slope, i.e., the line would be horizontal.
Acceleration Graph Solved Example
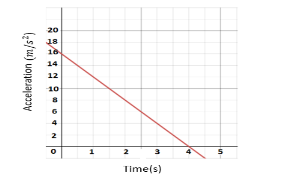
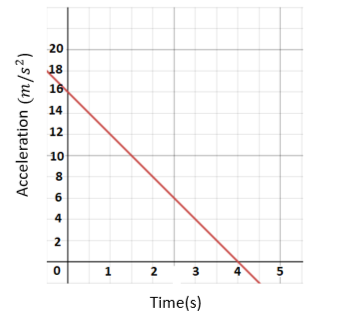
Example 1: Using the given graph, find velocity.
Acceleration-time graph
Solution: We can see that in the curve,
\(\begin{array}{l}a = m/{s^2}\\t = 4s\end{array}\)
Area under the curve will give us the velocity of the object.
\(\begin{array}{l}Velocity = acceleration \times time\\v = 15m/{s^2} \times 4s\\v = 60m/s\end{array}\)
Hence the velocity of the object is .
Example 2: If the acceleration of a car is given as ![]() , find the jerk at time .
, find the jerk at time .
Solution: We are given that
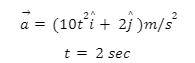
Since jerk is the first order derivative of acceleration. Thus,
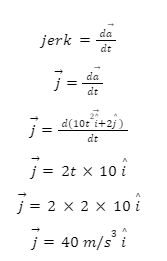
Therefore, the jerk experienced the car is 40 \(m/{s^3}\) in the x-direction.
Summary
In a graph showing the variation of acceleration with time, time is represented on the x-axis and acceleration on the y-axis. This is because time is a primary and independent quantity whereas acceleration depends on time.
The slope of the acceleration-time graph represents the rate of change of acceleration, commonly known as jerk. Jerk is felt by the body when there is a sudden change in acceleration with respect to time and can be calculated as the third order derivative of the position vector. Just like acceleration, jerk is a vector quantity with both magnitude and direction.
Frequently Asked Questions
1.How can we find the jerk from the acceleration-time graph?
Jerk is the slope of the acceleration-time graph and can be calculated thus.
2. How can we find velocity from the acceleration-time graph?
If we wish to find velocity, all we need to do is calculate the area under the curve.
3. What is the use of an acceleration-time graph?
The graph helps us pictorially represent an object’s motion and calculate associated quantities of motion.
4. What is the relation between jerk and position vector?
Jerk is the third order derivative of the position vector.