Introduction
When an electric current flows through a straight copper wire, it generates a magnetic field that forms circular patterns around the wire. The Biot-Savart law is a relation that allows us to calculate the strength of this magnetic field at different distances from the wire. And its applications aren’t limited to straight wires. For instance, when current flows through a circular loop of wire, a magnetic field forms along the axis of the loop and by analyzing small segments of the wire, we can again use Biot-Savart law to understand this magnetic field. Thus, the Biot-Savart law helps us derive magnetic fields due to current-carrying conductors.

Magnetic field due to wire
What is Biot-Savart Law?
A rod with an electrical coil carrying current wound around it can act as a magnet. Similarly, when current passes through a straight electrical wire, it creates a magnetic field. Although the measurement methods for an electrical coil and straight electrical wire differ slightly, the principle remains the same – magnetic fields originate around a conductor carrying an electric current. Through experiments with electric current and conducting wires of various shapes, the properties and characteristics of magnetic fields were understood, leading to the development of the Biot-Savart Law. Further, the direction of the magnetic field can be arrived at using the following two rules:
- The right-hand rule
- The right-hand thumb rule
The first of these rules is related to the force experienced by charged particles in a magnetic field while the latter is related to Biot-Savart law. The latter being our focus, we state it here. According to the right hand thumb rule, if we point our thumb along the direction of current flow, our fingers curl around in the direction of the magnetic field.
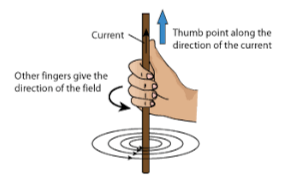
Derivation of Biot-Savart Law
According to the Biot-Savart law, the magnetic field created by an infitesimal current element dl carrying a current I at a point P is:
- Directly proportional to the current and the length of the element (I dl).
- Directly proportional to the sine of angle made by the direction of current and the length of the element.
- Inversely proportional to the square of the distance from the element to the point in question.
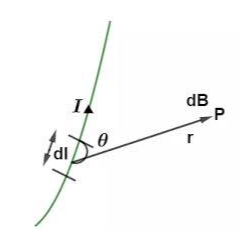
Biot-Savart law

Biot-Savart Law Formula
A general formula that can be derived via the Biot-Savart law is that of a magnetic field created by a coil of N turns along its axis. It is given as:
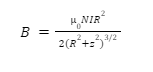
Here,
N = Number of turns in the coil
I = Current flowing through the coil
R = Radius of the coil
z = Distance along the axis to the point where the magnetic field is being calculated.
At the centre of the coil, z=0 and the formula becomes:

Applications of Biot-Savart’s Law
Since Biot-Savart law can estimate magnetic fields, it can be used to estimate the sag that high tension lines would undergo and prevent them from snapping.
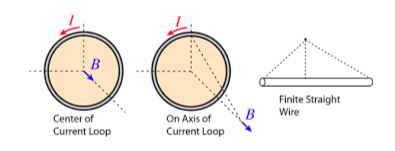
Biot-Savart law also enables us to determine the strength of the magnetic field at the centre of a current loop or at any point on its axis, as well as at a distance from a straight current-carrying wire. These scenarios are depicted in the figure above. Further, we can apply this law in aerodynamics theory to calculate and understand the characteristics of a vortex produced by high-velocity air pressure, which is shown in the figure below. Finally, we can employ it to model the atomic responses inside magnetic fields.
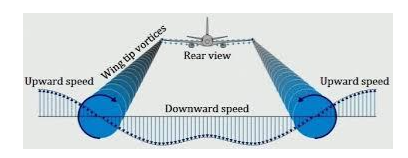
Vortex of air
Importance of Biot-Savart’s Law
The various applications of this law have already been demonstrated. Thus, it comes in of immense use in almost all fields of physics and engineering. Here are a few examples:
Example: What is the magnetic field at the centre “O” in the figure shown below?
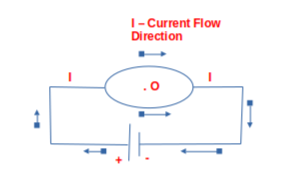
Since the current on either portion of the circle is in the same directions, the magnetic fields point in the opposite direction (use right hand thumb rule). Thus, they cancel out and we have
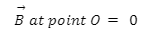
Summary
Biot-Savart law is a fundamental law in magnetostatics that explains the relationship between currents and magnetic fields. It is applicable in the case of static currents and plays a significant role in calculating the velocity of vortex lines in aerodynamics. This law is consistent with Gauss’ and Ampere’s laws and its applications include determining the field due to current on a conductor or a current-carrying loop.
Frequently Asked Questions
1. What is the other name of Biot-Savart law?
The Biot-Savart law is also known as Laplace’s law.
2. What is the value of relative permeability in the air?
Air has a relative permeability of 1.
3. Describe Helmholtz coils and their application.
Helmholtz coils are two identical coils placed a certain distance apart with their axes coinciding. When current flows through them, a region of almost uniform magnetic field is obtained between them.
4. What is the unit of permeability as a unit of force?
In units of force, the unit of permeability is \(N{A^{ – 2}}\).
5. What is the flux density at the center of a solenoid coil with lengths L and N turns?
At the centre of a solenoid, magnetic flux density is given as \(\overrightarrow B = \frac{{{\mu _0}NI}}{L}\).