Introduction
The volume of a pyramid is the space engulfed between the faces of the pyramid. The volume of the pyramid depends on the area of the base of the pyramid and the height of the pyramid. The different types of the pyramid consist of different bases so the volume of the pyramid differs from each other as the areas of the bases are different because a triangular pyramid has a triangle base and a square pyramid has a square base, the base areas are different so, the volume of the pyramid also different.
What is a Pyramid?
A pyramid is a three-dimensional solid structure with a polygon base and the other faces as triangles with all the vertex of the base linked to a single point called the apex of the pyramid. All the triangle faces are lateral faces. There are many types of pyramids each differing by the different-sided polygon base. If the base of the pyramid has n-sides then the pyramid has n+1 faces, n+1 vertices, and 2n edges. The perpendicular distance from the apex to the base is called the height of the pyramid, the perpendicular distance from the apex to any edge of the base is called the slant height of the pyramid.
Example: The pyramids of Egypt, etc.
Types of pyramids
The polygon bases make the pyramids differ from each other. Each type of pyramid has a different polygon base.
Triangular Pyramid: If the base of the pyramid is a triangle then the pyramid is called a triangular pyramid. A triangular base is a three-sided polygon.
Number of faces of the pyramid (n=3) : 3 + 1 = 4
Number of vertices of the pyramid (n=3) : 3 + 1 = 4
Number of edges of the pyramid (n=3) : 23 = 6
Square Pyramid: If the base of the pyramid is a square then the pyramid is called a square pyramid. A square base is a four-sided polygon. All sides of the base are equal in length.
Number of faces of the pyramid (n=4) : 4 + 1 = 5
Number of vertices of the pyramid (n=4) : 4 + 1 = 5
Number of edges of the pyramid (n=4) : \(2 \times 4 = 8\)
Rectangular Pyramid: If the base of the pyramid is a rectangle then the pyramid is called a rectangular pyramid. A rectangular base is a four-sided polygon. All the opposite sides of the base are equal in length.
Number of faces of the pyramid (n=4) : 4 + 1 = 5
Number of vertices of the pyramid (n=4) : 4 + 1 = 5
Number of edges of the pyramid (n=4) : \(2 \times 4 = 8\)
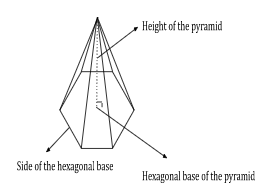
Hexagonal Pyramid: If the base of the pyramid is a hexagon then the pyramid is called a hexagonal pyramid. A hexagon base is a six-sided polygon.
Number of faces of the pyramid (n=6) : 6 + 1 = 7
Number of vertices of the pyramid (n=6) : 6 + 1 = 7
Number of edges of the pyramid (n=4) : \(2 \times 6 = 12\)
There are other types of pyramids like a pentagonal pyramid with a five-sided pentagon as the base, etc…
These pyramids also differ as regular and irregular pyramids based on the base, if the base of the pyramid is regular then it is a regular pyramid. If the base of the pyramid is irregular then it is an irregular pyramid.
Don’t miss the chance to master the concept of ‘Volume of a Pyramid’. Join our Maths Tuition now and unlock your full potential!
What is the volume of a Pyramid?
The volume of a pyramid depends upon the base area and the height of the pyramid (the perpendicular distance from the apex point to the base of the pyramid).
Consider the area of the base of the pyramid as B.
The height of the pyramid is H.
The formula for the volume of the pyramid:
The volume of the pyramid = \(\frac{1}{3} \times B \times H\)
Units of the volume of the pyramid would be cubic units. Also should convert all the parameter units into one unit before calculating the volume of the pyramid.
As we know there are different types of pyramids based on different bases (different bases contain different base areas) let’s check the volume of the pyramid for the different types of the pyramid.
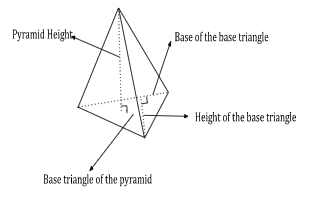
Triangular Pyramid: We know that a triangular pyramid contains a triangle base. The volume of a triangular pyramid would be:
Consider H as the height of the pyramid, h as the height of the base triangle for the base that has length b:
The area of the base triangle would be B= \(\frac{1}{2} \times b \times h\)
Substituting B in the volume of the pyramid formula:
The volume of the triangular pyramid =\( = \frac{1}{3} \times B \times H = \frac{1}{3} \times \frac{1}{2} \times b \times h \times H\)
The volume of the triangular pyramid =\(\frac{1}{6} \times b \times h \times H\)
Square Pyramid: We know that a square pyramid contains a square base. The volume of a square pyramid would be:
Consider H as the height of the pyramid, and a as the length of the side of the square:
The area of the base square would be B=\({a^2}\)
Substituting B in the volume of the pyramid formula:
The volume of the square pyramid\( = \frac{1}{3} \times B \times H = \frac{1}{3} \times {a^2} \times H\)
The volume of the square pyramid\( = \frac{1}{3} \times {a^2} \times H\)

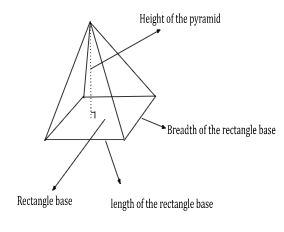
Rectangular pyramid: We know that a rectangular pyramid contains a rectangle base. The volume of a rectangular pyramid would be:
Consider H as the height of the pyramid, l as the length of the rectangle base, and b as the breadth of the rectangle base,
The area of the base rectangle would be \(B = l \times b\)
Substituting B in the volume of the pyramid formula:
The volume of the rectangular pyramid\( = \frac{1}{3} \times B \times H = \frac{1}{3} \times l \times b \times h\)
The volume of the rectangular pyramid\( = \frac{1}{3} \times l \times b \times h\)
Hexagonal (regular) Pyramid: We know that a hexagonal pyramid contains a hexagon base. Considering this is a regular hexagon all the side lengths of the hexagon would be the same. The volume of a hexagonal pyramid would be:
Consider H as the height of the pyramid, and a as the length of the side of the hexagon
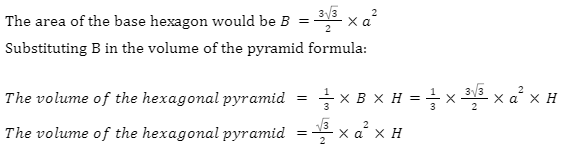
Solved Examples
1. A square pyramid has a height of 10cm and the length of the side of the square base is 3cm. Find the volume of the square pyramid?
Given the height of the pyramid H = 10cm,
The length of the side of the square base a = 3cm
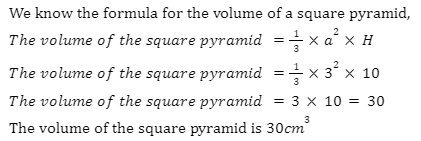
2. A rectangular pyramid has a height of 15cm, the length of the rectangular base is 5cm, and the breadth of the rectangular base is 4cm. Find the volume of the rectangular pyramid?

Word Problems
1. Consider an Egyptian pyramid with a square base of 50m side length and height of the pyramid is 150m, Find the volume of the Egyptian pyramid?
Given the height of the pyramid H = 150m,
The length of the side of the square base a = 50m
Summary
A pyramid is a polyhedron as the faces of a pyramid is made up of different polygons. The volume of a pyramid is the space occupied by the pyramid in the three-dimensional space. In this tutorial, we learned about pyramids, different types of pyramids, the volume of a pyramid, the volume of different types of pyramids, how to calculate the volume of the different types of a pyramid, and a few examples .
Frequently Asked Questions
1. What is the volume of a triangular pyramid?
The volume of the triangular pyramid = \(\frac{1}{6} \times b \times h \times H\)
H is the height of the pyramid, b and h are the base and height of the base triangle.
2. What is meant by an irregular hexagonal pyramid?
An irregular hexagonal pyramid has an irregular hexagon (all side lengths are not equal) as the base of the pyramid.
3. What is meant by slant height in a pyramid?
The perpendicular distance from the apex to any edge of the base is called the slant height of the pyramid.
4. What is the volume of a regular hexagonal pyramid?
The volume of the hexagonal pyramid\( = \frac{{\sqrt 3 }}{2} \times {a^2} \times H\)
H is the height of the pyramid, a is the side length of the hexagonal base.
5. What is the volume of a rectangular pyramid?
The volume of the rectangular pyramid\( = \frac{1}{3} \times l \times b \times h\)
H is the height of the pyramid, l and b are the length and breadth of the base rectangle.
Also Read : Volume of Cuboid
Volume Of Sphere
