Introduction
In every area of our lives, we are surrounded by numbers. Factors and multiples are also commonly used in our daily life. We use factors when we want to arrange things differently. For example, arrange books in rows and columns, group children in different ways, etc. Let’s consider the number 112. 112 can be divided by 1, 2, 4, 7, 8, 14, 16, 28, 56, and 112. So the factors of 112 are 1, 2, 4, 8, 14, 16, 28, 56 and 112. Likewise, the factors of 112 are -1, -2, -4, -8, -14, -16, -28, -56, and -112. Therefore, when looking for or solving problems involving factors, only positive numbers, negative numbers, whole numbers, and non-decimal numbers are considered.
Properties of factors
- All integers have a finite number of factors.
- The factor of a number is always less than or equal to the number; it can never be greater than the number.
- Except 0 and 1, every integer has at least two factors: 1 and the number itself.
- Find factors by using division and multiplication.
Prime factorization
When we write a number as the product of all its prime factors, it is called prime factorization. Every number in prime factorization is prime. To write a number as the product of prime factors, we may sometimes have to repeat these factors as well.
Example: To write the prime factorization of 8, we can write
\(8{\rm{ }} = \;2 \times 2 \times 2\)
that is, the prime factor 2 repeated 3 times. To write the prime factorization of 112, we can write
\(112 = 2 \times 2 \times 2 \times 2 \times 7\),
which is the prime factor of 2 repeated four times and multiplied by 7.
Therefore, the prime factors of 112 are 2 and 7. A number with more than two factors is called a composite number.
The number 112 has more than two factors.
Therefore, 112 is a composite number.
we know,
A number that is not divisible by any other number is called a prime number.
In the factors of 112, we get that
\({2^4}{\rm{ \times }}7\) is prime.
Steps to find factors of 112
- First we divide the given number 112 by to get a remainder of 0.
- After getting the answer, all the numbers we get are called factors of the given number.
- 1 is the only number that has factors of all numbers.
- The given number itself is the highest factor of the given number.
What are the factors of 112?
We use LCM to find the prime factorization of 112.
Prime factors of \(112{\rm{ }} = {\rm{ }}2{\rm{ }} \times {\rm{ }}2{\rm{ }} \times {\rm{ }}2{\rm{ }} \times {\rm{ }}2{\rm{ }} \times {\rm{ }}7\)
Prime factor of \(112 = {2^4}{\rm{ \times }}7\)
112 has 10 factors, namely\(1,{\rm{ }}2,{\rm{ }}4,{\rm{ }}7,{\rm{ }}8,{\rm{ }}14,{\rm{ }}16,{\rm{ }}28,{\rm{ }}56{\rm{ }}and{\rm{ }}112\) .
All factors of \(112{\rm{ }} = {\rm{ }}1,{\rm{ }}2,{\rm{ }}4,{\rm{ }}7,{\rm{ }}8,{\rm{ }}14,{\rm{ }}16,{\rm{ }}28,{\rm{ }}56,{\rm{ }}and{\rm{ }}112\)
Factors of 112 in pairs
When we make pairs of factors, the product of the two factors is the given number itself.
Factor pairs of \(112:{\rm{ }}\left( {1 \times 112} \right),{\rm{ }}\left( {2 \times 56} \right),{\rm{ }}\left( {4 \times 28} \right),{\rm{ }}\left( {7 \times 16} \right),{\rm{ }}\left( {8 \times 14} \right)\)
112 factor pairs of \(\left( {1,{\rm{ }}112} \right),{\rm{ }}\left( {2,{\rm{ }}56} \right),{\rm{ }}\left( {4,28} \right),{\rm{ }}\left( {7,{\rm{ }}16} \right),{\rm{ }}\left( {8,14} \right)\)
We know the multiplication property,
\(a{\rm{ }} \times {\rm{ }}b{\rm{ }} = {\rm{ }}b{\rm{ }} \times {\rm{ }}a\)
Pairwise factors of \(112:{\rm{ }}\left( {1,{\rm{ }}112} \right),{\rm{ }}\left( {2,{\rm{ }}56} \right),{\rm{ }}\left( {4,{\rm{ }}28} \right),{\rm{ }}\left( {7,{\rm{ }}16} \right),{\rm{ }}\left( {8,{\rm{ }}14} \right)\)
The divisors of \(112:{\rm{ }}\left( {1,{\rm{ }}112} \right),{\rm{ }}\left( {2,{\rm{ }}56} \right),{\rm{ }}\left( {4,{\rm{ }}28} \right),{\rm{ }}\left( {7,{\rm{ }}16} \right),{\rm{ }}\left( {8,{\rm{ }}14} \right)\) are the same.
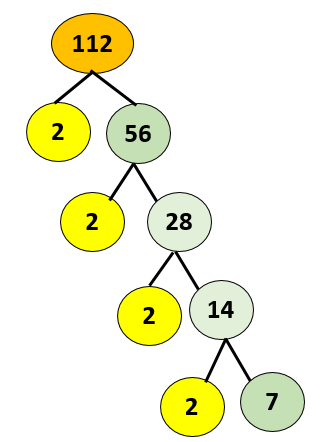
Factor tree of 112
A factor tree is a special graph where we find the factors of a number and then find the factors of those numbers until we can no longer factor them. In the end, all we get are the prime factors of the original numbers.
A factor tree of 112 is a list of prime numbers when multiplied by the original number 112.
\(\begin{array}{*{20}{l}}{112{\rm{ }} = {\rm{ }}2{\rm{ }} \times {\rm{ }}56}\\{56{\rm{ }} = {\rm{ }}2{\rm{ }} \times {\rm{ }}28}\\{28{\rm{ }} = {\rm{ }}2{\rm{ }} \times {\rm{ }}14}\\{14{\rm{ }} = {\rm{ }}2{\rm{ }} \times {\rm{ }}7}\end{array}\)
If we write the multiple it will be \(112{\rm{ }} \times {\rm{ }}2\)
When splitting 56 further and writing it as a multiple of the number, it would be \(28{\rm{ }} \times {\rm{ }}2.\)
When splitting 28 further and writing it as a multiple of the number, it would be \(14{\rm{ }} \times {\rm{ }}2.\)
When splitting 14 further and writing it as a multiple of the number, it would be \(7{\rm{ }} \times {\rm{ }}2.\)
In prime factors the sum of this number is \(2{\rm{ }} \times {\rm{ }}2{\rm{ }} \times {\rm{ }}2{\rm{ }} \times {\rm{ }}2{\rm{ }} \times {\rm{ }}7\).
So,
The factors of 112 are 1, 2, 4, 7, 8, 14, 16, 28, 56 and 112 itself.
Did you know
- Except 0 and 1, every integer has at least two factors: 1 and the number itself.
- The factor of a number is always less than or equal to the number; it can never be greater than the number.112 is not a perfect square..
- 112 is a composite number.
- 112 is an even number.
- 112 is not a perfect square.
Solved example
- Find all the factors of 20.
Step 1: Write down all the numbers from 1 to 20.
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20
Step 2: Now check which of these numbers are divisible by 20 and have no remainder.\(\begin{array}{*{20}{l}}{\;\;\;\;\;\;\;\;\;20/1{\rm{ }} = {\rm{ }}20}\\{\;\;\;\;\;\;\;\;\;20/2{\rm{ }} = {\rm{ }}10}\end{array}\;\;\;\;\;\;\;\;\;20/3{\rm{ }} = {\rm{ }}indivisible\) .
Go ahead and divide 20 by these numbers.
Step 3: The factors of 20 are 1, 2, 4, 5, 10, and 20.
- Find all the factors of 31.
31 is a prime number. The only two numbers that divide 31 are 1 and 31.
So the factors of 31 are 1 and 31.
- Find the prime factors of 144.
As the name suggests, prime factorization is a method of deriving the prime factors of any number. Prime factors are prime numbers. The factors of these numbers are 1 and the numbers themselves. For example, 13 is a prime number because the factors of this number are 1 and 13.
Consider the number 144. Consider first the smallest possible factor, which is 2.
\(144{\rm{ }} = {\rm{ }}2{\rm{ }} \times {\rm{ }}72{\rm{ }} = {\rm{ }}2{\rm{ }} \times {\rm{ }}2{\rm{ }} \times {\rm{ }}36{\rm{ }} = {\rm{ }}2{\rm{ }} \times {\rm{ }}2{\rm{ }} \times {\rm{ }}2{\rm{ }} \times {\rm{ }}18{\rm{ }} = {\rm{ }}2{\rm{ }} \times {\rm{ }}2{\rm{ }} \times {\rm{ }}2{\rm{ }} \times {\rm{ }}2{\rm{ }} \times {\rm{ }}9{\rm{ }} = {\rm{ }}2{\rm{ }} \times {\rm{ }}2{\rm{ }} \times {\rm{ }}2{\rm{ }} \times {\rm{ }}2{\rm{ }} \times {\rm{ }}3{\rm{ }} \times {\rm{ }}3\) So, the prime factors of 144 are 2 and 3 because these factors are prime numbers.
Conclusion
The easiest way to determine the factors of a number is to divide by the smallest prime number with no remainder and continue the process. 112 has more than two factors, namely 1, 2, 4, 7, 8, 14, 16, 28, 56 and 112, so it is a composite number. 112 is an even number, and it is not a perfect square.
Frequently asked question
1. What are the factors of 112?
Since 112 is a composite number, it has more than 2 factors, so the factors of 112 are 1, 2, 4, 7, 8, 14, 16, 28, 56, and 112.
2. What is the prime factorization of 112?
Prime factorization of 112, we can write \(112 = \;2{\rm{ }} \times {\rm{ }}2{\rm{ }} \times {\rm{ }}2{\rm{ }} \times {\rm{ }}2{\rm{ }} \times \;7\)
3. What are the negative pair factors of 112?
The negative pair factors of 112 are \(\left( { – 1,{\rm{ }} – 112} \right),{\rm{ }}\left( { – 2,{\rm{ }} – 56} \right),{\rm{ }}\left( { – 4,{\rm{ }} – 28} \right),{\rm{ }}\left( { – 7,{\rm{ }} – 16} \right)\) and \(( – 8, – 14).\)

