Introduction
No matter how many sides there are in a polygon, the sum of all exterior angles is \({\bf{360}}^\circ \), and the sum of all internal angles is \(\;\left( {{\bf{n}} – {\bf{2}}} \right){\bf{180}}^\circ \) given that the number of sides is n.
Shapes are \(2 – \) dimensional and \(3 – \) dimensional; we have all seen them. A shape is also a polygon. A two-dimensional form having at least three sides is called a polygon. There might be four, five, or more sides. There are two types of polygons: regular polygons and irregular polygons. The sum of all external angles created in the polygon is the sum of measurements of the exterior angles. We shall explore exterior angles and the total of all exterior angles of a polygon in this subject.
Polygons
Polygons are \(2 – \) dimensional, plane figures with straight edges joining n points on a plane. The polygons are divided into two main sub-categories, i.e., Convex Polygons and Concave Polygons.
Concave Polygons

In these types of polygons, at least one of the diagonals passes outside of the polygon and at least one of the vertex is pointing inside the polygon, i.e., has an angle greater than \(180^\circ \). Stars are one of the most common examples of concave polygons.
Convex Polygons
Convex polygons are the normal polygons, that have all the interior angles less than \(180^\circ \) , all the diagonals are always contained within the polygon.

Few of the most common examples of convex polygons are triangles and squares. Learn more about convex polygons in Class 6 Mathematics Video in Lesson no 14 Curves, Polygon.
Convex polygons are divided into \(2\) categories,
- Regular polygons: These are the convex polygons that have all their sides of equal length, and the measure of each interior angle is equal.
- Irregular polygons: These are the convex polygons that are not regular, i.e., their sides and angles are not all of equal measure.
Exterior angles
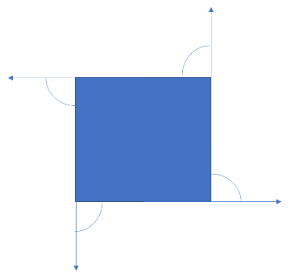
The external angle is the angle created outside of a polygon when one of its sides is expanded. It is created by the expanded side and the side next to it.
Properties of Exterior Angles of Polygons
Consider the many characteristics of the exterior angle of a hexagon, a polygon, for example. The attributes listed below provide information on the exterior angles:
- They are created outside of the specified figure.
- The internal and exterior angles that are created by the expanded side and the neighboring side are always added together.
- A regular polygon’s exterior angles are always equal to one another.
Sum of Exterior Angles of a Polygon: Geometrical Proof
Let’s take an example of hexagon, marking the vertices \(ABCDEF\) , so let’s move on the edge of this hexagon. Starting from \(A\) we move in a straight line, no turns happen until we reach vertex \(B\), where we turn slightly, the measure of the exterior angle at \(B\) , and once again move in a straight line until vertex \(C\) , we rinse and repeat this process until we are at our final stretch, i.e., edge \(FA\) . We have turned to the sum of all angles except A. Now at A we will turn once again and face the direction we started in, this gives us that we have turned a complete circle, i.e., 360, by rotating through each angle one by one.
\(A + B + C + D + E + F = 360^\circ \)
Sum of Exterior angles =360°
Sum of Exterior Angles of a Polygon: Algebraic Proof
Let us consider a \(n – sided\) polygon. By Interior angle property we know that the sum of all interior angles is given by, \[180^\circ \times (n – 2)\]
Also, we know that each exterior angle forms a linear pair with the corresponding interior angle, thus the sum of all interior angles and the sum of all exterior angles should be equal to the sum of all the linear pairs formed.
180(n-2)+Sum of Exterior Angles=180n
Sum of Exteriror angles = 180n-180(n-2)
\( = 180n – 180n + 360\)
\( = 360^\circ \)
Summary
We examined the following salient characteristics in the aforementioned study:
Any sort of polygon’s exterior angles add up to \(360\).
Any form of polygon’s internal angles add up to (180\left( {n – 2} \right)\) .
A regular polygon’s exterior angles have a value of \(360/n\) .
A regular polygon’s internal angles are determined using the formula \(\frac{{180\left( {n – 2} \right)}}{n}\) .
Online Tuition for Class 6 Maths
FAQs
1. What is the name of a polygon with \({\bf{12}}\) sides?
Ans. A polygon with \(12\) sides is known as a Dodecagon.
2. What is the measure of interior angles of a regular polygon of \({\bf{7}}\) sides?
Ans. The measure for interior angles of a n sided polygon is given by, \[\frac{{180\left( {n – 2} \right)}}{n}\] , substituting \(n = 7\) , we have,
\[\frac{{180\left( {7 – 2} \right)}}{7} = \frac{{900}}{7}\;\; \approx 128.57^\circ \]
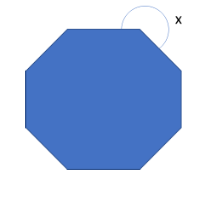
3. What is the measure of x in the following image?
Ans. In the given image, the angle x is the reflex angle of the interior angle of a regular octagon, thus we will find the interior angle of the octagon and subtract it from \(360^\circ \)
Interior angle\( = \frac{{180\left( {n – 2} \right)}}{n}\)
Substituting \(n = 8\) ,
\(\begin{array}{*{20}{l}}{ = \frac{{180 \times 6}}{8} = 135^\circ }\\\;\end{array}\)
The reflex of this would be,
\[x = 360 – 135 = 225^\circ \]

